(點選上方公眾號,可快速關註)
來源:笨狐狸,
blog.csdn.net/liweisnake/article/details/69253206
本章我們來討論一種最終一致的演演算法,paxos演演算法。
paxos演演算法是由大牛lamport發明的,關於paxos演演算法有很多趣事。比如lamport論文最初由故事描述來引入演演算法,以至於那班習慣數學公式的評委將該論文打回,導致該論文延誤了8年才公開發表。另外,google的chubby的作者Mike Burrows說過,世界上只有一種一致性演演算法,那就是paxos。
兩將軍問題
為了引入該演演算法,首先提出一種場景,即兩將軍問題(見文獻1):
有兩支軍隊,它們分別有一位將軍領導,現在準備攻擊一座修築了防禦工事的城市。這兩支軍隊都駐紮在那座城市的附近,分佔一座山頭。一道山谷把兩座山分隔開來,並且兩位將軍唯一的通訊方式就是派各自的信使來往於山谷兩邊。不幸的是,這個山谷已經被那座城市的保衛者佔領,並且存在一種可能,那就是任何被派出的信使透過山谷是會被捕。 請註意,雖然兩位將軍已經就攻擊那座城市達成共識,但在他們各自佔領山頭陣地之前,並沒有就進攻時間達成共識。兩位將軍必須讓自己的軍隊同時進攻城市才能取得成功。因此,他們必須互相溝通,以確定一個時間來攻擊,並同意就在那時攻擊。如果只有一個將軍進行攻擊,那麼這將是一個災難性的失敗。
兩將軍問題本質上就是通訊被篡改時能否解決一致性問題。這個問題已經被很多人證明不能。(見文獻1)。因而由此推及的拜占庭將軍問題(多將軍問題)也同樣不能被解決。
PAXOS演演算法
一個叫做Paxos的希臘城邦,這個島按照議會民主制的政治樣式制訂法律,但是沒有人願意將自己的全部時間和精力放在這種事情上。所以無論是議員,議長或者傳遞紙條的服務員都不能承諾別人需要時一定會出現,也無法承諾批准決議或者傳遞訊息的時間。但是這裡假設沒有拜占庭將軍問題(Byzantine failure,即雖然有可能一個訊息被傳遞了兩次,但是絕對不會出現錯誤的訊息);只要等待足夠的時間,訊息就會被傳到。另外,Paxos島上的議員是不會反對其他議員提出的決議的。
這裡不再贅述演演算法的推導及證明過程,參考文獻2和3。這裡簡單描述下演算法理解。
基本思想也是兩階段提交。但是與兩階段目的不同。
1. 第一階段主要目的是選出提案編號最大的proposer。
其描述如下,所有的proposer向超過半數的acceptor提出編號為n的提案,acceptor收到編號為n的請求,會出現兩種情況
a. 編號n大於所有acceptor之前已經批准過的proposal的最大編號及內容m。acceptor同意該proposal,響應[n, m]回proposer,並且承諾今後不再批准任何編號小於n的提案。
b. 編號n小於acceptor之前批准過的任意proposal的編號。acceptor拒絕該proposal。
2. 第二階段嘗試對某一proposal達成一致。
proposer收到超過半數的acceptor傳回的響應,proposer就會將響應的最大編號[n, m]對應的提案提交到acceptor要求acceptor批准該提案。
acceptor收到最大編號[n, m]的提案,也分為兩種情況
a. 未響應過編號大於n的prepare請求。透過該提案。
b. 已響應過編號大於n的prepare請求。拒絕該提案。
整個演演算法錶面上並不難理解,難在實現細節的難易程度和各種異常情況的推導及考慮。如果對上述演演算法有理解困難的,參考文獻4和文獻5的例子,其中文獻5更容易理解,這裡 把他的圖貼出來,實際過程就不再重覆贅述了。
兩個參謀先後提議的場景:

兩個參謀交叉提議的場景:
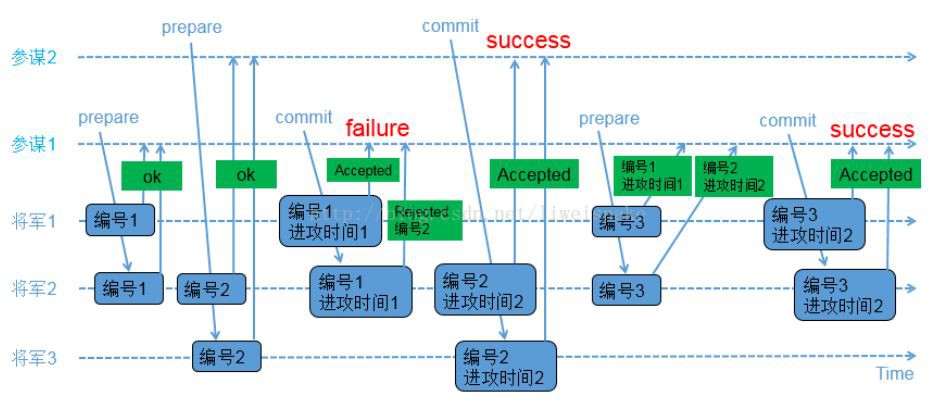
需要註意的是參謀1在失敗時再次發起請求的過程。
這裡著重強調幾個重點:
-
演演算法描述裡有好幾個地方要求投票必須超過半數,這個超過半數恰恰是保證一致的一個必要條件;
-
演演算法裡也有多處要求只選擇編號最大的,這種選擇編號最大的方式,是一種最為簡單經濟的達成共識的方法,能夠快速在多個衝突中找到一個突破口;
-
paxos演演算法的關鍵是,如果一個值m被選中了,那麼必須保證更高的proposal其值也為m;
-
註意第一階段比較的是已經批准過的proposal的最大編號,而第二階段比較的是prepare請求。即第一階段比較的是第二階段的結果,而第二階段比較的是第一階段的結果,看似很繞,實際上正好是隔離了階段外的保證,進入第一階段的我要保證他是新的開始,跟上一階段沒啥關係,而進入第二階段的我要保證他是從前面階段來的,而不是新起的一個階段,有點像是隔離鎖,鎖住了階段一到階段二這個過程。
參考閱讀
-
分散式系統的事務處理
http://coolshell.cn/articles/10910.html
-
paxos wiki
https://en.wikipedia.org/wiki/Paxos_(computer_science)
-
paxos維基
https://zh.wikipedia.org/wiki/Paxos%E7%AE%97%E6%B3%95
-
paxos演演算法例子
https://www.zhihu.com/question/19787937/answer/107750652
-
paxos演演算法例子2*
http://iunknown.iteye.com/blog/2246484?from=message&isappinstalled;=0
-
Paxos演演算法1-演演算法形成理論
http://blog.csdn.net/chen77716/article/details/6166675
看完本文有收穫?請轉發分享給更多人
關註「ImportNew」,提升Java技能

 知識星球
知識星球