黎曼猜想仍舊，素數依然孤獨

作者：老喻在加

來源：孤獨大腦（ID：lonelybrain）

01

“舉世矚目”這類事，在地球上註定日漸稀缺。世界越來越平，而作為個體的人類，則越來越平庸。

這就是為什麼“黎曼猜想”將被驗證的訊息，在全球引起如此關註。

然而，偉大時刻並未降臨。89歲的阿蒂亞沒能創造奇跡。這不令人意外，歷史上幾乎沒有人能在這個年齡，取得數學上的突破。

《新科學家》聯絡了許多數學家，請他們對阿蒂亞的證明發表評論，但他們都拒絕了。老人家近年來發表了許多論文，提出了令人矚目的主張，但迄今未能說服他的同行。

就像牛頓後來沉迷於煉金術，愛因斯坦執著於統一場，阿蒂亞之所為，在很多人眼中彷彿一個笑話。

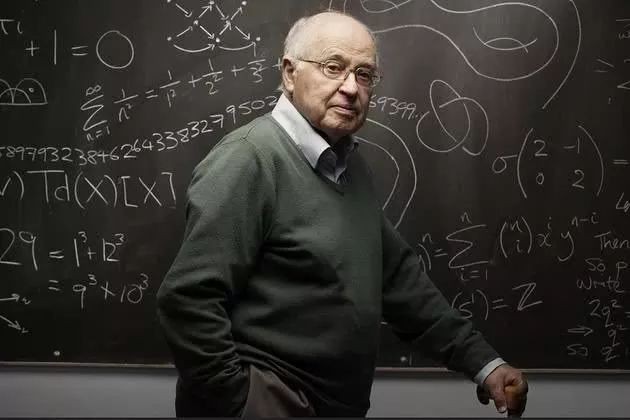
邁克爾·阿蒂亞爵士，被譽為當代最偉大的數學家之一。他拿過菲爾茲獎、科普利獎章、阿貝爾獎，擁有幾乎所有的榮耀。他根本不需做任何事情來證明自己，相反，他的冒險破壞了一世英名的圓滿。

阿蒂亞說： “我已得到自己所需的全部獎項， 還有什麼可失去的？ 這就是我為什麼會冒年輕研究者不準備冒的險。”

我眼中的邁克爾·阿蒂亞爵士，正是這樣的英雄。

在我們身邊，甚至在我們的想象中，這樣的人已經絕跡了。

另一方面，據蔡天新老師微博寫道，2018年阿蒂亞結婚63年的妻子、最親愛的弟弟相繼去世；此前，他的長子和長媳、侄兒在徒步旅行時莫名死去。黎曼猜想對他而言是最大的精神安慰。

讓我改寫西蒙.辛格在《費馬大定理》裡的一段話：

“黎曼猜想”的故事與數學的歷史有著千絲萬縷的聯絡，觸及到數論中所有重大的課題。它對於“是什麼推動著數學發展”，或許更重要的“是什麼激勵著數學家們”提供了一個獨特的見解。

“黎曼猜想”是一個充滿勇氣、欺詐、狡猾和悲慘的英雄傳奇的核心，牽涉到數學王國中所有的最偉大的英雄。

當我將費馬大定理換成黎曼猜想，原句幾乎完全成立。 

02

波恩哈德·黎曼，1872年出生於漢諾威王國一個貧困不堪的牧師家庭，性格羞澀並患有肺病。他一無所有，除了在數學領域的天賦。

與費馬大定理不同，黎曼猜想很難用大眾理解的表述來呈現。

作為數學中最著名的未決問題，黎曼假設有若干種等價的表達形式，其中一種涉及素數定理給出的估計的精度。高爾斯在《數學》（牛津通識讀本）裡介紹說，素數定理告訴我們在某數附近素數的近似密度。

素數是大於1且不能被其他整數——1和自身顯然除外——整除的整數。自從古希臘時期以來，素數就一直困擾著數學家們，因為它們錶面上多多少少是隨機分佈的，但又並非全然隨機。從沒有人找出一種簡單的規則，能夠告訴我們第 n個素數是多少。

和小素數比起來，大素數的出現越來越稀疏。但它們稀少到何種具體程度？如果你在 1 000 001和 1 010 000之間隨機取一數，那麼這個數有多大的機會是素數？換言之， 1 000 000附近的素數“密度”是多大？它是極其小還是僅僅比較小？

有許多關於素數的著名問題。

例如，哥德巴赫猜想斷言，任意大於4的偶數都可以表示為兩個奇素數之和。這個猜想看起來比維諾格拉多夫所解答的三素數猜想要難得多。

還有孿生素數猜想，它聲稱有無窮對相距為 2的素數，諸如17與19，137與 139，儘管越來越稀少。

素數在自然數中的分佈問題在純粹數學和應用數學上都很重要。素數在自然數中的分佈並沒有簡單的規律。黎曼發現素數出現的頻率與黎曼ζ函式緊密相關。

1901年Helge von Koch指出，黎曼猜想與強條件的素數定理等價。現在已經驗證了最初的1,500,000,000個素數對這個定理都成立。但是是否所有的解對此定理都成立，至今尚無人給出證明。

黎曼猜想所以被認為是當代數學中一個重要的問題，主要是因為很多深入和重要的數學和物理結果都能在它成立的大前提下得到證明。

黎曼猜想是20世紀數學家應當努力解決的23個數學問題，也是克雷數學研究所懸賞100萬美元的千禧年七大數學難題之一。

試圖證明黎曼猜想的努力， 堪稱是一場天才的盛宴（或絞殺場）。例如影片《美麗心靈》的主角、 美國數學家納什，極可能是因為黎曼猜想而導致精神分裂症。

03

證明黎曼猜想有什麼用嗎？

按照我們的世俗標準，基本沒用。

傳說中的“區塊鏈和加密貨幣將被摧毀”，並不會發生。

目前加密貨幣市場上的加密貨幣，幾乎都是由雜湊運算函式和數字加密證書兩方面構成的。

雜湊演演算法和素數無關。加密演演算法，如果是橢圓曲線數字簽名，和素數分解沒有特別大的關係；如果是非對稱加密，實際上是在做素數分解，和黎曼猜想的找素數關係不大。

因此，市場上的加密貨幣幾乎不會受到太大影響，比如比特幣使用的是專門經過修改的橢圓曲線加密，而其他虛擬貨幣使用的加密演演算法，幾乎很少會使用RSA加密演演算法，有的則是會在RSA演演算法基礎上再加一層加密演演算法，作雙重保險。

所以，黎曼猜想對公鑰密碼沒有直接的威脅，對區塊鏈的安全也沒有影響。

有業內人士說：從應用角度來看，“黎曼猜想的命題是完整的，只要認為它為真就可以拿來用，而不需要一定等到‘證明瞭為真’才可以用。而且，從來沒聽說過針對任何領域的任何攻擊方法裡，黎曼定理起到了重要作用。” 

《黎曼猜想漫談》作者盧昌海說：

……並沒有哪一種網際網路加密方式是以黎曼猜想的不成立為前提， 從而會因黎曼猜想的成立而破滅的。 退一步說， 哪怕有這樣的加密方式， 那它的破滅與否也只是依賴於黎曼猜想的成立與否， 而非證明與否——證明只是對破滅的確認， 並不締造破滅的事實。

黎曼猜想被稱為最重要的數學猜想， 原因是：

1. 它跟其它數學命題之間有著千絲萬縷的聯絡。 在今天的數學文獻中已經有一千條以上的數學命題是以黎曼猜想 (或其推廣形式) 的成立為前提的。 

2. 黎曼猜想與數論中的素數分佈問題有著密切關係。 而數論是數學中一個極重要的傳統分支， 被德國數學家高斯稱為是 “數學的皇后”。 素數分佈問題則又是數論中極重要的傳統課題。 

3. 一個數學猜想的重要性還有一個衡量標準， 那就是在研究該猜想的過程中能否產生出一些對數學的其它方面有貢獻的結果。 

4. 黎曼猜想的重要性甚至越出了純數學的範圍， 而 “侵入” 到了物理學的領地上。 20 世紀 70 年代初， 人們發現與黎曼猜想有關的某些研究， 居然跟某些非常複雜的物理現象有著顯著關聯。 這種關聯的原因直到今天也還是一個謎。

04

“數學是上帝書寫宇宙的語言 ！ ”

現代科學發展的基石就是數學 ，甚至一門學科與數學聯絡的緊密程度可以代表該學科的發展水平 。

黃徵在《數學沉思錄》的序言裡談及：

“究竟什麼是數學？”

• 數學王國是一個獨立存在於宇宙之中 ，我們僅僅只能窺視一角的真實世界 ？

• 數學的發展可以視為人類一種純粹的思維上的智力活動 ？

英國物理學家詹姆斯 ·瓊斯曾指出 ：

 “宇宙似乎是由一位理論數學家設計的 。”

數學似乎不僅是描述和解釋整個宇宙最有效的工具 ，而且可以用來解釋最複雜的人類活動 。

Livio寫道：

今天 ，無論是物理學家試圖創立一種關於宇宙的新理論 ，股票市場分析員苦苦思索以預測下一輪股市暴跌 ，神經生物學家構建大腦功能模型 ，還是軍事情報專家最佳化各種軍事資源配置 ，他們都要使用數學 。而且 ，即使他們在形式上發展出了數學的不同分支 ，在基礎研究中他們依然需要求助於通用 、一致的數學基本理論 。

是什麼賦予數學如此令人難以置信的力量 ？

正如愛因斯坦曾經驚嘆的 ：

 “數學 ，這個獨立於人類經驗存在的人類思維產物 ，怎麼會如此完美地與物理現實中的物質相一致 ？ ”

諾貝爾物理學獎得主尤金 ·維格納有同樣的疑惑：

數學語言適於表達物理法則 ，這種神奇是上天賜予我們的絕妙禮物 。事實上我們並未真正理解這份禮物 ，同時也受之有愧 。我們應當感謝這份禮物 ，希望在未來的研究中它仍然有效 ，而且繼續擴充套件以拓展人類認識 ，無論這是好是壞 ，也無論這帶給我們的是歡樂還是困惑 。

著名的牛津數學物理學家羅傑 ·彭羅斯意識到 ，人類周圍並不是僅有 1個世界 ，而應該有 3個神秘世界 ：

1. 意識感知的世界

這是我們所有精神影像的家園 ，包括我們看到自己孩子笑臉時的歡欣愉悅 、欣賞落日餘暉壯美景色時的心曠神怡 ，或者觀察怵目驚心的戰爭場面時的恐懼和憎惡 。在這個世界中還包括愛 、忌妒 、偏見 、害怕 ，以及我們欣賞音樂 、聞到美食時的感覺 。

2. 物理現實的世界

就是我們日常所提到的物理現實世界 ，包括鮮花 、阿斯匹林藥片 、白雲 、噴氣式飛機 ，還有星系 、行星 、原子 、狒狒的心臟 、人類的大腦 。

3. 數學形式的柏拉圖世界 

這裡是數學的家園 ，有自然數 1 、 2 、 3 、 4 … … ，歐幾裡得幾何學所有圖形和定理 、牛頓運動定律 、弦論 、突變論 ，以及研究股票市場行為的數學模型等 。

彭羅斯還觀察到了這 3個世界之間神秘相聯的 3種現象 。

• 現象1：物理世界的執行似乎遵循著一定的法則 ，而這些法則真實存在於數學世界中 。

• 現象2：人類洞察性思維本身 ——我們主觀認知能力的源泉 ——似乎來自於物理世界 。

• 現象3：這 3個世界神秘地聯到一起 ，形成了一個閉合的圓 。透過發現或創造抽象的數學公式和概念 ，並將它們清晰地表達出來 ，洞察性思維才得以奇跡般地進入數學王國之中 。

例如，開普勒和牛頓發現了太陽系行星執行軌道是橢圓形的 ，而古希臘數學家門奈赫莫斯兩千年前就已經研究過這個曲線了 。

又如，黎曼在1854年的一次經典演講中概括了幾門新興幾何學的主要內容 ，後來成為愛因斯坦解釋宇宙結構時所必需的工具 。

數學家丘成桐談到：

黎曼還是第一位引入獨立於歐氏幾何的空間概念的學者。他用坐標來測量長度，面積和曲率等幾何量。他希望這些值與坐標的選取無關，這叫做等效原理，是愛因斯坦後來用作推導他的場方程的一個基本假設。愛因斯坦受到黎曼工作的深刻影響。

05

英國數學家哈代回憶印度數學家拉馬努金時談到，某次他去醫院看望拉馬努金，提到路上搭乘的出租車的車牌號為 1729，並無特殊之處。

拉馬努金說：“你錯了。實際上，這是能以兩種方式表示為兩數立方和的最小自然數。”

昨天，在邁克爾·阿蒂亞爵士的演講PPT裡，出現了拉馬努金。

2016年4月，著名投資人尤里·米爾納在自己家中舉行了一場小規模的晚宴，到場嘉賓包括Google CEO皮查伊、Google創始人布林、Facebook創始人兼CEO扎克伯格及其他數十位矽谷領袖。晚宴上，米爾納放映了一部導演馬修·布朗最新拍攝的傳記體電影——《知無涯者》。影片講述了印度傳奇數學家拉馬努金的一生。

據說，扎克伯格等人是紅著眼眶走出來的。他們當即宣佈將聯手成立一項新基金，以致敬及紀念拉馬努金。

1913年1月31日，英國劍橋大學36歲的著名數學家G·H·哈代收到了一摞從印度寄來的手稿，並附介紹函一封：

尊敬的先生，謹自我介紹如下：

我是馬德拉斯港務信託處的一名會計師，年薪不過20英鎊……我在發散級數理論上取得了一些驚人的進展，破解了由來已久的素數分佈問題……如果您認為我的定理有價值，我會將它們發表……我只是個無名小卒，您提出的任何建議都將為我所珍視。

冒昧打擾，還望見諒。

S·拉馬努金敬啟。

手稿裡有莫名其妙、看似荒誕的公式。也有實驗性質的數學研究方法論，更不乏整頁整頁的怪異公式：

看完手稿，以為遇到騙子的哈代驚呼：“這些定理徹底把我打敗了，真是見所未見，聞所未聞！”

哈代認為這些定理“一定是成立的，因為沒有哪個人類的想象力可以強大到憑空把它們造出來。” 

當時他們還不知道，這個印度窮小子拉馬努金連正規的高等數學教育都沒受過。

06

據DeepTech深科技報道：

阿蒂亞爵士提出了對黎曼猜想證明方法的一個簡單思路。其靈感來源於他提出精細結構常數的推演，這是一個物理學上長期存在的數學問題。這一推演過程結合了馮·諾依曼的運算元理論及希策布魯赫創立並證明的代數簇黎曼-羅赫定理，還應用了Todd函式參與計算，而這個函式將是證明黎曼猜想的核心。

一些學者對他的推演過程存疑，同樣，也有學者對此次黎曼猜想的證明過程質疑。有一些學者認為，阿蒂亞爵士的思路或為後續黎曼猜想證明提供了一種新思路。

阿蒂亞爵士並未做出證明的全部工作，其思路基於一個物理上未被完全證明的常數。

阿蒂亞爵士曾表示：為什麼這麼老了仍做研究？因為自己受一種從未離開過自己的激情所驅使：

 “我已從事數學研究 70 年， 我無法停下。”

在演講的最後，阿蒂亞向數學界的後輩們提出了四點建議。

1. 要運用如今最強大的工具，這裡的工具不僅限於數學工具，還包括超級計算機甚至是量子計算機，還有其他領域例如物理學界、邏輯學界等的工具；

2. 借鑒其他著名猜想，不管是證明瞭的還是未證明的；

3. 需要判斷哪些難題是能夠高效率完成計算的；

4. RH（黎曼假設）已經是很難的一個猜想了，證明出其一部分就已經很了不起了，希望數學界的後輩們能權衡一下，哪些黎曼猜想的方面是我們有時間完成的，做出決定就無悔地去做吧！

07

中國人對自己的“數學好”，有迷之自信。事實上，我家兩個在加拿大接受教育的孩子，對比國內同齡小學生，在數學上的進度確實有差距。中國的奧數似乎很厲害，中國孩子花在做數學題上的平均時間，可能也是世界領先。

但為什麼我們極少出數學家？如果沒記錯的話，這些年似乎只湧現了一位流落美國的張益唐。

這個話題極為龐大，我想借Livio之筆，簡單談及如下：

數學發展的這幅素描，儘管簡略，但卻表明數學的生命力正是根植於養育她的文明的社會生活之中。

……

由於古希臘數學家強調嚴密的推理以及由此得出的結論，因此他們所關心的並不是這些成果的實用性，而是教育人們去進行抽象的推理，和激發人們對理想與美的追求。

因此，看到這個時代具有後世很難超越的優美文學，極端理性化的哲學，以及理想化的建築與雕刻，也就不足為奇了。

公元前 221年被突然闖入的羅馬士兵殺害了，當時大師在研究畫在沙盤中的幾何圖形。對此， A· N·懷特海說過：

阿基米德死於一個羅馬士兵之手，是世界發生頭等重要變化的一個標誌：愛好抽象科學、擅長推理的古希臘在歐洲的霸主地位，被重實用的羅馬取代了。

L·比肯斯菲爾德（ Lord Beaconsfield）在他的一部小說中，曾把重實用的人稱為重覆其先輩錯誤的人。

羅馬是一個偉大的民族，但是他們卻由於只重實用導致了創造性的缺乏而受到了人們的指責。他們沒有發展其祖先的知識，他們所有的進步都侷限於工程技術的細枝末節。

他們並不是那種能夠提出新觀點的夢想家，這些新觀點能給人以更好地主宰自然界的力量。沒有一個羅馬人因為沉湎於數學圖形而喪命。

當然，另外一方面，西塞羅則誇耀自己的同胞，不是像希臘人一樣的夢想家，而是把他們的數學研究派上實際用場的人。

Livio繼續寫道：

註重實用的羅馬帝國，將其精力用於權術和征服外邦。為迎接軍隊勝利歸來的拱形的凱旋門，也許是羅馬帝國的最好象徵，但它們不是顯得優雅得體，而是顯得毫無生氣。

羅馬最突出的特徵也許是麻木不仁，羅馬人幾乎沒有真正的獨創精神。

最後

哈代說：即使埃斯庫羅斯被人們遺忘了，阿基米德仍會被人們記住，因為語言文字會消亡而數學概念卻不會。“不朽”可能是個缺乏理智的用詞，但是或許數學家最有機會享用它，無論它意味著什麼。

不朽，與我等凡人無關。

但，數學與這個物理世界一起，是上帝庇護我們的工具。

我從來不是一個好學生，成年後倒是熱衷於做題，在朋友圈裡以解題快著稱。這個愛好對我投資、做公司，未必有何裨益，但有助於我在偶爾給孩子輔導數學時找到樂趣。

義大利粒子物理學博士保羅·喬爾達諾，曾經寫過一本《質數的孤獨》：

馬蒂亞是一個年輕的數學天才，他相信自己是質數中的一個，而中學同學愛麗絲正是他的孿生質數。他們都有痛苦的過往，同樣孤獨，同樣無法拉近和其他人之間的距離。

從少年到成年，他們的生命不斷交叉，努力消除存在於彼此間障礙，相互影響又彼此分離，就像孿生質數，彼此相近卻永遠無法靠近。

（這裡的孿生質數，就是前面提過的孿生素數。廣泛來說，質數就是素數。）

人類在宇宙間是無盡孤獨的。但我總覺得，這是上帝為我們設計的最佳遊戲。

假如素數的分佈不是那麼神秘，假如沒有黎曼們的孤獨探索，假如沒有阿蒂亞的勇戰風車，假如沒有這類對意義和公式的追求，人類可能早被虛無的黑洞吞沒了。

加繆在《西西弗斯神話》中闡釋了自己的荒謬哲學，即人在面對一個沒有上帝以及永恆的真理或價值的世界時對意義、統一性以及明晰性的無益探求。

書中最後一章，對人們生活的荒謬性與反覆推石頭上山的西西弗斯的狀況進行了比較。

在書的最後，作者總結性地說：

“邁向高處的掙扎足夠填充一個人的心靈。人們應當想象西西弗斯是快樂的。”