本文主要介紹譜歸一化這項技術，詳細論文參考 Spectral Normalization for Generative Adversarial Networks。

本文主要對論文中的基礎知識和遺漏的細節做出補充，以便於更好地理解譜歸一化。部分內容參考並整合瞭如下兩篇部落格。

http://kaiz.xyz/blog/posts/spectral-norm/

 

https://christiancosgrove.com/blog/2018/01/04/spectral-normalization-explained.html

Lipschitz Continuity

在 GAN 中，假設我們有一個判別器 D: I→R，其中 I 是影象空間。如果判別器是 K-Lipschitz continuous 的，那麼對影象空間中的任意 x 和 y，有：

其中 || · || 為 L2 norm，如果 K 取到最小值，那麼 K 被稱為 Lipschitz constant。 

直觀地來說，Lipschitz 條件限制了函式變化的劇烈程度，即函式的梯度。在一維空間中，很容易看出 y=sin(x) 是 1-Lipschitz 的，它的最大斜率是 1。 

那麼，為什麼要使判別器函式具有 Lipschitz continuity 呢？Wasserstein GAN 提出了用 wasserstein 距離取代之前的 KL 散度或者 JS 散度，作為 GAN 判別器的損失函式：

其中 Pr 和 Pg 分別為真實資料和生成資料的分佈函式，Wasserstein 距離衡量了這兩個分佈函式的差異性。

直觀地理解，就是根據這兩個分佈函式分別生成一堆資料 x1, x2, … , xn 和另一堆資料 y1, y2, … , yn，然後計算這兩堆資料之間的距離。距離的演演算法是找到一種一一對應的配對方案 γ~∏(Pr, Pg)，把 xi 移動到 yj，求總移動距離的最小值。

由於在 GAN 中， Pr 和 Pg 都沒有顯式的運算式，只能是從裡面不停地取樣，所以不可能找到這樣的 γ，無法直接最佳化公式 (2) 。W-GAN 的做法是根據 Kantorovich-Rubinstein duality，將公式 (2) 轉化成公式 (3)，過程詳見以下連結：

https://vincentherrmann.github.io/blog/wasserstein/

其中 f 即為判別器函式。只有當判別器函式滿足 1-Lipschitz 約束時，(2) 才能轉化為 (3)。除此之外，正如上文所說，Lipschitz continuous 的函式的梯度上界被限制，因此函式更平滑，在神經網路的最佳化過程中，引數變化也會更穩定，不容易出現梯度爆炸，因此 Lipschitz continuity 是一個很好的性質。 

為了讓判別器函式滿足 1-Lipschitz continuity，W-GAN 和之後的 W-GAN GP 分別採用了 weight-clipping 和 gradient penalty 來約束判別器引數。這裡的譜歸一化，則是另一種讓函式滿足 1-Lipschitz continuity 的方式。

矩陣的Lipschitz Continuity

眾所周知，矩陣的乘法是線性對映。對線性對映來說，如果它在零點處是 K-Lipschitz 的，那麼它在整個定義域上都是 K-Lipschitz 的。

想象一條過零點的直線，它的斜率是固定的，只要它上面任何一點是 K-Lipschitz 的，那麼它上面所有點都是 K-Lipschitz 的。因此，對矩陣來說，它滿足 K-Lipschitz 的充要條件是：

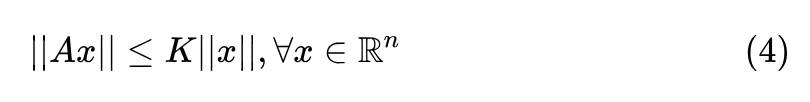
對其做如下變換：

其中 表示兩個向量的內積。由於矩陣是半正定矩陣，它的所有特徵值均為非負。我們假設它的特徵向量構成的基底為 v1, v2,…, vn，對應的特徵值為 λ1, λ2,…, λn，令 x=x1·v1+x2·v2+ … +xn·vn。那麼，公式 (5) 的左半部分可以轉化為：

要使公式 (6) 對任意 xi 恆成立，且 λi 非負，則必有。若 λ1 為最大的特徵值，只需要滿足，這裡即為矩陣 A 的 spectral norm。 

綜上所述，對映滿足 K-Lipschitz 連續，K 的最小值為。那麼，要想讓矩陣 A 滿足 1-Lipschitz 連續，只需要在 A 的所有元素上同時除以即可（觀察公式 (4) 左側是線性對映）。 

透過上面的討論，我們得出了這樣的結論：矩陣 A 除以它的 spectral norm（最大特徵值的開根號）可以使其具有 1-Lipschitz continuity。

矩陣的奇異值分解

上文提到的矩陣的 spectral norm 的另一個稱呼是矩陣的最大奇異值。回顧矩陣的 SVD 分解： 

矩陣存在這樣的一種分解：

其中： 

• U 是一個 m × m 的單位正交基矩陣 

• Σ 是一個 m × n 的對角陣，對角線上的元素為奇異值，非對角線上的元素為 0 

• V 是一個 n × n 的單位正交基矩陣

▲ SVD分解

由於 U 和 V 都是單位正交基，因此可以把矩陣乘以向量分成三步：旋轉，拉伸，旋轉。一前一後的兩步旋轉不改變向量的模長，唯一改變向量模長的是中間的拉伸，即與 Σ 相乘的那一步。而矩陣的 Lipschitz continuity 關心的正是矩陣對向量模長的改變，不關心旋轉。

因此，只需要研究中間的 Σ 即可。而 Σ 又是一個對角矩陣，因此，它對向量的模長拉長的最大值，就是對角線上的元素的最大值。也就是說，矩陣的最大奇異值即為它的 spectral norm。 

根據公式 (7) ，以及 SVD 分解中 U 和 V 都是單位正交基，單位正交基的轉置乘以它本身為單位矩陣，有：

因此，只需要求出的最大特徵值，再開根號，就求出了矩陣的最大奇異值，也就是矩陣的 spectral norm，和上一小節的推導殊途同歸。

神經網路的Spectral Norm

對於複合函式，我們有這樣的定理：

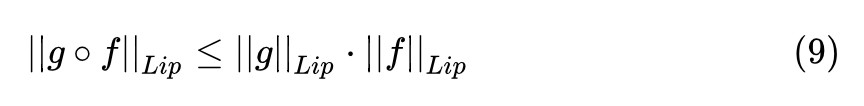
而多層神經網路，正是多個複合函式巢狀的操作。最常見的巢狀是：一層摺積，一層啟用函式，再一層摺積，再一層啟用函式，這樣層層包裹起來。

啟用函式通常選取的 ReLU，Leaky ReLU 都是 1-Lipschitz 的，帶入到 (9) 中相乘不影響總體的 Lipschitz constant，我們只需要保證摺積的部分是 1-Lipschitz continuous 的，就可以保證整個神經網路都是 1-Lipschitz continuous 的。 

而在影象上每個位置的摺積操作，正好可以看成是一個矩陣乘法。因此，我們只需要約束各層摺積核的引數 W，使它是 1-Lipschitz continuous 的，就可以滿足整個神經網路的 1-Lipschitz continuity。

我們已經知道，想讓矩陣滿足 1-Lipschitz continuous，只需要讓它所有元素同時除以它的最大奇異值，或者說是它的 spectural norm。因此，下一步的問題是如何計算 W 的最大奇異值。 

對大矩陣做 SVD 分解運算量很大，我們不希望在最佳化神經網路的過程中，每步都對摺積核矩陣做一次 SVD 分解。一個近似的解決方案是 power iteration 演演算法。

Power Iteration

Power iteration 是用來近似計算矩陣最大的特徵值（dominant eigenvalue 主特徵值）和其對應的特徵向量（主特徵向量）的。 

假設矩陣 A 是一個 n × n 的滿秩的方陣，它的單位特徵向量為 v1, v2,…, vn，對應的特徵值為 λ1, λ2,…, λn。那麼對任意向量 x=x1·v1+x2·v2+ … +xn·vn，有：

我們經過 k 次迭代：

由於 λ1, λ2,…, λn（不考慮兩個特徵值相等的情況，因為太少見了）。可知，經過 k 次迭代後。因此：

也就是說，經過 k 次迭代後，我們將得到矩陣主特徵向量的線性放縮，只要把這個向量歸一化，就得到了該矩陣的單位主特徵向量，進而可以解出矩陣的主特徵值。 

而我們在神經網路中，想求的是權重矩陣 W 的最大奇異值，根據上面幾節的推導，知道這個奇異值正是最大特徵值的開方。因此，我們可以採用 power iteration 的方式求解的單位主特徵向量，進而求出最大特徵值 λ1。論文中給出的演演算法是這樣的：

如果單純看分子，我們發現這兩步合起來就是，反覆迭代 (13) 中上下兩個式子 ，即可得到矩陣的單位主特徵向量。只不過 (13) 的每算“半”步都歸一化一次。

其實這種歸一化並不影響向量的方向收斂到主特徵向量的方向，而隻影響特徵向量前面的繫數。而每步歸一化一次的好處是，每步都可以得到單位主特徵向量的近似解。 

那麼，知道的單位主特徵向量後，如何求出最大特徵值 λ1 呢？

而將公式 (13) 的第二個式子兩邊同時左乘:

最終，(15) 即為論文中提出的權重矩陣 W 的 spectral norm 公式。 

而在具體的程式碼實現過程中，可以隨機初始化一個噪聲向量代入公式 (13) 。由於每次更新引數的 step size 很小，矩陣 W 的引數變化都很小，矩陣可以長時間維持不變。

因此，可以把引數更新的 step 和求矩陣最大奇異值的 step 融合在一起，即每更新一次權重 W ，更新一次和，並將矩陣歸一化一次（除以公式 (15) 近似算出來的 spectral norm）。 

具體程式碼見：

https://github.com/christiancosgrove/pytorch-spectral-normalization-gan