作者丨蘇劍林
單位丨廣州火焰資訊科技有限公司
研究方向丨NLP,神經網路
個人主頁丨kexue.fm
本文來給大家分享一下筆者最近的一個工作:透過簡單地修改原來的 GAN 模型,就可以讓判別器變成一個編碼器,從而讓 GAN 同時具備生成能力和編碼能力,並且幾乎不會增加訓練成本。
這個新模型被稱為 O-GAN(正交 GAN,即 Orthogonal Generative Adversarial Network),因為它是基於對判別器的正交分解操作來完成的,是對判別器自由度的最充分利用。



▲ FFHQ線性插值效果圖
背景
筆者掉進生成模型的大坑已經很久時間了,不僅寫了多篇有關生成模型的文章,而且還往 arXiv 上也提交了好幾篇跟生成模型相關的小 paper。自掉坑以來,雖然說對生成模型尤其是 GAN 的理解漸深,有時也覺得自己做出了一點改進工作(所以才提交到 arXiv上),但事實上那些東西都是無關痛癢的修修補補,意義實在不大。
而本文要介紹的這個模型,自認為比以往我做的所有 GAN 相關工作的價值總和還要大:它提供了目前最簡單的方案,來訓練一個具有編碼能力的 GAN 模型。
現如今,GAN 已經越來越成熟,越做越龐大,諸如 BigGAN [1]、StyleGAN [2] 等算是目前最先進的 GAN 模型也已被人熟知,甚至玩得不亦樂乎。不過,這幾個最先進的 GAN 模型,目前都只有生成器功能,沒有編碼器功能,也就是說可以源源不斷地生成新圖片,卻不能對已有的圖片提取特徵。
當然,帶有編碼器的 GAN 也有不少研究,甚至本人就曾做過,參考BiGAN-QP:簡單清晰的編碼 & 生成模型。但不管有沒有編碼能力,大部分 GAN 都有一個特點:訓練完成後,判別器都是沒有用的。因為理論上越訓練,判別器越退化(比如趨於一個常數)。
做過 GAN 的讀者都知道,GAN 的判別器和生成器兩個網路的複雜度是相當的(如果還有編碼器,那麼複雜度也跟它們相當),訓練完 GAN 後判別器就不要了,那實在是對判別器這個龐大網路的嚴重浪費!
一般來說,判別器的架構跟編碼器是很相似的,那麼一個很自然的想法是能不能讓判別器和編碼器共享大部分權重?
據筆者所知,過去所有的 GAN 相關的模型中,只有 IntroVAE [3] 做到了這一點。但相對而言 IntroVAE 的做法還是比較複雜的,而且目前網上還沒有成功復現 IntroVAE 的開原始碼,筆者也嘗試復現過,但也失敗了。
而本文的方案則極為簡單——透過稍微修改原來的GAN模型,就可以讓判別器轉變為一個編碼器,不管是複雜度還是計算量都幾乎沒有增加。
模型
事不宜遲,馬上來介紹這個模型。首先引入一般的 GAN 寫法:

為了不至於混淆,這裡還是不厭其煩地對符號做一些說明。其中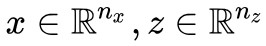 ,p(x) 是真實圖片集的“證據分佈”,q(z) 是噪聲的分佈(在本文中,它是
,p(x) 是真實圖片集的“證據分佈”,q(z) 是噪聲的分佈(在本文中,它是![]() 元標準正態分佈);而
元標準正態分佈);而 和
和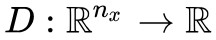 自然就是生成器和判別器了,f, g, h 則是一些確定的函式,不同的 GAN 對應著不同的 f, h, g。
自然就是生成器和判別器了,f, g, h 則是一些確定的函式,不同的 GAN 對應著不同的 f, h, g。
有時候我們會加一些標準化或者正則化手段上去,比如譜歸一化或者梯度懲罰,簡單起見,這些手段就不明顯地寫出來了。
然後定義幾個向量算符:

寫起來貌似挺高大上的,但其實就是向量各元素的均值、方差,以及標準化的向量。特別指出的是,當 nz≥3 時(真正有價值的 GAN 都滿足這個條件),[avg(z),std(z),N(z)] 是函式無關的,也就是說它相當於是原來向量 z 的一個“正交分解”。
接著,我們已經說了判別器的結構其實和編碼器有點類似,只不過編碼器輸出一個向量而判別器輸出一個標量罷了,那麼我可以把判別器寫成複合函式:

這裡 E 是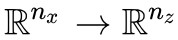 的對映,而 T 是
的對映,而 T 是 的對映。不難想象,E 的引數量會遠遠多於 T 的引數量,我們希望 E(x) 具有編碼功能。
的對映。不難想象,E 的引數量會遠遠多於 T 的引數量,我們希望 E(x) 具有編碼功能。
怎麼實現呢?只需要加一個 loss:Pearson 相關係數!

其中:
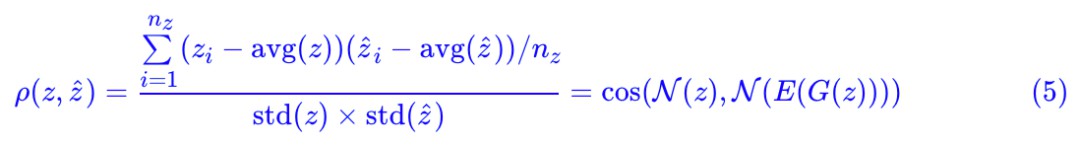
如果 λ=0,那麼就是普通的 GAN 而已(只不過判別器被分解為兩部分 E 和 T 兩部分)。加上了這個相關係數,直觀上來看,就是希望 z 和 E(G(z)) 越線性相關越好。為什麼要這樣加?我們留到最後討論。
顯然這個相關係數可以嵌入到任意現成的 GAN 中,改動量顯然也很小(拆分一下判別器、加一個 loss),筆者也做了多種 GAN 的實驗,發現都能成功訓練。
這樣一來,GAN 的判別器 D 分為了 E 和 T 兩部分,E 變成了編碼器,也就是說,判別器的大部分引數已經被利用上了。但是還剩下 T,訓練完成後 T 也是沒用的,雖然 T 的引數量比較少,這個浪費量是很少的,但對於有“潔癖”的人(比如筆者)來說還是很難受的。
能不能把 T 也省掉?經過筆者多次試驗,結論是:還真能!因為我們可以直接用 avg(E(x)) 做判別器:

這樣一來整個模型中已經沒有 T 了,只有純粹的生成器 G 和編碼器 E,整個模型沒有絲毫冗餘的地方,潔癖患者可以不糾結了。
實驗
這樣做為什麼可以?我們放到最後再說。先看看實驗效果,畢竟實驗不好的話,原理說得再漂亮也沒有意義。
註意,理論上來講,本文引入的相關係數項並不能提高生成模型的質量,所以實驗的標的主要有兩個:1)這個額外的 loss 會不會有損原來生成模型的質量;2)這個額外的 loss 是不是真的可以讓 E 變成一個有效的編碼器?
剛才也說,這個方法可以嵌入到任意 GAN 中,這次實驗用的是 GAN 是我之前的 GAN-QP 的變種:
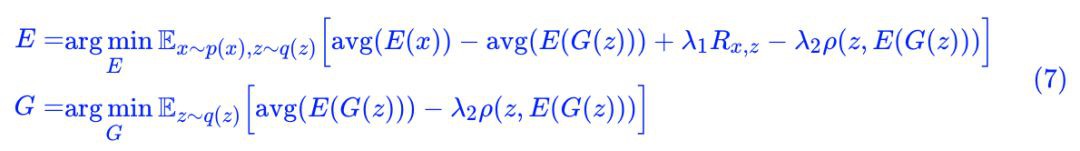
其中:

資料集上,這次的實驗做得比較完整,在 CelebA HQ、FFHQ、LSUN-churchoutdoor、LSUN-bedroom 四個資料集上都做了實驗,解析度都是 128 × 128 (其實還做了一點 256 × 256 的實驗,結果也不錯,但是沒放到論文上)。模型架構跟以往一樣都是 DCGAN [4],其餘細節直接看論文或者程式碼吧。
上圖:

▲ CelebA HQ隨機生成

▲ CelebA HQ重構效果

▲ CelebA HQ線性插值

▲ FFHQ隨機生成

▲ FFHQ重構效果

▲ FFHQ線性插值

▲ LSUN-church隨機生成

▲ LSUN-church重構效果

▲ LSUN-church線性插值

▲ LSUN-bedroom隨機生成

▲ LSUN-bedroom重構效果

▲ LSUN-bedroom線性插值
不管你們覺得好不好,反正我是覺得還好了。
1. 隨機生成效果還不錯,說明新引入的相關係數項沒有降低生成質量;
2. 重構效果還不錯,說明 E(x) 確實提取到了 x 的主要特徵;
3. 線性插值效果還不錯,說明 E(x) 確實學習到了接近線性可分的特徵。
原理
好,確認過眼神,哦不對,是效果,就可以來討論一下原理了。
很明顯,這個額外的重構項的作用就是讓 z 盡可能與 E(G(z)) “相關”,對於它,相信大多數讀者的第一想法應該是 mse 損失 而非本文用的 ρ(z,E(G(z)))。但事實上,如果加入
而非本文用的 ρ(z,E(G(z)))。但事實上,如果加入 那麼訓練基本上都會失敗。那為什麼 ρ(z,E(G(z))) 又會成功呢?
那麼訓練基本上都會失敗。那為什麼 ρ(z,E(G(z))) 又會成功呢?
根據前面的定義,E(x) 輸出一個![]() 維的向量,但是 T(E(x)) 只輸出一個標量,也就是說,E(x) 輸出了
維的向量,但是 T(E(x)) 只輸出一個標量,也就是說,E(x) 輸出了![]() 個自由度,而作為判別器,T(E(x)) 至少要佔用一個自由度(當然,理論上它也只需要佔用一個自由度)。
個自由度,而作為判別器,T(E(x)) 至少要佔用一個自由度(當然,理論上它也只需要佔用一個自由度)。
如果最小化 ,那麼訓練過程會強迫 E(G(z)) 完全等於 z,也就是說
,那麼訓練過程會強迫 E(G(z)) 完全等於 z,也就是說![]() 個自由度全部被它佔用了,沒有多餘的自由度給判別器來判別真假了,所以加入
個自由度全部被它佔用了,沒有多餘的自由度給判別器來判別真假了,所以加入 大機率都會失敗。
大機率都會失敗。
但是 ρ(z,E(G(z))) 不一樣,ρ(z,E(G(z))) 跟 avg(E(G(z))) 和 std(E(G(z))) 都沒關係(只改變向量 E(G(z)) 的 avg 和 std,不會改變 ρ(z,E(G(z))) 的值,因為 ρ 本身就先減均值除標準差了),這意味著就算我們最大化 ρ(z,E(G(z))),我們也留了至少兩個自由度給判別器。
這也是為什麼在 (6) 中我們甚至可以直接用 avg(E(x)) 做判別器,因為它不會被 ρ(z,E(G(z))) 的影響的。
一個相似的例子是 InfoGAN [5]。InfoGAN 也包含了一個重構輸入資訊的模組,這個模組也和判別器共享大部分權重(編碼器),而因為 InfoGAN 事實上只重構部分輸入資訊,因此重構項也沒佔滿編碼器的所有自由度,所以 InfoGAN 那樣做是合理的——只要給判別器留下至少一個自由度。
另外還有一個事實也能幫助我們理解。因為我們在對抗訓練的時候,噪聲是 的,當生成器訓練好之後,那麼理論上對所有的
的,當生成器訓練好之後,那麼理論上對所有的 ,G(z) 都會是一張逼真的圖片,事實上,反過來也是成立的,如果 G(z) 是一張逼真的圖片,那麼應該有
,G(z) 都會是一張逼真的圖片,事實上,反過來也是成立的,如果 G(z) 是一張逼真的圖片,那麼應該有 (即位於 N(0,Inz) 的高機率區域)。
(即位於 N(0,Inz) 的高機率區域)。
進一步推論下去,對於 ,我們有 avg(z)≈0 以及 std(z)≈1。那麼,如果 G(z) 是一張逼真的圖片,那麼必要的條件是 avg(z)≈0 以及 std(z)≈1。
,我們有 avg(z)≈0 以及 std(z)≈1。那麼,如果 G(z) 是一張逼真的圖片,那麼必要的條件是 avg(z)≈0 以及 std(z)≈1。
應用這個結論,如果我們希望重構效果好,也就是希望 G(E(x)) 是一張逼真的圖片,那麼必要的條件是 avg(E(x))≈0 以及 std(E(x))≈1。
這就說明,對於一個好的 E(x),我們可以認為 avg(E(x)) 和 std(E(x)) 都是已知的(分別等於 0 和 1),既然它們是已知的,我們就沒有必要擬合它們,換言之,在重構項中可以把它們排除掉。而事實上:
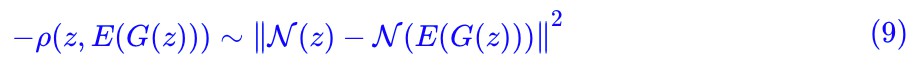
也就是說在 mse 損失中排除掉 avg(E(x)) 和 std(E(x)) 的話,然後省去常數,它其實就是 −ρ(z,E(G(z))),這再次說明瞭 ρ(z,E(G(z))) 的合理性。並且由這個推導,重構過程並不是 G(E(x)) 而是:

最後,這個額外的重構項理論上還能防止 mode collapse 的出現。其實很明顯,因為重構質量都不錯了,生成質量再差也差不到哪裡去,自然就不會怎麼 mode collapse 了。
非要說數學依據的話,我們可以將 ρ(z, E(G(z))) 理解為 Z 和 G(Z) 的互資訊上界,所以最小化 −ρ(z, E(G(z))) 事實上在最大化 Z 與 G(Z) 的互資訊,這又等價於最大化 G(Z) 的熵。而 G(Z) 的熵大了,表明它的多樣性增加了,也就遠離了 mode collapse。類似的推導可以參考能量視角下的GAN模型(二):GAN=“分析”+“取樣”。
結語
本文介紹了一個方案,只需要對原來的 GAN 進行簡單的修改,就可以將原來 GAN 的判別器轉化為一個有效的編碼器。多個實驗表明這樣的方案是可行的,而對原理的進一步思考得出,這其實就是對原始判別器(編碼器)的一種正交分解,並且對正交分解後的自由度的充分利用,所以模型也被稱為“正交 GAN(O-GAN)”。
小改動就收穫一個編碼器,何樂而不為呢?歡迎大家試用。
後記
事後看,本文模型的思想其實本質上就是“直徑和方向”的分解,並不難理解,但做到這件事情不是那麼輕鬆的。
最開始我也一直陷入到 的困境中,難以自拔,後來我想了很多技巧,終於在
的困境中,難以自拔,後來我想了很多技巧,終於在 的重構損失下也穩定住了模型(耗了幾個月),但模型變得非常醜陋(引入了三重對抗 GAN),於是我著手簡化模型。後來我嘗試用 cos 值用重構損失,發現居然能夠簡單地收斂了,於是我思考背後的原理,這可能涉及到自由度的問題。
的重構損失下也穩定住了模型(耗了幾個月),但模型變得非常醜陋(引入了三重對抗 GAN),於是我著手簡化模型。後來我嘗試用 cos 值用重構損失,發現居然能夠簡單地收斂了,於是我思考背後的原理,這可能涉及到自由度的問題。
接著我嘗試將 E(x) 分解為模長和方向向量,然後用模長 ||E(x)|| 做判別器,用 cos 做重構損失,判別器的 loss 用 hinge loss。這樣做其實幾何意義很明顯,說起來更漂亮些,部分資料集是 work 的,但是通用性不好(CelebA 還行,LSUN 不行),而且還有一個問題是 ||E(x)|| 非負,無法嵌入到一般的 GAN,很多穩定 GAN 的技巧都不能用。
然後我想怎麼把模長變成可正可負,開始想著可以對模長取對數,這樣小於 1 的模長取對數後變成負數,大於 1 的模長取對數變成正數,自然達成了目的。但是很遺憾,效果還是不好。後來陸續實驗了諸多方案都不成功,最後終於想到可以放棄模長(對應於方差)做判別器的 loss,直接用均值就行了。所以後來轉換成 avg(E(x)),這個轉變經歷了相當長的時間。
還有,重構損失一般認為要度量 x 和 G(E(x)) 的差異,而我發現只需要度量 z 和 E(G(z)) 的差異,這是最低成本的方案,因為重構是需要額外的時間的。最後,我還做過很多實驗,很多想法哪怕在 CelebA上都能成功,但LSUN上就不行。所以,最後看上去簡單的模型,實際上是艱難的沉澱。
整個模型源於我的一個執念:判別器既然具有編碼器的結構,那麼就不能被浪費掉。加上有 IntroVAE 的成功案例在先,我相信一定會有更簡單的方案實現這一點。前前後後實驗了好幾個月,跑了上百個模型,直到最近終於算是完整地解決了這個問題。
對了,除了 IntroVAE,對我啟發特別大的還有 Deep Infomax [6] 這篇論文,Deep Infomax 最後的附錄裡邊提供了一種新的做 GAN 的思路,我開始也是從那裡的方法著手思考新模型的。
參考文獻
[1] Andrew Brock, Jeff Donahue, Karen Simonyan, Large Scale GAN Training for High Fidelity Natural Image Synthesis, arXiv:1809.11096.
[2] Tero Karras, Samuli Laine, Timo Aila, A Style-Based Generator Architecture for Generative Adversarial Networks, arXiv:1812.04948.
[3] Huaibo Huang, Zhihang Li, Ran He, Zhenan Sun, Tieniu Tan, ntroVAE: Introspective Variational Autoencoders for Photographic Image Synthesis, NeurIPS 2018.
[4] Alec Radford, Luke Metz, Soumith Chintala, Unsupervised Representation Learning with Deep Convolutional Generative Adversarial Networks, ICLR 2016.
[5] Xi Chen, Yan Duan, Rein Houthooft, John Schulman, Ilya Sutskever, Pieter Abbeel, InfoGAN: Interpretable Representation Learning by Information Maximizing Generative Adversarial Nets, NIPS 2016.
[6] R Devon Hjelm, Alex Fedorov, Samuel Lavoie-Marchildon, Karan Grewal, Phil Bachman, Adam Trischler, Yoshua Bengio, Learning deep representations by mutual information estimation and maximization, ICLR 2019.
 知識星球
知識星球