作者:呱呱_
連結:https://www.jianshu.com/p/5e2d1d3cec7e
《啥是佩奇》可謂是年前的一大熱點,所謂熱點就是你在幹嘛,它都能進入你的視線。剛好有看到用Python畫佩奇的,所以就尋思著用Android也畫了一個。

佩奇完工已有些時日,一直想寫篇文章記錄下,奈何拖到現在。限於水平有限,不對的地方,還望斧正。
直接點,咱們先來看一下效果,然後再去想怎麼畫出來。

簡單分析下佩奇,會發現構圖基本由曲線構成的,還有部分使用了圓、橢圓、矩形等常規圖形。
常規圖形我們使用Canvas繪製,曲線部分我們使用Path繪製貝塞爾曲線。
所以這篇文章分為三個模組:分別介紹Canvas的使用、Path基礎、Path繪製貝塞爾曲線。
一、Canvas回顧
Canvas的使用相對基礎一點,我們來一起透過API回顧下:
| 類別 | API | 描述 |
|---|---|---|
| 繪製圖形 | drawPoint, drawPoints, drawLine, drawLines, drawRect, drawRoundRect, drawOval, drawCircle, drawArc | 依次為繪製點、直線、矩形、圓角矩形、橢圓、圓、扇形 |
| 繪製文字 | drawText, drawPosText, drawTextOnPath | 依次為繪製文字、指定每個字元位置繪製文字、根據路徑繪製文字 |
| 畫布變換 | translate, scale, rotate, skew | 依次為平移、縮放、旋轉、傾斜(錯切) |
| 畫布裁剪 | clipPath, clipRect, clipRegion | 依次為按路徑、按矩形、按區域對畫布進行裁剪 |
| 畫布狀態 | save,restore | 儲存當前畫布狀態,恢復之前儲存的畫布 |
具體到每個API就不展開說明瞭,如有需要可以檢視末尾的參考文章,都有很詳細的介紹,這裡我們畫個鼻子做示例:

圖片有些卡頓,流程還是容易知曉的:
-
繪製一個傾斜的橢圓,進度變化,閉環時上色
-
繪製兩個小圓環,進度變化,閉環時上色
-
為了繪製方便,橢圓和小圓是同時繪製的
分析完成那就開擼吧,具體數值都是yy得來的,我們主要看一下流程步驟和api的使用:
private RectF rect;
private Paint paintPink;
private Paint paintRed;
public void init() {
// 初始化矩形,各個部位的父容器,如鼻子是在矩形內部畫橢圓
rect = new RectF();
// 建立畫筆
paintPink = new Paint();
// 設定畫筆的顏色
paintPink.setColor(Color.rgb(255, 155, 192));
// 設定畫筆的填充方式:描邊
paintPink.setStyle(Paint.Style.STROKE);
// 設定畫筆的寬度
paintPink.setStrokeWidth(3f);
// 設定抗鋸齒,可以圓潤一些
paintPink.setAntiAlias(true);
...
// 其他顏色畫筆類似操作...
}
@Override
protected void onDraw(Canvas canvas) {
super.onDraw(canvas);
// 鼻子:傾斜的橢圓
rect.set(dp2px(200), dp2px(101), dp2px(250), dp2px(160));
// 旋轉畫布,結束還需旋轉回去(在這裡實現傾斜)
canvas.rotate(-15, dp2px(getContext(), 225), dp2px(getContext(), 150));
if (progressNose 100) {
// 如果進度不完整,只進行描邊操作
paintPink.setStyle(Paint.Style.STROKE);
paintRed.setStyle(Paint.Style.STROKE);
} else {
// 如果進度完整,即環形繪製完成,設定畫筆為填充樣式,設定填充及描邊(FILL_AND_STROKE)也行
paintPink.setStyle(Paint.Style.FILL);
paintRed.setStyle(Paint.Style.FILL);
}
// 畫扇形:如果角度為360度,就是矩形的內切橢圓,如果矩形為正方形,則橢圓為正圓
canvas.drawArc(rect, 0, progressNose * 3.6f, true, paintPink);
canvas.rotate(15, dp2px(getContext(), 225), dp2px(getContext(), 130));
// 鼻孔
// 重新設定矩形的引數為正方形
rect.set(dp2px(213), dp2px(125), dp2px(223), dp2px(135));
// 根據進度畫圓形鼻孔
canvas.drawArc(rect, 0, progressNose * 3.6f, false, paintRed);
rect.set(dp2px(230), dp2px(122), dp2px(240), dp2px(132));
canvas.drawArc(rect, 0, progressNose * 3.6f, false, paintRed);
}
細節註釋都有說明,至於繪製進度百分比,我們這裡使用的 ValueAnimator類。
private int progressNose = 0;
private ValueAnimator animNose;
private void initIntAnim() {
// 設定動畫的起始值,也就是我們需要的進度變化區間
animNose = ValueAnimator.ofint(0, 100);
animNose.addUpdateListener(new ValueAnimator.AnimatorUpdateListener() {
@Override
public void onAnimationUpdate(ValueAnimator animation) {
// 監聽動畫進度變化,並執行重繪操作
progressNose = (int) animation.getAnimatedValue();
invalidate();
}
});
// 設定動畫時長
animNose.setDuration(3000);
}
當只要執行這一個動畫的時候,直接呼叫 animNose.start() 就可以了。
二、Path初識
The Path class encapsulates compound (multiple contour) geometric paths consisting of straight line segments, quadratic curves, and cubic curves. It can be drawn with canvas.drawPath(path, paint), either filled or stroked (based on the paint’s Style), or it can be used for clipping or to draw text on a path.
簡單說就是:Path可以透過直線、二次、三次貝塞爾曲線,以及填充描邊樣式,做出各種炫酷效果。
Path官方檔案直通車
https://developer.android.com/reference/android/graphics/Path
我們還是來一起看一下API:
| Path 點、線操作 | 描述 |
|---|---|
| lineTo、rLineTo | 繪製線(lineTo的坐標點是相對於原點的,rLineTo的坐標點是相對於上個坐標的偏移量。) |
| moveTo、rMoveTo | 設定下一次操作的起點位置 |
| setLastPoint | 改變上一次操作結束點的位置 |
| close | 閉合Path(如果連線Path起點和終點能形成一個閉合圖形,則會將起點和終點連線起來形成一個閉合圖形。) |
| Path 常規影象 | 描述 |
|---|---|
| addRect | 繪製矩形 |
| addRoundRect | 繪製圓角矩形 |
| addCircle | 繪製圓形 |
| addOval | 繪製橢圓 |
| Path 設定方法 | 描述 |
|---|---|
| set | 將新的path賦值到已有的path |
| reset | 將path的所有操作都清空 |
| offset | 將path進行平移 |
| Path 其他屬性 | 描述 |
|---|---|
| isConvex | 判斷path是否為凸多邊形(API >= 21) |
| isEmpty | 判斷path中是否包含內容 |
| isRect | 判斷path是否是矩形 |
這裡依舊沒有展開來說,看著比較乾癟無趣,但應該會對Path的能力有所瞭解。
至於詳細使用,可以檢視精彩的參考文章:
Path從懵逼到精通(1)——基本操作
https://www.jianshu.com/p/b872b064d369
三、Path和貝塞爾曲線
3.1 我們先來假裝瞭解一下貝塞爾曲線:
以下內容摘抄自維基百科:
在數學的數值分析領域中,貝塞爾曲線(英語:Bézier curve,亦作“貝塞爾”)是計算機圖形學中相當重要的引數曲線。更高維度的廣泛化貝塞爾曲線就稱作貝茲曲面,其中貝茲三角是一種特殊的實體。
貝塞爾曲線於1962年,由法國工程師皮埃爾·貝茲(Pierre Bézier)所廣泛發表,他運用貝塞爾曲線來為汽車的主體進行設計。貝塞爾曲線最初由保爾·德·卡斯特裡奧於1959年運用德卡斯特裡奧演演算法開發,以穩定數值的方法求出貝塞爾曲線。
一階貝塞爾曲線(線性曲線)


對於一階貝賽爾曲線,我們可以理解為在起點和終點形成的這條直線上,勻速移動的點。
二階貝塞爾曲線


為建構二次貝塞爾曲線,可以中介點Q0和Q1作為由0至1的t:
-
由P0至P1的連續點Q0,描述一條線性貝塞爾曲線。
-
由P1至P2的連續點Q1,描述一條線性貝塞爾曲線。
-
由Q0至Q1的連續點B(t),描述一條二次貝塞爾曲線。
也可以說是:P0Q0 : P1Q1 = P1Q1 : P1P2 = Q0B : Q0Q1 = t
三階貝塞爾曲線
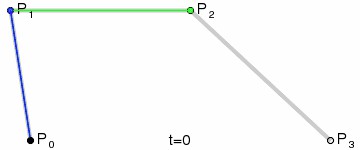
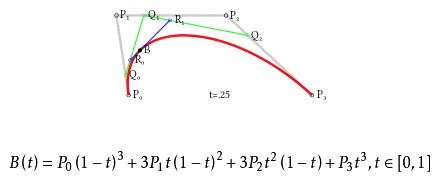
對於三次曲線,可由線性貝塞爾曲線描述的中介點Q0、Q1、Q2,和由二次曲線描述的點R0、R1所建構。
我幫大家把更更高階的貝塞爾曲線省略了…如果你覺得還想繼續深入一下,可以點選原文檢視。
3.2 Path繪製貝塞爾曲線
Android是支援貝塞爾曲線的,但是隻支援到三階,我們來一起瞭解一下:
| 類別 | API | 描述 |
|---|---|---|
| 一階 | lineTo、rLineTo | 就是繪製線 |
| 二階 | quadTo、rQuadTo | quadTo(x1, y1, x2, y2) (x1,y1) 為控制點,(x2,y2)為結束點 |
| 三階 | cubicTo、rCubicTo | cubicTo(x1, y1, x2, y2, x3, y3) (x1,y1) 為控制點,(x2,y2)為控制點,(x3,y3) 為結束點;即與二階區別多一個控制點 |
這裡我們來畫類似於口哨這麼個玩意:

這裡我們是分為兩部分進行繪製的,第一部分到拐點那裡,是個三階曲線;第二部分是個二階曲線。第一部分的終點就是第二部分的起點。
起點、終點、拐點坐標都相對好確定,可是這些控制點的坐標怎麼確定吶?
實際專案中我們可以請設計幫忙,透過ps給個大致估算,這裡只是跟著感覺試出來的,所以也就是個大致輪廓,不要介意。
程式碼比較簡單,就是坐標點的資訊有點多:
private Path mPath = new Path();
@Override
protected void onDraw(Canvas canvas) {
super.onDraw(canvas);
// 設定起始點
mPath.moveTo(dp2px(220),dp2px(102));
// 三階:頭部輪廓(畫到鼻子和嘴的連線處)
mPath.cubicTo(dp2px(-100), dp2px(80), dp2px(130), dp2px(330), dp2px(170), dp2px(170));
// 二階:畫鼻子的下麵的那條線
mPath.quadTo(dp2px(210), dp2px(170), dp2px(240), dp2px(155));
canvas.drawPath(mPath, paintPink);
}
靜態繪製這樣就完工了,可是我們怎麼才能實現動態繪製吶?
3.3 動態繪製貝塞爾曲線(TypeEvaluator估值器的使用)
為了獲取實時的坐標,我們需要透過 TypeEvaluator 打造一個屬於我們自己的估值器。
首先我們需要建立一個自己的類,用於記錄各種點資訊和具體操作資訊:
public class ViewPoint {
float x, y;
float x1, y1;
float x2, y2;
int operation;
public ViewPoint() {}
public ViewPoint(float x, float y) {
this.x = x;
this.y = y;
}
public static ViewPoint moveTo(float x, float y, int operation) {
return new ViewPoint(x, y, operation);
}
public static ViewPoint lineTo(float x, float y, int operation) {
return new ViewPoint(x, y, operation);
}
public static ViewPoint curveTo(float x, float y, float x1, float y1, float x2, float y2, int operation) {
return new ViewPoint(x, y, x1, y1, x2, y2, operation);
}
public static ViewPoint quadTo(float x, float y, float x1, float y1, int operation) {
return new ViewPoint(x, y, x1, y1, operation);
}
private ViewPoint(float x, float y, int operation) {
this.x = x;
this.y = y;
this.operation = operation;
}
public ViewPoint(float x, float y, float x1, float y1, int operation) {
this.x = x;
this.y = y;
this.x1 = x1;
this.y1 = y1;
this.operation = operation;
}
public ViewPoint(float x, float y, float x1, float y1, float x2, float y2, int operation) {
this.x = x;
this.y = y;
this.x1 = x1;
this.y1 = y1;
this.x2 = x2;
this.y2 = y2;
this.operation = operation;
}
}
再寫一個類用來記錄Path的相關操作,並且記錄到具體的ViewPoint中:
public class ViewPath {
public static final int MOVE = 0;
public static final int LINE = 1;
public static final int QUAD = 2;
public static final int CURVE = 3;
private ArrayList mPoints;
public ViewPath() {
mPoints = new ArrayList<>();
}
public void moveTo(float x, float y) {
mPoints.add(ViewPoint.moveTo(x, y, MOVE));
}
public void lineTo(float x, float y) {
mPoints.add(ViewPoint.lineTo(x, y, LINE));
}
public void curveTo(float x, float y, float x1, float y1, float x2, float y2) {
mPoints.add(ViewPoint.curveTo(x, y, x1, y1, x2, y2, CURVE));
}
public void quadTo(float x, float y, float x1, float y1) {
mPoints.add(ViewPoint.quadTo(x, y, x1, y1, QUAD));
}
public Collection getPoints() {
return mPoints;
}
}
最後就是我們的關鍵點,透過實現TypeEvaluator介面,來打造我們自己的估值器,最終傳回實時的坐標。
我們透過泛型傳入ViewPoint類,並且複寫evaluate()方法。
evaluate() 方法共有三個引數,分別是:當前進度、起始資料和終點資料。
具體計算過程則是分清每一種操作類別,然後套計算公式即可。
public class ViewPathEvaluator implements TypeEvaluator<ViewPoint> {
public ViewPathEvaluator() {}
@Override
public ViewPoint evaluate(float t, ViewPoint startValue, ViewPoint endValue) {
float x, y;
float startX, startY;
// 判斷結束點的型別,根據後一個點型別,來計算開始點和結束點的變化
if (endValue.operation == ViewPath.LINE) {
// line:畫直線,當前值 = 起始點 + t * (結束點-起始點)
// 判斷開始點的型別,找到它真正的起始點
// 如果上一步操作(startValue)是二階,取二階的結束點x1 為新起點
startX = (startValue.operation == ViewPath.QUAD) ? startValue.x1 : startValue.x;
// 如果上一步操作(startValue)是三階,取三階的結束點x2 為新起點
startX = (startValue.operation == ViewPath.CURVE) ? startValue.x2 : startX;
// 以上兩步:如果既不是二階,也不是三階,直接取startValue.x(一階)
// Y 取值方式與 X 類似
startY = (startValue.operation == ViewPath.QUAD) ? startValue.y1 : startValue.y;
startY = (startValue.operation == ViewPath.CURVE) ? startValue.y2 : startY;
x = startX + t * (endValue.x - startX);
y = startY + t * (endValue.y - startY);
} else if (endValue.operation == ViewPath.CURVE) {
// curve:三階,同上:先求真實起始點,然後套公式求值
startX = (startValue.operation == ViewPath.QUAD) ? startValue.x1 : startValue.x;
startY = (startValue.operation == ViewPath.QUAD) ? startValue.y1 : startValue.y;
startX = (startValue.operation == ViewPath.CURVE) ? startValue.x2 : startX;
startY = (startValue.operation == ViewPath.CURVE) ? startValue.y2 : startY;
float oneMinusT = 1 - t;
//三階貝塞爾函式(套公式)
x = oneMinusT * oneMinusT * oneMinusT * startX +
3 * oneMinusT * oneMinusT * t * endValue.x +
3 * oneMinusT * t * t * endValue.x1 +
t * t * t * endValue.x2;
y = oneMinusT * oneMinusT * oneMinusT * startY +
3 * oneMinusT * oneMinusT * t * endValue.y +
3 * oneMinusT * t * t * endValue.y1 +
t * t * t * endValue.y2;
} else if (endValue.operation == ViewPath.MOVE) {
// move:重新設定起點
x = endValue.x;
y = endValue.y;
} else if (endValue.operation == ViewPath.QUAD) {
startX = (startValue.operation == ViewPath.CURVE) ? startValue.x2 : startValue.x;
startY = (startValue.operation == ViewPath.CURVE) ? startValue.y2 : startValue.y;
startX = (startValue.operation == ViewPath.QUAD) ? startValue.x1 : startX;
startY = (startValue.operation == ViewPath.QUAD) ? startValue.y1 : startY;
//二階貝塞爾函式
float oneMinusT = 1 - t;
x = oneMinusT * oneMinusT * startX +
2 * oneMinusT * t * endValue.x +
t * t * endValue.x1;
y = oneMinusT * oneMinusT * startY +
2 * oneMinusT * t * endValue.y +
t * t * endValue.y1;
} else {
x = endValue.x;
y = endValue.y;
}
return new ViewPoint(x, y);
}
}
具體使用如下:
private ValueAnimator animHead;
private ViewPoint pointHead = new ViewPoint();
private Path mPath = new Path();
public void initPath() {
// 千萬不要覺得下麵很複雜,就是找貝爾塞的控制點和結束點而已,很簡單
// 我們的ViewPath,其實可以繪製任何直線路徑和貝塞爾曲線路徑了,自己在呼叫lineTo傳入點等就行了
ViewPath viewPath = new ViewPath();
pointHead.x = dp2px(220);
pointHead.y = dp2px(102);
mPath.moveTo(pointHead.x, pointHead.y);
viewPath.moveTo(pointHead.x, pointHead.y);
viewPath.curveTo(dp2px(-100), dp2px(80), dp2px(130), dp2px(330), dp2px(170), dp2px(170));
viewPath.quadTo(dp2px(210), dp2px(170), dp2px(240), dp2px(155));
animHead = ValueAnimator.ofObject(new ViewPathEvaluator(), viewPath.getPoints().toArray());
animHead.addUpdateListener(new ValueAnimator.AnimatorUpdateListener() {
@Override
public void onAnimationUpdate(ValueAnimator valueAnimator) {
// 獲取最新的坐標點,並執行重繪操作
pointHead = (ViewPoint) valueAnimator.getAnimatedValue();
invalidate();
}
}
);
animHead.setDuration(5000);
}
@Override
protected void onDraw(Canvas canvas) {
super.onDraw(canvas);
mPath.lineTo(pointHead.x, pointHead.y);
canvas.drawPath(mPath, paintPink);
}
執行下start()操作,就是一個動態繪製的豬頭了:

至於讓所有的動畫連起來繪製,則使用AnimatorSet類,playSequentially()方法是將動畫集合按順序播放。
完整程式碼請移步GitHub
https://github.com/princekin-f/Page
參考文章(連結請點選原文):
-
自定義 View——Canvas 與 ValueAnimator – Idtk
-
Path從懵逼到精通(1)——基本操作
-
Path從懵逼到精通(2)——貝塞爾曲線
-
Android 屬性動畫-繪製貝塞爾曲線路徑
-
安卓自定義View進階 – 貝塞爾曲線
-
自定義控制元件三部曲之繪圖篇(六)——Path之貝賽爾曲線和手勢軌跡、水波紋效果
-
淺析Android動畫(三),自定義Interpolator與TypeEvaluator
 知識星球
知識星球