小編邀請您,先思考:
1 相似度如何計算?
2 相似度有什麼應用?
溫馨提示:加入圈子或者商務合作,請加微信:luqin360
在資料分析和資料挖掘以及搜尋引擎中,我們經常需要知道個體間差異的大小,進而評價個體的相似性和類別。常見的比如資料分析中比如相關分析,資料挖掘中的分類聚類(K-Means等)演演算法,搜尋引擎進行物品推薦時。
相似度就是比較兩個事物的相似性。一般透過計算事物的特徵之間的距離,如果距離小,那麼相似度大;如果距離大,那麼相似度小。比如兩種水果,將從顏色,大小,維生素含量等特徵進行比較相似性。
問題定義:有兩個物件X,Y,都包含N維特徵,X=(x1,x2,x3,……..,xn),Y=(y1,y2,y3,……..,yn),計算X和Y的相似性。常用的有五種方法,如下。
1、歐幾裡得距離(Eucledian Distance)
歐氏距離是最常用的距離計算公式,衡量的是多維空間中各個點之間的絕對距離,當資料很稠密並且連續時,這是一種很好的計算方式。
因為計算是基於各維度特徵的絕對數值,所以歐氏度量需要保證各維度指標在相同的刻度級別,比如對身高(cm)和體重(kg)兩個單位不同的指標使用歐式距離可能使結果失效。

程式碼: 
2、曼哈頓距離(Manhattan Distance)
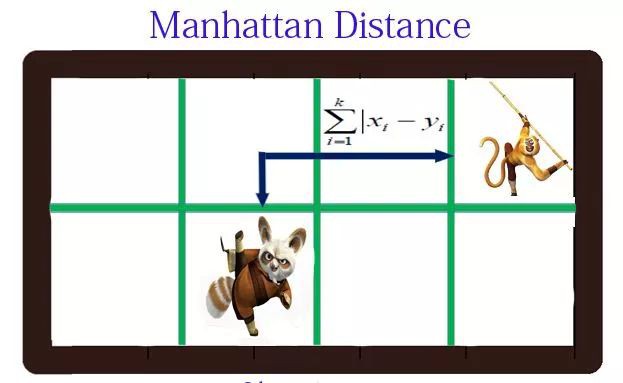
Manhattan distance = |x1 – x2| + |y1 – y2|,p1 at (x1, y1) and p2 at (x2, y2).
程式碼: 
3、明可夫斯基距離(Minkowski distance)
明氏距離是歐氏距離的推廣,是對多個距離度量公式的概括性的表述,看看下圖
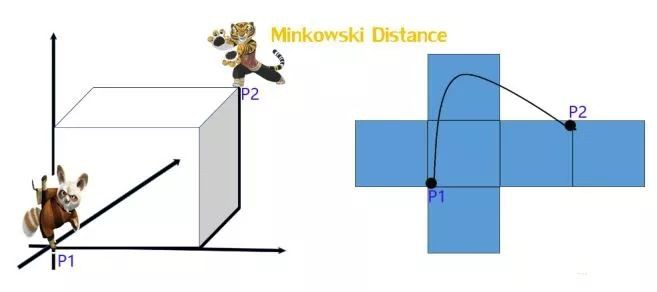
公式: 
從公式我們可以看出,
-
當p==1,“明可夫斯基距離”變成“曼哈頓距離”
-
當p==2,“明可夫斯基距離”變成“歐幾裡得距離”
-
當p==∞,“明可夫斯基距離”變成“切比雪夫距離”
程式碼: 
4、(餘弦相似度)Cosine Similarity
餘弦相似度用向量空間中兩個向量夾角的餘弦值作為衡量兩個個體間差異的大小。相比距離度量,餘弦相似度更加註重兩個向量在方向上的差異,而非距離或長度上。

程式碼: 
5、Jaccard Similarity
Jaccard繫數主要用於計算符號度量或布林值度量的個體間的相似度,因為個體的特徵屬性都是由符號度量或者布林值標識,因此無法衡量差異具 體值的大小,只能獲得“是否相同”這個結果,所以Jaccard繫數只關心個體間共同具有的特徵是否一致這個問題。

對於上面兩個物件A和B,我們用Jaccard計算它的相似性,公式如下
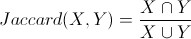
首先計算出A和B的交(A ∩ B),以及A和B的並 (A ∪ B):

然後利用公式進行計算:

程式碼:

六、皮爾森相關係數(Pearson Correlation Coefficient)
又稱相關相似性,透過Peason相關係數來度量兩個使用者的相似性。計算時,首先找到兩個使用者共同評分過的專案集,然後計算這兩個向量的相關係數。
公式:

實現彙總:

參考資料
1、Implementing the five most popular Similarity Measures in Python
2、相似度方法總結
連結:https://blog.csdn.net/yixianfeng41/article/details/61917158
親愛的讀者朋友們,您們有什麼想法,請點選【寫留言】按鈕,寫下您的留言。
資料人網(http://shujuren.org)誠邀各位資料人來平臺分享和傳播優質資料知識。
公眾號推薦:
360區塊鏈,專註於360度分享區塊鏈內容。

腳印英語,專註於分享實用口語內容。

閱讀原文,更多精彩!
分享是收穫,傳播是價值!
 知識星球
知識星球