線性判別分析（Linear Discriminant Analysis, LDA）是一種有監督降維方法，有關機器學習的書上一定少不了對 PCA 和 LDA 這兩個演演算法的介紹。LDA 的標準建模形式是這樣的（這裡以兩類版本為例，文章會在幾個關鍵點上討論多類情況）：

其中，是類間散佈矩陣，是類內散佈矩陣， w 是投影直線：

怎麼樣，一定非常熟悉吧，經典的 LDA 就是長這個樣子的。這個式子的標的也十分直觀：將兩類樣本投影到一條直線上，使得投影后的類間散佈矩陣與類內散佈矩陣的比值最大。

三個加粗的詞隱含著三個問題：

1. 為什麼是類間散佈矩陣呢？直接均值之差 m1-m2 不是更符合直覺嗎？這樣求出來的解和原來一樣嗎？ 

2. 為什麼是投影到直線，而不是投影到超平面？PCA 是把 d 維樣本投影到 c 維 (c

3. 為什麼是類間散佈與類內散佈的比值呢？差值不行嗎？ 

這篇文章就圍繞這三個問題展開。我們先回顧一下經典 LDA 的求解，然後順次講解分析這三個問題。

回顧經典LDA

原問題等價於這個形式：

然後就可以用拉格朗日乘子法了：

求導並令其為 0：

得到解：

對矩陣進行特徵值分解就可以得到 w。但是有更簡單的解法：

而其中是一個標量，所以和 λw 共線，得到：

求解完畢。非常優雅，不愧是教科書級別的經典演演算法，整個求解一氣呵成，標準的拉格朗日乘子法。但是求解中還是用到了一個小技巧：是標量，從而可以免去特徵值分解的麻煩。

那麼，我們能不能再貪心一點，找到一種連這個小技巧都不需要的求解方法呢？答案是可以，上面的問題在下一節中就能得到解決。

類間散佈 & 均值之差

我們不用類內散佈矩陣了，改用均值之差 m1-m2 這個更符合直覺的東西：

還是用拉格朗日乘子法：

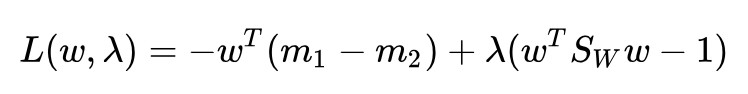
求導並令其為 0：

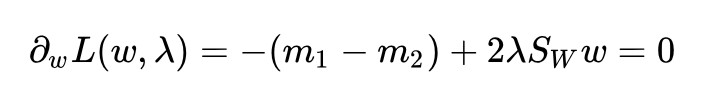
得到解：

怎麼樣，是不是求解更簡單了呢？不需要任何技巧，一步一步下來就好了。

為什麼說均值之差更符合直覺呢？大家想啊，LDA 的目的是讓投影后的兩類之間離得更遠，類內離得更近。說到類內離得更近能想到的最直接的方法就是讓類內方差最小，這正是類內散佈矩陣；說到類間離得更遠能想到的最直接的方法肯定是讓均值之差最大，而不是均值之差與自己的克羅內克積這個奇怪的東西最大。

那麼經典 LDA 為什麼會用類間散佈矩陣呢？我個人認為是這樣的運算式看起來更加優雅：分子分母是齊次的，並且這個東西恰好就是廣義瑞利商：

雖然經典 LDA 求解沒有上面這個方法直接，但是問題表述更加規範，所用到的技巧也非常簡單，不會給是使用者帶來困擾，所以 LDA 最終採用的就是類間散佈矩陣了吧。

直線 & 超平面

上面那個問題只算是小打小鬧，沒有太大的意義，但是這個問題就很有意義了：LDA 為什麼直接投影到直線（一維），而不能像 PCA 一樣投影到超平面（多維）呢？ 我們試試不就完了。 

假設將樣本投影到上，其中每一個 wi 都是經典 LDA 中的 w 。也就相當於我們不是把樣本投影到一條直線上，而是投影到 c 條直線上，也就相當於投影到了超平面上。投影后的樣本坐標為：

所以樣本的投影過程就是：

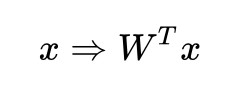
那麼，均值的投影過程也是這樣：

投影后的均值之差的二範數：

為什麼不用第一行的向量內積而偏要用第二行的跡運算呢？因為這樣可以拼湊出類間散佈來，和經典 LDA 保持形式的一致。

回顧一下經典 LDA 的形式：

現在我們有了，還缺個約束，類比一下就可以得到了：

實際上，約束也可以選擇成，這兩個約束實際上都是在限制 W 的解空間，得出來的解是等價的，這兩個約束有什麼區別呢？我只發現了一點： 

回想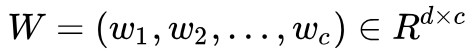是 c 條投影直線，為了確保向這 c 條直線投影能等價於向 c 維子空間投影，我們需要保證 c 條直線是線性無關的，即  rank(W) =c。看一下約束：

右邊是秩為 c 的單位矩陣，因為矩陣乘積的秩不大於每一個矩陣的秩，所以左邊這三個矩陣的秩都要不小於 c，因此我們得到了 rank(W) = c。也就是說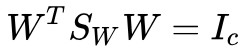，能夠保證我們在向一個 c 維子空間投影。而約束中沒有顯式地表達這一點。

我對矩陣的理解還不夠深入，不知道是否也隱含了對秩的約束，所以為了保險起見，我選擇了帶有顯式秩約束的，這樣就得到了我們的高維投影版 LDA：

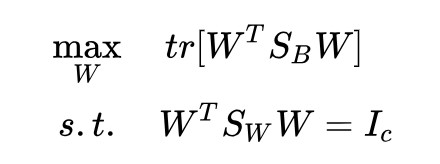
下麵來求解這個問題。還是拉格朗日乘子法：

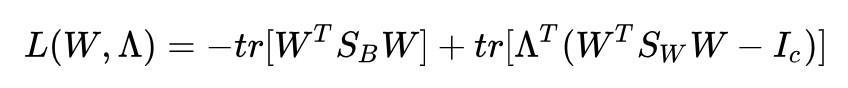
求導並令其為 0：

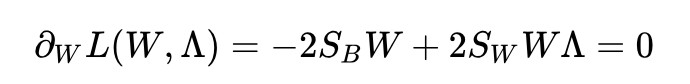
得到了：

在大部分情況下，一些協方差矩陣的和是可逆的。即使不可逆，上面這個也可以用廣義特徵值問題的方法來求解，但是這裡方便起見我們認為可逆：

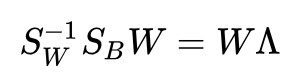
我們只要對進行特徵值分解，就可以得到 d 個特徵向量了，挑出最大特徵值對應的 c 個特徵向量來組成 W，我們不就得到向 c 維子空間的投影了嗎？

真的是這樣嗎？

不是這樣的。誠然，我們可以選出 c 個特徵向量，但是其中只有 1 個特徵向量真正是我們想要的，另外 c-1 個沒有意義。

觀察：

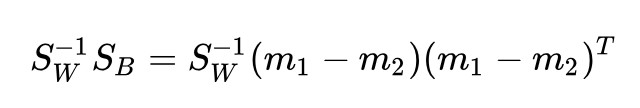
發現了嗎？等式右邊的 (m1-m2) 是一個向量，換句話說，是一個秩為 1 的矩陣。那麼，這個乘積的秩也不能大於 1，並且它不是 0 矩陣，所以：

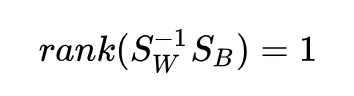
秩為 1 的矩陣只有 1 個非零特徵值，也只有 1 個非零特徵值對應的特徵向量 w。

可能有人會問了，那不是還有零特徵值對應的特徵向量嗎，用它們不行嗎？

不行。來看一下標的函式：

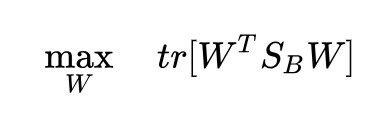
我們剛才得到的最優性條件：

所以標的函式為：

而我們的 W 只能保證 λ1, λ2, …, λd 中的一個非零，無論我們怎麼選取剩下的 c-1 個 w，標的函式也不會再增大了，因為唯一一個非零特徵值對應的特徵向量已經被選走了。 

所以，兩類 LDA 只能向一條直線投影。 

這裡順便解釋一下 K 類 LDA 為什麼只能投影到 K-1 維，其實道理是一樣的。K 類 LDA 的類間散佈矩陣是：

可以看出，是 K 個秩一矩陣的和（因為 mk-m 是秩一的向量），所以它的秩最大為 K。並且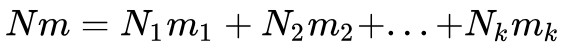，所以這 K 項中有一項可以被線性表出。所以，的秩最大為 K-1。也即：

只有 K-1 個非零特徵值。所以，K 類 LDA 最高只能投影到 K-1 維。

咦？剛才第三個問題怎麼提的來著，可不可以不用比值用差值，用差值的話會不會解決這個投影維數的限制呢？

比值 & 差值

經典 LDA 的標的函式是投影后的類間散佈與類內散佈的比值，我們很自然地就會想，為什麼非得用比值呢，差值有什麼不妥嗎？ 再試試不就完了。 

註意，這一節我們不用向量 w，而使用矩陣 W 來討論，這也就意味著我們實際上在同時討論二類 LDA 和多類 LDA，只要把和換成對應的就好了。

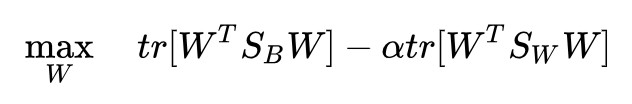
註意到可以透過放縮 W 來得到任意大的標的函式，所以我們要對 W 的規模進行限制，同時也進行秩限制：

也就得到了差值版的 LDA：

依然拉格朗日乘子法：

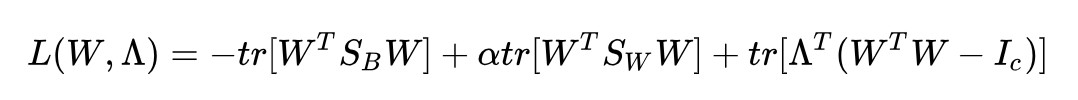
求導並令其為 0：

得到了：

由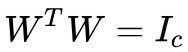，有：

可以得到：

若括號內的東西可逆，則上式可以寫為：

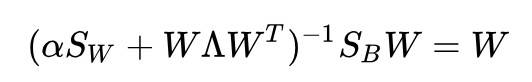
註意到， 的秩不大於 K-1，說明等號左邊的秩不大於 K-1，那麼等號右邊的秩也不大於 K-1，即：

所以我們還是會遇到秩不足，無法求出 K-1 個以上的非零特徵值和對應的特徵向量。這樣還不夠，我們還需要證明的一點是，新的標的函式在零特徵值對應的特徵向量下依然不會增加。

標的函式（稍加變形）為：

再利用剛才我們得到的最優性條件（稍加變形）：

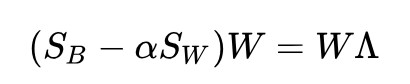
所以標的函式為：

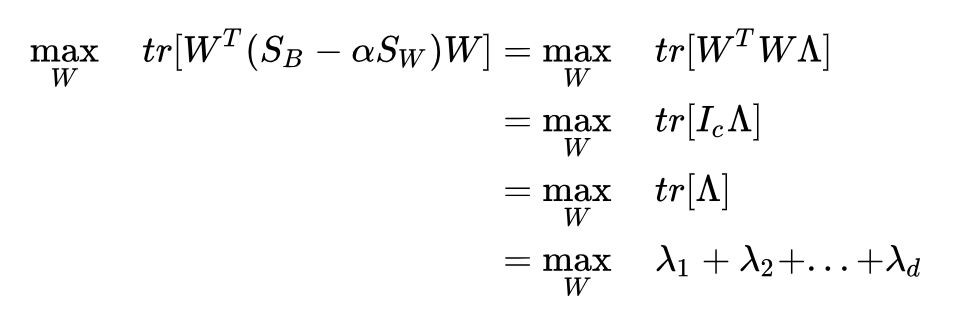
結論沒有變化，新的標的函式依然無法在零特徵值的特徵向量下增大。 

綜合新矩陣依然秩不足和零特徵值依然對新標的函式無貢獻這兩點，我們可以得到一個結論：用差值代替比值也是可以求解的，但是我們不會因此受益。 

既然比值和差值算出來的解性質都一樣，那麼為什麼經典 LDA 採用的是比值而不是差值呢？ 

我個人認為，這可能是因為比值算出來的解還有別的直覺解釋，而差值的可能沒有，所以顯得更優雅一些。什麼直覺解釋呢？ 

在二分類問題下，經典 LDA 是最小平方誤差準則的一個特例。若讓第一類的樣本的輸出值等於 N/N1 ，第二類樣本的輸出值等於 -N/N2 ， N 代表相應類樣本的數量，然後用最小平方誤差準則求解這個模型，得到的解恰好是（用比值的）LDA 的解。這個部分 PRML 上有講解。

總結

這篇文章針對教科書上 LDA 的標的函式丟擲了三個問題，並做了相應解答，在這個過程中一步一步深入理解 LDA。

第一個問題：可不可以用均值之差而不是類間散佈？

答案：可以，這樣做更符合直覺，並且更容易求解。但是採用類間散佈的話可以把 LDA 的標的函式表達成廣義瑞利商，並且上下齊次更加合理。可能是因為這些原因，經典 LDA 最終選擇了類間散佈。

第二個問題：可不可以把 K 類 LDA 投影到大於 K-1 維的子空間中？

答案：不可以，因為類間散佈矩陣的秩不足。K 類 LDA 只能找到 K-1 個使標的函式增大的特徵值對應的特徵向量，即使選擇了其他特徵向量，我們也無法因此受益。

第三個問題：可不可以用類間散佈與類內散佈的差值，而不是比值？

答案：可以，在新準則下可以得到新的最優解，但是我們無法因此受益，K 類 LDA 還是隻能投影到 K-1 維空間中。差值版 LDA 與比值版 LDA 相比還缺少了一個直覺解釋，可能是因為這些原因，經典 LDA 最終選擇了比值。

所以，教科書版 LDA 如此經典是有原因的，它在各個方面符合了人們的直覺，本文針對它提出的三個問題都沒有充分的理由駁倒它，經典果然是經典。