推薦 ：一文讀懂最大似然估計(附R程式碼)

簡介

解釋模型如何工作是資料科學中最為基本最為關鍵的問題之一。當你建立了一個模型之後，它給了你預期的結果，但是它背後的過程是什麼呢？作為一個資料科學家，你需要對這個經常被問到的問題做出解答。

例如，假設您建立了一個預測公司股價的模型。您註意到夜深人靜的時候，股票價格上漲得很快。背後可能有多種原因，找出可能性最大的原因便是最大似然估計的意義所在。這一概念常被用於經濟學、MRIs、衛星成像等領域。

來源：YouTube 

在這篇文章中，我們將研究最大似然估計(以下簡稱MLE)是如何工作的，以及它如何用於確定具有任何分佈的模型的繫數。理解MLE將涉及到機率和數學，但我將嘗試透過例子使它更通俗易懂。

註：如前所述，本文假設您已經瞭解機率論的基本知識。您可以透過閱讀這篇文章來澄清一些基本概念：

《每個資料科學專業人員都應該知道的機率分佈常識》：

https://www.analyticsvidhya.com/blog/2017/09/6-probability-distributions-data-science/

目錄

• 為什麼要使用最大似然估計(MLE)？

• 透過一個實體瞭解MLE

• 進一步瞭解技術細節

• 分佈引數

• 似然

• 對數似然

• 最大似然估計

• 利用MLE確定模型繫數

• R語言的MLE實現

為什麼要使用最大似然估計(MLE)？

假設我們想預測活動門票的銷售情況。資料的直方圖和密度如下。

你將如何為這個變數建模？該變數不是正態分佈的，而且是不對稱的，因此不符合線性回歸的假設。一種常用的方法是對變數進行對數、平方根（sqrt）、倒數等轉換，使轉換後的變數服從正態分佈，併進行線性回歸建模。

讓我們試試這些轉換，看看結果如何：

• 對數轉換：

• 平方根轉換：
  

• 倒數轉換：
  

所有這些都不接近正態分佈，那麼我們應該如何對這些資料進行建模，才能不違背模型的基本假設？如何利用正態分佈以外的其他分佈來建模這些資料呢？如果我們使用了不同的分佈，又將如何來估計繫數？

這便是最大似然估計(MLE)的主要優勢。

舉一個例子來加深對MLE的理解

在研究統計和機率時，你肯定遇到過諸如x＞100的機率，因為x服從正態分佈，平均值為50，標準差為10。在這些問題中，我們已經知道分佈（在這種情況下是正態分佈）及其引數（均值和標準差），但在實際生活問題中，這些引數是未知的，並且必須從資料中估計出來。MLE可以幫助我們確定給定資料的分佈引數。

讓我們用一個例子來加深理解：假設我們用資料來表示班級中學生的體重(以kg為單位)。資料如下圖所示(還提供了用於生成資料圖的R程式碼)：

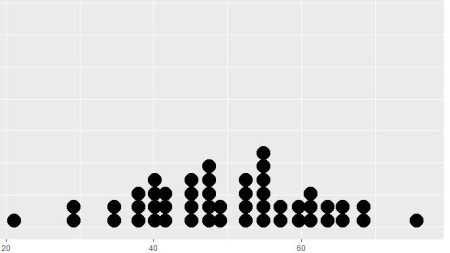
圖 1 

x = as.data.frame(rnorm(50,50,10))

ggplot(x, aes(x = x)) + geom_dotplot()

這似乎遵循正態分佈。但是我們如何得到這個分佈的均值和標準差呢？一種方法是直接計算給定資料的平均值和標準差，分別為49.8公斤和11.37公斤。這些值能很好地表示給定的資料，但還不能最好地描述總體情況。

我們可以使用MLE來獲得更穩健的引數估計。因此，MLE可以定義為從樣本資料中估計總體引數(如均值和方差、泊松率(Lambda)等)的方法，從而使獲得觀測資料的機率(可能性)最大化。

為了加深對MLE的理解，嘗試猜測下列哪一項會使觀察上述資料的機率最大化？

1. 均值=100，標準差=10

2. 均值=50 ，標準差=10

顯然，如果均值為100，我們就不太可能觀察到上述資料分佈圖形。

進一步瞭解技術細節

知道MLE能做什麼之後，我們就可以深入瞭解什麼是真正的似然估計，以及如何對它最大化。首先，我們從快速回顧分佈引數開始。

• 分佈引數

首先，來瞭解一下分佈引數。維基百科對這個詞的定義如下：“它是一個機率分佈的量化指數”，可以將它視為樣本總數的數值特徵或一個統計模型。透過下麵的圖表來理解它：

圖 2

鐘形曲線的寬度和高度的兩個引數決定均值和方差。這就是正態分佈的分佈引數。同樣，泊松分佈由一個引數lambda控制，即事件在時間或空間間隔內發生的次數。

圖 3

大多數分佈都有一個或兩個引數，但有些分佈可以有多達4個引數，比如4引數β分佈。

• 似然

從圖2和圖3中我們可以看到，給定一組分佈引數，一些資料值比其他資料的機率更大。從圖1中，我們已經看到，當平均值是50而不是100時，給定的資料更有可能發生。然而，在現實中，我們已經觀察到了這些資料。因此，我們面臨著一個逆向問題：給定觀測資料和一個感興趣的模型，我們需要在所有機率密度中找到一個最有可能產生資料的機率密度函式/機率質量函式(f(x_\θ)。

為解決這一逆向問題，我們透過逆轉f(x=θ)中資料向量x和(分佈)引數向量θ來定義似然函式，即：

L(θ;x) = f(x| θ)

在MLE中，可以假定我們有一個似然函式L(θ；x)，其中θ是分佈引數向量，x是觀測集。我們感興趣的是尋找具有給定觀測值(x值)的最大可能性的θ值。

• 對數似然

如果假設觀測集(Xi)是獨立的同分佈隨機變數，機率分佈為f0(其中f0=正態分佈，例如圖1)，那麼手頭的數學問題就變得簡單了。似然函式可以簡化為：

為了求這個函式的極大值/極小值，我們可以取此函式w.r.tθ的導數，並將其設為0(因為零斜率表示最大值或極小值)。因為我們這裡有乘積，所以需要應用鏈式規則，這對乘積來說是相當麻煩的。一個聰明的訣竅是取似然函式的對數，並使其最大化。這將乘積轉換為加法，並且由於對數是一個嚴格遞增的函式，因此不會影響θ的結果值。所以我們有：

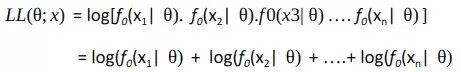
• 最大化似然

為找到對數似然函式LL（Th；x）的極大值，我們可以：

• 取LL(θ；x)函式w.r.tθ的一階導數，並將其等價於0；

• 取LL(θ；x)函式w.r.tθ的二階導數，並確認其為負值。

在許多情況下，微積分對最大化似然估計沒有直接幫助，但最大值仍然可以很容易地識別出來。在尋找最大對數似然值的引數值時，沒有任何東西比一階導數等於零具有更為 “優先”或特殊的位置。當需要估計一些引數時，它僅僅是一個方便的工具而已。

在通常情況下，能對函式求最大值的argmax的方法都可能適合於尋找log似然函式的最大值。這是一個無約束的非線性最佳化問題。我們尋求一種最佳化演演算法以下列方式工作：

• 從任意起始點可靠地收斂到區域性最小化

• 速度盡可能快

使用最佳化技術來最大化似然是非常常見的，可以有多種方法來實現(比如：牛頓法、Fisher評分法、各種基於共軛梯度的方法、最陡下降法、Nder-Mead型(單純形)方法、BFGS法和多種其他技術)。

結果表明，當模型假設為高斯時，MLE估計等價於一般的最小二乘法。

你可以參考下麵這篇文章來證明它：

link：

http://people.math.gatech.edu/~ecroot/3225/maximum_likelihood.pdf

用MLE確定模型繫數

現在讓我們看看如何使用MLE來確定預測模型的繫數。

假設我們有一個n個觀測量y1，y2，…，yn的樣本，它們可以被看作是獨立的泊松隨機變數：Yi ∼ P(µi)。此外，假設我們希望讓均值i(方差也同樣！)依賴於變數xi組成的向量。我們可以構成如下簡單的線性模型：

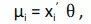
中θ是模型繫數的向量。這個模型的缺點是右邊的線性預測器可以假定為任何實際值，而表示期望計數的左側泊松均值必須是非負的。這個問題的一個簡單的解決辦法是用線性模型來模擬平均值的對數。因此，我們考慮了一個具有對數連結對數的廣義線性模型，它可以寫成如下所示：

我們的目的是利用MLE找到θ。

現在，泊松分佈如下：

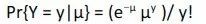
利用在上一節中學到的對數似然概念來求θ。取上述方程的對數，忽略包含log(y！)的常數，我們得到的對數似然函式是：

其中，µi依賴協變數xi和θ繫數的向量。我們可以用變元µi = exp(xi’θ)代替，求解方程，得到最大似然值θ。得到了θ向量之後，我們就可以透過乘以xi和θ向量來預測平均值的期望值。

用R語言實現MLE

在本節中，我們將採用一個真實的資料集，運用前面學到的概念，來解決一個問題。您可以從此連結下載資料集：

https://s3-ap-south-1.amazonaws.com/av-blog-media/wp-content/uploads/2018/07/ Train_Tickets.csv

資料集中的示例如下：

             售票日期           計票     

25-08-2012 00:00      8

25-08-2012 01:00      2

25-08-2012 02:00      6

25-08-2012 03:00      2

25-08-2012 04:00      2

25-08-2012 05:00      2

它有從2012年8月25日到2014年9月25日每小時售出的門票數量(約18K記錄)。我們的目的是預測每小時售出的門票數量。這是本文第一節中討論的同一個資料集。

這個問題可以用回歸、時間序列等技術來解決。在這裡，我們將使用我們已經學習到的統計建模技術，用R語言實現。

首先，分析一下資料。在統計建模中，我們更關心的是標的變數是如何分佈的。讓我們看一看計數的分佈：

hist(Y$Count, breaks = 50,probability = T ,main = “Histogram of Count Variable”)

lines(density(Y$Count), col=”red”, lwd=2)

這可以看作是泊松分佈，或者我們甚至可以嘗試擬合指數分佈。

由於手頭的變數是票的計數，泊松分佈是一個更合適的模型。指數分佈通常用於模擬事件之間的時間間隔。

讓我們來計算一下這兩年售出的票的數量：

看上去隨著時間的推移，門票的銷售有了很大的增長。為了將問題簡單化，讓我們僅將時間作為一個因子來建模，其中時間定義為2012年8月25日以來幾個星期。我們可以把它寫成：

其中，µ（售出的票數）是泊松分佈的平均值，而θ0和θ1是我們需要估計的繫數。

組合方程1和2，我們得到如下的對數似然函式：

我們可以使用Rstats 4包中的mle() 函式來估計繫數θ0和θ1。它需要下列主要引數：

• 需要最小化的負似然函式：這與我們剛剛匯出的函式相同，但前面有一個負號[最大對數似然度等於最小化負對數似然]。

• 繫數向量的起點：這是繫數的初始預測值。結果可以根據這些值而變化，因為函式可能達到區域性最小值。因此，透過執行不同起點的函式來驗證結果是很好的辦法。

• BFGS是預設的對似然函式進行最佳化的方法。

在我們的示例中，負對數似然函式的編碼如下：

nll

    x

    y

    mu = exp(theta0 + x*theta1)

    -sum(y*(log(mu)) – mu)

}

我將資料分為訓練集和測試集，以便客觀地評價模型的效能。idx是測試集中行的指數。

set.seed(200)

idx

接下來，呼叫mle函式來獲得引數：

est

summary(est)

 

Maximum likelihood estimation

Call:

stats4::mle(minuslogl = nll, start = list(theta0 = 2, theta1 = 0))

 

Coefficients:

         Estimate  Std. Error

theta0 2.68280754 2.548367e-03

theta1 0.03264451 2.998218e-05

 

-2 log L: -16594396

我們得到了繫數的估計值，利用RMSE作為獲得測試集結果的評估度量：

pred.ts

rmse(pred.ts, Y$Count[idx])

 

86.95227

現在，讓我們看看我們的模型和標準線性模型(正態分佈的誤差)的對比，本模型是用對數計數建模。

lm.fit

 

Coefficients:

             Estimate Std. Error t value Pr(>|t|)    

(Intercept) 1.9112992 0.0110972   172.2 <2e-16 ***

age         0.0414107 0.0001768   234.3 <2e-16 ***

pred.lm

rmse(exp(pred.lm), Y$Count[idx]) 

 

93.77393

可以看出來，標準線性模型的RMSE比我們的泊松分佈模型要高。讓我們比較這兩個模型在樣本上的殘差圖，看看這些模型在不同的區域中表現如何：

與常規線性回歸相比，泊松回歸的誤差更接近於零。

在Python中，也可以透過使用scipy.optimize.minimize()函式來實現標的函式的最小化，對初始值的估計同BFGS、L-BFGS等引數和方法類似。

在R語言中，使用stats包中的glm 函式建模更加簡單。它支援泊松，伽瑪，二項分佈，Quasi，逆高斯，擬二項分佈，擬泊松分佈等等。對於上面所示的示例，可以使用以下命令直接獲得繫數：

glm(Count ~ age, family = “poisson”, data = Y)

 

Coefficients:

             Estimate Std. Error z value Pr(>|z|)    

(Intercept) 2.669     2.218e-03    1203 <2e-16 ***

age         0.03278   2.612e-05    1255 <2e-16 ***

在Python中也可以使用pymc.glm()函式，並設定為pm.glm.Familes.Poisson()系列。

尾註

對上述例子的一種思考是，引數空間中是否存在比標準線性模型估計更好的繫數。正態分佈是預設分佈，也是最廣泛使用的分佈形式，但如果採用其它更為正確的分佈，則可以得到更好的結果。最大似然估計是一種可以用於估計分佈引數而不考慮所使用的分佈的技術。因此，下次當您手頭有建模問題時，首先看看資料的分佈情況，看看有沒有比正態分佈更有意義的分佈！

詳細的程式碼和資料在我的Gizub儲存庫中可以找到。

有關使用年齡變數的資料讀取、格式化和建模的示例，請參閱“ModelingSingleVariables.R”檔案。此外，我還使用了多個變數進行建模，它儲存於“ModelingMultipleVariables.R”檔案中。

原文標題：

An Introductory Guide to Maximum Likelihood Estimation (with a case study in R)

原文連結：

https://www.analyticsvidhya.com/blog/2018/07/introductory-guide-maximum-likelihood-estimation-case-study-r/

譯者簡介：陳之炎，北京交通大學通訊與控制工程專業畢業，獲得工學碩士學位，歷任長城計算機軟體與系統公司工程師，大唐微電子公司工程師，現任北京吾譯超群科技有限公司技術支援。目前從事智慧化翻譯教學系統的運營和維護，在人工智慧深度學習和自然語言處理（NLP）方面積累有一定的經驗。

轉自：資料派THU 公眾號；

關聯閱讀：