(點選上方公眾號,可快速關註)
轉自:hjimce
blog.csdn.net/hjimce/article/details/50810129
一、字典學習
字典學習也可簡單稱之為稀疏編碼,字典學習偏向於學習字典D。從矩陣分解角度,看字典學習過程:給定樣本資料集Y,Y的每一串列示一個樣本;字典學習的標的是把Y矩陣分解成D、X矩陣:
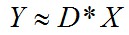
同時滿足約束條件:X盡可能稀疏,同時D的每一列是一個歸一化向量。
D稱之為字典,D的每一列稱之為原子;X稱之為編碼向量、特徵、繫數矩陣;字典學習可以有三種標的函式形式
(1)第一種形式:
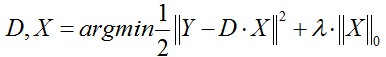
這種形式因為L0難以求解,所以很多時候用L1正則項替代近似。
(2)第二種形式:

ε是重構誤差所允許的最大值。
(3)第三種形式:
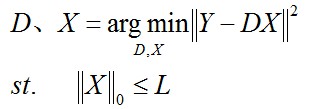
L是一個常數,稀疏度約束引數,上面三種形式相互等價。
因為標的函式中存在兩個未知變數D、X,K-svd是字典學習的一種經典演演算法,其求解方法跟lasso差不多,固定其中一個,然後更新另外一個變數,交替迭代更新。
如果D的列數少於Y的行數,就相當於欠完備字典,類似於PCA降維;如果D的列數大於Y的行數,稱之為超完備字典;如果剛好等於,那麼就稱之為完備字典。
二、k-svd字典學習演演算法概述
給定訓練資料Y,Y的每一串列示一個樣本,我們的標的是求解字典D的每一列(原子)。
K-svd演演算法,個人感覺跟k-means差不多,是k-means的一種擴充套件,字典D的每一列就相當於k-means的聚類中心。
其實球面k-means也是一種特殊的稀疏編碼(具體可參考文獻《Learning Feature Representations with K-means》),只不過k-means的編碼矩陣X是一個高度稀疏的矩陣,X的每一列就只有一個非零的元素,對應於該樣本所歸屬的聚類中心;而稀疏編碼X的每一列允許有幾個非零元素。
1、隨機初始化字典D(類似k-means一樣初始化)
從樣本集Y中隨機挑選k個樣本,作為D的原子;並且初始化編碼矩陣X為0矩陣。
2、固定字典,求取每個樣本的稀疏編碼
編碼過程採用如下公式:
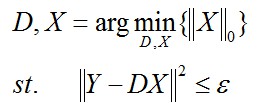
ε是重構誤差所允許的最大值。
假設我們的單個樣本是向量y,為了簡單起見我們就假設原子只有這4個,也就是字典D=[α1、α2、α3、α4],且D是已經知道的;我們的標的是計算y的編碼x,使得x儘量的稀疏。
(1)首先從α1、α2、α3、α4中找出與向量y最近的那個向量,也就是分別計算點乘:
α1*y、α2*y、α3*y、α4*y
然後求取最大值對應的原子α。
(2)假設α2*y最大,那麼我們就用α2,作為我們的第一個原子,然後我們的初次編碼向量就為:
x1=(0,b,0,0)
b是一個未知引數。
(3)求解繫數b:
y-b*α2=0
方程只有一個未知引數b,是一個高度超靜定方程,求解最小二乘問題。
(4)然後我們用x1與α2相乘重構出資料,然後計算殘差向量:
y’=y-b*α2
如果殘差向量y’滿足重構誤差閾值範圍ε,那麼就結束,否則就進入下一步;
(5)計算剩餘的字典α1、α3、α4與殘差向量y’的最近的向量,也就是計算
α1*y’、α3*y’、α4*y’
然後求取最大值對應的向量α,假設α3*y’為最大值,那麼就令新的編碼向量為:
x2=(0,b,c,0)
b、c是未知引數。
(6)求解繫數b、c,於是我們可以列出方程:
y-b*α2-c*α3=0
方程中有兩個未知引數b、c,我們可以進行求解最小二乘方程,求得b、c。
(7)更新殘差向量y’:
y’=y-b*α2-c*α3
如果y’的模長滿足閾值範圍,那麼就結束,否則就繼續迴圈,就這樣一直迴圈下去。
3、逐列更新字典、並更新對應的非零編碼
透過上面那一步,我們已經知道樣本的編碼。接著我們的標的是更新字典、同時還要更新編碼。
K-svd採用逐列更新的方法更新字典,就是當更新第k列原子的時候,其它的原子固定不變。假設我們當前要更新第k個原子αk,令編碼矩陣X對應的第k行為xk,則標的函式為:

上面的方程,我們需要註意的是xk不是把X一整行都拿出來更新(因為xk中有的是零、有的是非零元素,如果全部抽取出來,那麼後面計算的時候xk就不再保持以前的稀疏性了),所以我們只能抽取出非零的元素形成新的非零向量,然後Ek只保留xk對應的非零元素項。
上面的方程,我們可能可以透過求解最小二乘的方法,求解αk,不過這樣有存在一個問題,我們求解的αk不是一個單位向量,因此我們需要採用svd分解,才能得到單位向量αk。
進過svd分解後,我們以最大奇異值所對應的正交單位向量,作為新的αk,同時我們還需要把繫數編碼xk中的非零元素也給更新了(根據svd分解)。
然後演演算法就在1和2之間一直迭代更新,直到收斂。
def dict_update(phi, matrix_y, matrix_sparse, k):
indexes = np.where(matrix_sparse[k, :] != 0)[0]#取出稀疏編碼中,第k行不為0的列的索引
phi_temp = phi
sparse_temp = matrix_sparse
if len(indexes) > 0:
phi_temp[:, k][:] = 0#把即將更新的字典的第k列先給設定為0
matrix_e_k = matrix_y[:, indexes] – phi_temp.dot(sparse_temp[:, indexes])#取出樣本資料中,字典第k列有貢獻的值,並求Ek
u, s, v = svds(np.atleast_2d(matrix_e_k), 1)
phi_temp[:, k] = u[:, 0]
sparse_temp[k, indexes] = np.asarray(v)[0] * s[0]
return phi_temp, sparse_temp
參考文獻:
1、《Learning Feature Representations with K-means》
2、Restauration parcimonieuse d’unsignal multidimensionnel :algorithme K-SVD
覺得本文有幫助?請分享給更多人
關註「演演算法愛好者」,修煉程式設計內功
 知識星球
知識星球