(點選上方公眾號,可快速關註)
轉自:chenbjin
https://www.cnblogs.com/chenbjin/p/4200790.html
主成分分析(PCA)是一種基於變數協方差矩陣對資料進行壓縮降維、去噪的有效方法,PCA的思想是將n維特徵對映到k維上(k
1、協方差 Covariance
變數X和變數Y的協方差公式如下,協方差是描述不同變數之間的相關關係,協方差>0時說明 X和 Y是正相關關係,協方差<0時 X和Y是負相關關係,協方差為0時 X和Y相互獨立。
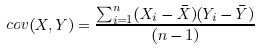
協方差的計算是針對兩維的,對於n維的資料集,可以計算C(n,2)種協方差。 n維資料的協方差矩陣的定義如下:

Dim(x)表示第x維。
對於三維(x,y,z),其協方差矩陣如下,可看出協方差矩陣是一個對稱矩陣(symmetrical),其對角線元素為每一維的方差:

2、特徵向量和特徵值
可以這樣理解:矩陣A作用在它的特徵向量X上,僅僅使得X的長度發生了變化,縮放比例就是相應的特徵值。
特徵向量只能在方陣中找到,而且並不是所有的方陣都有特徵向量,並且如果一個n*n的方陣有特徵向量,那麼就有n個特徵向量。一個矩陣的所有特徵向量是正交的,即特徵向量之間的點積為0,一般情況下,會將特徵向量歸一化,即向量長度為1。
3、PCA過程
第一步,獲取資料,下圖中的Data為原始資料,一共有兩個維度,可看出二維平面上的點。

下圖是Data在二維坐標平面上的散點圖:

第二步,減去平均值,對於Data中的每一維資料分別求平均值,並減去平均值,得到DataAdjust資料。
第三步,計算DataAdjust的協方差矩陣
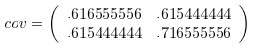
第四步,計算協方差矩陣的特徵向量和特徵值,選取特徵向量


特徵值0.490833989對應的特徵向量是(-0.735178656, 0.677873399),這裡的特徵向量是正交的、歸一化的,即長度為1。
下圖展示DataAdjust資料和特徵向量的關係:
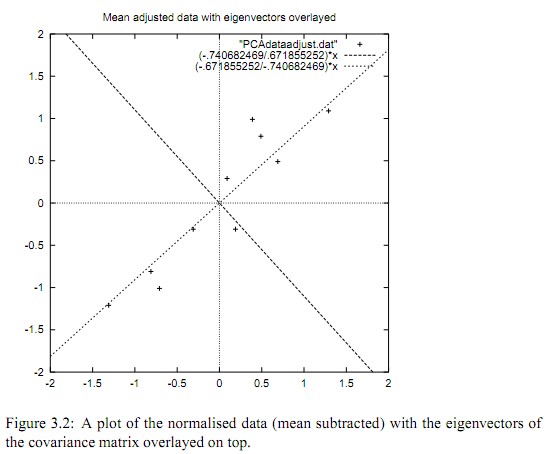
正號表示預處理後的樣本點,斜著的兩條線就分別是正交的特徵向量(由於協方差矩陣是對稱的,因此其特徵向量正交),特徵值較大的那個特徵向量是這個資料集的主要成分(principle component)。
通常來說,當從協方差矩陣計算出特徵向量之後,下一步就是透過特徵值,對特徵向量進行從大到小的排序,這將給出成分意義的順序。成分的特徵值越小,其包含的資訊量也就越少,因此可以適當選擇。
如果資料中有n維,計算出n個特徵向量和特徵值,選擇前k個特徵向量,然後最終的資料集合只有k維,取的特徵向量命名為FeatureVector。

這裡特徵值只有兩個,我們選擇其中最大的那個,1.28402771,對應的特徵向量是![]() 。
。
第五步,將樣本點投影到選取的特徵向量上,得到新的資料集
假設樣例數為m,特徵數為n,減去均值後的樣本矩陣為DataAdjust(m*n),協方差矩陣是n*n,選取的k個特徵向量組成的矩陣為EigenVectors(n*k)。那麼投影后的資料FinalData為
![]()
這裡是FinalData(10*1) = DataAdjust(10*2矩陣)×特徵向量![]()
得到結果為

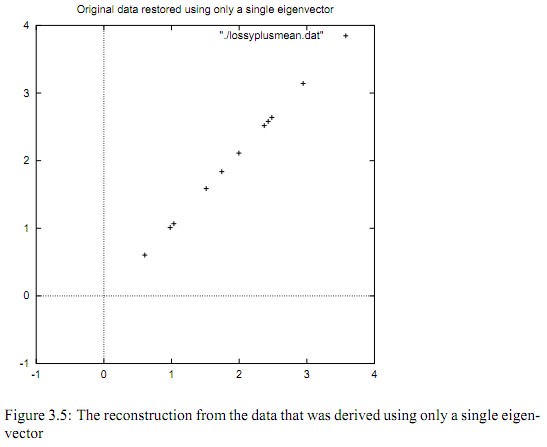
下圖是FinalData根據最大特徵值對應的特徵向量轉化回去後的資料集形式,可看出是將DataAdjust樣本點分別往特徵向量對應的軸上做投影:
如果取的k=2,那麼結果是
![clip_image014[4]](http://pic.ipshop.xyz/wx/JUdS9hOHejh.jpg)
可見,若使用了所有特徵向量得到的新的資料集,轉化回去之後,與原來的資料集完全一樣(只是坐標軸旋轉)。
覺得本文有幫助?請分享給更多人
關註「演演算法愛好者」,修煉程式設計內功
 知識星球
知識星球