導讀:
線性代數往往是學習機器學習和深度學習的一大障礙,為瞭解決這個問題,我們特別邀請了 Udacity 機器學習&深度學習導師 Aaron,幫助大家梳理神經網路中涉及的數學知識,以及理解其物理含義。希望大家讀過之後,可以使大家對於神經網路有更多角度的理解,幫助大家推導以及理解其中的數學公式。
線性代數
矩陣乘以向量的物理含義
矩陣乘法我更喜歡稱作線性轉換。一個矩陣乘以向量中,矩陣相當於一個轉換函式,而向量是一個輸入,已知了輸入和函式,我們就可以知道輸出。這裡需要強調的是,向量共有兩種形式,一種為列向量,一種為行向量。在預設情況下,向量是指列向量。大部分的國內教材中,並沒有特意提到這一點。很多人接觸到編寫程式碼時,都是以行向量的形式開始學習,導致後續有很多概念產生混淆。在本文中,若無特殊說明,向量的形式預設為列向量。
首先我們先看以下的2道熱身題:
1. 假設讀者並不知道矩陣乘法的運算準則,能否在假想的幾何空間中,快速地反應出答案是多少呢?給大家30s。(記住,不可以透過運演演算法則來進行計算)
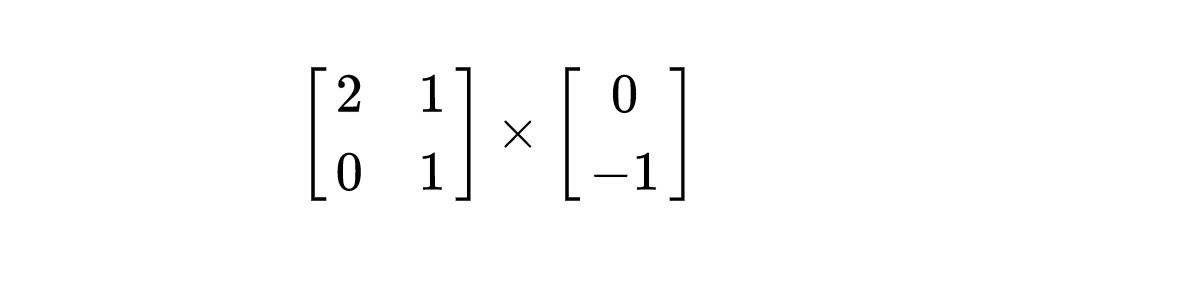
2. 同樣地,利用假想的幾何空間想象,是否可以立即解答出矩陣M是什麼?
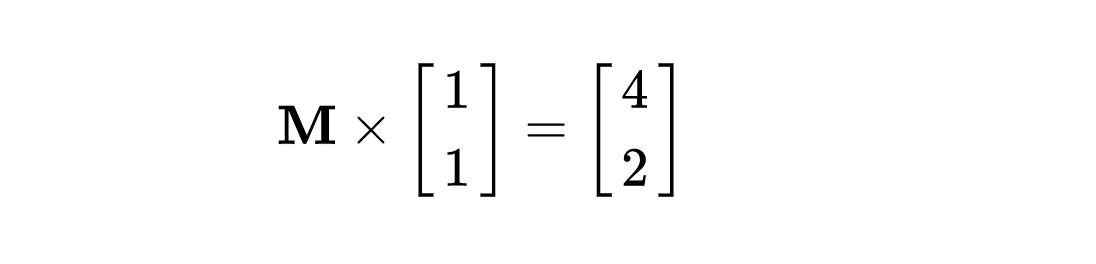
如果讀者可以快速解答出上面的問題,那麼恭喜您,您已經瞭解了線性代數空間轉換的本質;如果沒有解答出,那就是我寫這篇文章的意義。
先拋開上面兩道題,這裡來介紹一下矩陣。
線性代數與空間幾何是存在緊密的聯絡的。基本所有的線性代數都有其對應的幾何表示方法。理解幾何,是理解線性代數的核心所在。
以二維空間來說,舉個慄子:

現在,我們來看一張動圖:

更多動圖的資訊請關註3Blue1Brown主頁,裡面有大量衝破你數學世界觀的知識。3Blue1Brown還有影片集。B站有做了很贊的漢化,不過更鼓勵大家去看英文原版影片。

我們來繼續看看錶示方法:

這其中的區別就是基向量不一樣了,而線性組合的繫數 -1 與 2 保持固定不變。
我們把變換後的基向量放在一起,變為矩陣:

我們在來看另一幅動圖來實踐一下,找到這幅動圖的線性變換矩陣是什麼?

根據上面的方法,鎖定綠色與紅色基向量末尾的位置,這幅動圖的線性變換矩陣為

而其原來所有坐標繫上的向量都隨之變換髮生改變。
現在再回頭看看上面的兩道題?是否能夠透過想象的空間去快速找到答案?

如果不是方陣咋辦?
上面我們講的是方陣,那麼如果不是方陣呢?比如一個 3 x 2 的矩陣,或者一個 2 x 3 的矩陣呢? (以下我們只用中括號來代表具體矩陣的形狀,具體數字並不重要。)
我們來以 3 x 2 矩陣形式舉例,如下所示:

3 x 2 的矩陣的物理含義就是把一個向量從二維表示方法轉換到三維表示。而轉換矩陣的每一列就代表:將二維空間對應的基向量轉換到三維的樣子。將這種變換規律對映到其他變換的二維向量;同樣地, 2 x 3 矩陣物理含義就是將一個向量從三維表示轉換成二維表示。轉換矩陣每一列代表:三維空間的基向量對映到二維空間之後的樣子。將這種變換規律對映到其他變換的三維向量。
現在,我們再進行下一步操作。如果我們假設讓一個4維向量,先轉化為3維向量,在轉化為二維向量,那麼它的形式是什麼樣子的呢?

透過以上形式,我們可以發現如果將一個列向量經過多次線性轉換,他的順序應該是從右至左的順序。這就是標準的線性代數書中所講到的連續線性變換的形式,從右至左也是線性代數數學家習慣的順序。
但是,在很多神經網路包括深度學習網路的課程中我們可以看到,更符合我們閱讀的順序是將一個輸入資料拿進來之後經過一次矩陣轉換,從左至右得到輸出結果。他們之間有什麼聯絡呢?
透過觀察我們可以知道,這其中最大的原因在於資料的形式,也就是上文中提到的每一個樣本表示方法是列向量還是行向量。如果是列向量,變換的順序就是從右至左;如果是行向量,變換順序就是從左至右。而相應的矩陣形狀也發生反轉。

-
所有形式為矩陣乘以矩陣
神經網路中,大家都希望最終的形式為矩陣乘以矩陣,不希望中間有任何向量的存在,這樣顯得更酷,實際上計算也更快。這很簡單,現在我們只差最後一步。當我們把所有資料放在一起,還是如上方有 m 個 4 維行向量形式的資料,我們將這些行向量資料堆疊在一起形成 m x 4的矩陣,經過多個矩陣的變換之後輸出為一個 m x 2 的矩陣。這樣,在計算過程中,全部為不同形狀的矩陣。當然,大家也可以想想如果是列向量該是什麼形式。
以上內容想說明的就是,無論是上方哪一種形式,都是正確的。關鍵看輸入的資料是什麼形式,形式決定了資料變換的順序,以及設計矩陣的形狀。
透過以上的形式,其實神經網路前向傳導和向量在不同維度間的連續線性變換及其相似。唯一不同的一點就在於,在每次線性轉換後,神經網路可以加一個非線性啟用函式,使線性轉換變為非線性轉換。實際上,也就這麼點區別。而非線性啟用函式並不會改變資料的形狀,對後續矩陣乘法不造成任何影響。
小結一下上麵線性代數部分我們發現了什麼:
-
線性代數中的向量預設形式是列向量。
-
矩陣的實質就是將坐標整體線性變換。
-
矩陣的組合以列向量組合在一起,其代表各自的基向量變換之後的新向量是什麼。
-
矩陣與向量相乘,矩陣與矩陣相乘,順序很重要,其決定權在於實際問題中樣本的表達形式,是行向量還是列向量。
-
神經網路的前向傳導與線性代數中連續對於向量的線性變換過程極其相似,只是在層與層之間多了非線性啟用函式。
神經網路求的是什麼?其實就是上方這麼多矩陣中每一個位置的數字是多少?這就是我們最終的目的。那麼如何求?這就需要微積分中鏈式法則的知識了。

囿於篇幅限制,微積分中鏈式法則的知識部分,
請感興趣的同學掃碼入群,獲取完整文章,免費閱讀
?
這部分作者會用儘量少的公式,記住極少的關鍵點,幫助大家去順利的推導神經網路中運用到的鏈式推導。
總結
希望經過上述自己的梳理,大家對於神經網路中涉及到的數學知識有了更進一步形象化的瞭解。
點選[閱讀原文],給自己一個成為矽谷認證機器學習工程師的機會!
 知識星球
知識星球


