(點選上方公眾號,可快速關註)
轉自:BYRans
http://www.cnblogs.com/BYRans/p/4700202.html
牛頓方法(Newton’s method)
邏輯回歸中利用Sigmoid函式g(z)和梯度上升來最大化ℓ(θ)。現在我們討論另一個最大化ℓ(θ)的演演算法—-牛頓方法。
牛頓方法是使用迭代的方法尋找使f(θ)=0的θ值,在這裡θ是一個真實的值,不是一個引數,只不過θ的真正取值不確定。牛頓方法數學運算式為:

牛頓方法簡單的理解方式為:先隨機選一個點,然後求出f在該點的切線,即f在該點的導數。該切線等於0的點,即該切線與x軸相交的點為下一次迭代的值。直至逼近f等於0的點。過程如下圖:
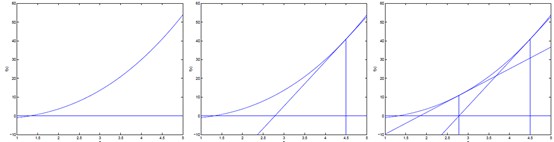
牛頓方法最大化Likelihood
牛頓方法提供了一種尋找f(θ)=0的θ值的方法。怎麼用於最大化似然函式ℓ (θ)呢?ℓ的最大值對應點處的一階導數ℓ'(θ)為零。
所以讓f(θ) = ℓ'(θ),最大化ℓ (θ)就可以轉化為:用牛頓方法求ℓ'(θ)=0的θ的問題。由牛頓方法的運算式,θ的迭代更新公式為:

牛頓-拉夫森迭代法(Newton-Raphson method)
邏輯回歸中θ是一個向量,所以我們把上面的運算式推廣到多維的情況就是牛頓-拉夫森迭代法(Newton-Raphson method),運算式如下:
![]()
運算式中 表示的ℓ(θ)對
表示的ℓ(θ)對 的偏導數;H是一個n*n的矩陣,稱為Hessian矩陣。Hessian矩陣的運算式為:
的偏導數;H是一個n*n的矩陣,稱為Hessian矩陣。Hessian矩陣的運算式為:

牛頓方法VS梯度下降
如下圖是一個最小化一個標的方程的例子,紅色曲線是利用牛頓法迭代求解,綠色曲線是利用梯度下降法求解:

牛頓方法通常比梯度下降收斂速度快,迭代次數也少。
但因為要計算Hessian矩陣的逆,所以每次迭代計算量比較大。當Hessian矩陣不是很大時牛頓方法要優於梯度下降。
覺得本文有幫助?請分享給更多人
關註「演演算法愛好者」,修煉程式設計內功
 知識星球
知識星球