演演算法科普：神秘的 DES 加密演演算法

1、前言

DES 演演算法是一種常見的分組加密演演算法，由IBM公司在1971年提出。DES 演演算法是分組加密演演算法的典型代表，同時也是應用最為廣泛的對稱加密演演算法。本文將詳細講述DES 的原理以及實現過程。

1.1 明文

明文是指沒有經過加密的資料。一般而言，明文都是等待傳輸的資料。由於沒有經過加密，明文很容易被識別與破解，因此在傳輸明文之前必須進行加密處理。

1.2 密文

密文只是明文經過某種加密演演算法而得到的資料，通常密文的形式複雜難以識別及理解。

1.3 金鑰

金鑰是一種引數，它是在明文轉換為密文或將密文轉換為明文的演演算法中輸入的引數。

1.4 對稱加密

通訊雙方同時掌握一個金鑰，加密解密都是由一個金鑰完成的（即加密金鑰等於解密金鑰，加解密金鑰可以相互推倒出來）。雙方通訊前共同擬定一個金鑰，不對第三方公開。

1.5 分組密碼

分組密碼是將明文分成固定長度的組，每一組都採用同一金鑰和演演算法進行加密，輸出也是固定長度的密文。

2、DES 加密演演算法

2.1 分組長度

DES 加密演演算法中，明文和密文為 64 位分組。金鑰的長度為 64 位，但是金鑰的每個第八位設定為奇偶校驗位，因此金鑰的實際長度為56位。

2.2 加密流程

DES 加密演演算法大致分為 4 個步驟：

（1）初始置換
（2）生成子金鑰
（3）迭代過程
（4）逆置換

整個過程流程圖：

加密流程

3、初始置換

初始置換是將原始明文經過IP置換表處理。置換過程如圖：

例如：
輸入64位明文資料M（64位）：
明文M（64位）=
0110001101101111011011010111000001110101011101000110010101110010
選取金鑰K（64位）：
金鑰K（64位）=
0001001100110100010101110111100110011011101111001101111111110001

IP置換表：

58,50,42,34,26,18,10,02,
60,52,44,36,28,20,12,04,
62,54,46,38,30,22,14,06,
64,56,48,40,32,24,16,08,
57,49,41,33,25,17,09,01,
59,51,43,35,27,19,11,03,
61,53,45,37,29,21,13,05,
63,55,47,39,31,23,15,07,

IP置換表中的資料指的是位置，例如58指將M第58位放置第1位。

M經過IP置換後為M’

M’（64位） =
1111111110111000011101100101011100000000111111110000011010000011
取M’的前32位作為L0，則有
L0（32位）= 11111111101110000111011001010111
取M’的後32位作為R0，則有
R0（32位）= 00000000111111110000011010000011

4、生成子金鑰

DES 加密共執行16次迭代，每次迭代過程的資料長度為48位，因此需要16個48位的子金鑰來進行加密，生成子金鑰的過程如下：

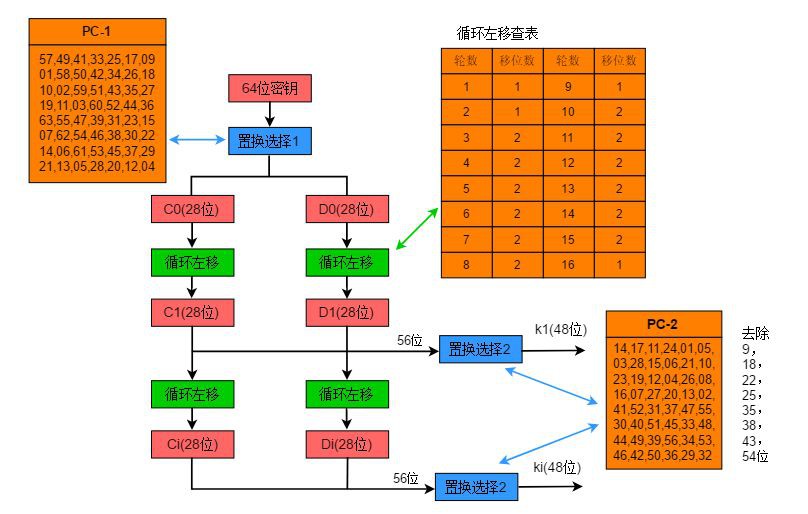
以第3節的例子說明子金鑰的計算過程：

（1）第一輪置換：

金鑰 K = 0001001100110100010101110111100110011011101111001101111111110001需經過PC-1表置換，即執行置換選擇1過程。
PC-1表為：

57,49,41,33,25,17,09
01,58,50,42,34,26,18
10,02,59,51,43,35,27
19,11,03,60,52,44,36
63,55,47,39,31,23,15
07,62,54,46,38,30,22
14,06,61,53,45,37,29
21,13,05,28,20,12,04

PC-1表為8行7列的表，金鑰K經PC-1後變為56位資料K’。

K’（56位）= 11110000110011001010101011110101010101100110011110001111
取K’的前28位作為C0，則有
C0（28位）= 1111000011001100101010101111
取K’的後28位作為D0，則有
D0（28位）= 0101010101100110011110001111
獲得C0，D0後進行左移操作需要查詢移動位數表：

每輪移動移動位數表如下：

輪數 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
位數 1 1 2 2 2 2 2 2 1  2   2   2   2  2   2   1

進行第一輪移位，輪數為1，查表得左移位數為1。

C0左移1位為C1：
C1（28位） = 1110000110011001010101011111
D0左移1位為D1：
D1（28位） = 1010101011001100111100011110
將C1和D1合併後，經過PC-2表置換得到子金鑰K1，PC-2表中去除了第9，18，22，25，35，38，43，54位。

PPC-2表為6X8的表，PC-2表如下：

14,17,11,24,01,05,
03,28,15,06,21,10,
23,19,12,04,26,08,
16,07,27,20,13,02,
41,52,31,37,47,55,
30,40,51,45,33,48,
44,49,39,56,34,53,
46,42,50,36,29,32

由於PC-2表為6X8的表，經PC-2置換後的資料為48位，置換後得到金鑰K1，
K1（48位）= 000110110000001011101111111111000111000001110010

（2）第二輪置換

C1和D1再次左移，輪數 = 2，查表得左移位數 = 1，則C1和D1左移1位得到C2和D2。

C2（28位）= 1100001100110010101010111111
D2（28位）= 0101010110011001111000111101
C2和D2合併後為56位，經過PC-2表置換得到金鑰K2（48位）
K2（48位）= 011110011010111011011001110110111100100111100101
依次類推，得到K3-K16子金鑰，註意Ci和Di左移的位數。

C3（28位） = 0000110011001010101011111111
D3（28位） = 0101011001100111100011110101
K3（48位） = 010101011111110010001010010000101100111110011001

C4（28位） = 0011001100101010101111111100
D4（28位） = 0101100110011110001111010101
K4（48位） = 011100101010110111010110110110110011010100011101

C5（28位） = 1100110010101010111111110000
D5（28位） = 0110011001111000111101010101
K5（48位） = 011111001110110000000111111010110101001110101000

C6（28位） = 0011001010101011111111000011
D6（28位） = 1001100111100011110101010101
K6（48位） = 011000111010010100111110010100000111101100101111

C7（28位） = 1100101010101111111100001100
D7（28位） = 0110011110001111010101010110
K7（48位） = 111011001000010010110111111101100001100010111100

C8（28位） = 0010101010111111110000110011
D8（28位） = 1001111000111101010101011001
K8（48位） = 111101111000101000111010110000010011101111111011

C9（28位） = 0101010101111111100001100110
D9（28位） = 0011110001111010101010110011
K9（48位） = 111000001101101111101011111011011110011110000001

C10（28位） = 0101010111111110000110011001
D10（28位） = 1111000111101010101011001100
K10（48位） = 101100011111001101000111101110100100011001001111

C11（28位） = 0101011111111000011001100101
D11（28位） = 1100011110101010101100110011
K11（48位） = 001000010101111111010011110111101101001110000110

C12（28位） = 0101111111100001100110010101
D12（28位） = 0001111010101010110011001111
K12（48位） = 011101010111000111110101100101000110011111101001

C13（28位） = 0111111110000110011001010101
D13（28位） = 0111101010101011001100111100
K13（48位） = 100101111100010111010001111110101011101001000001

C14（28位） = 1111111000011001100101010101
D14（28位） = 1110101010101100110011110001
K14（48位） = 010111110100001110110111111100101110011100111010

C15（28位） = 1111100001100110010101010111
D15（28位） = 1010101010110011001111000111
K15（48位） = 101111111001000110001101001111010011111100001010

C16（28位） = 1111000011001100101010101111
D16（28位） = 0101010101100110011110001111
K16（48位） = 110010110011110110001011000011100001011111110101

5、迭代過程

設Li（32位）和Ri（32位）為第i次迭代結果的左半部分與右半部分，子金鑰Ki為第i輪的48位加密金鑰。定義運算規則：

Li = Ri-1;
Ri = Li ⊕ f(Ri-1, Ki);

整個迭代過程如下圖：

5.1 擴充套件置換E

右半部分Ri的位數為32位，而金鑰長度Ki為48位，為了能夠保證Ri與Ki可以進行異或運算需要對Ri位數進行擴充套件，用於擴充套件置換表E如下：

擴充套件置換表E：

32,01,02,03,04,05,
04,05,06,07,08,09,
08,09,10,11,12,13,
12,13,14,15,16,17,
16,17,18,19,20,21,
20,21,22,23,24,25,
24,25,26,27,28,29,
28,29,30,31,32,01

例如：
L0（32位） = 11111111101110000111011001010111
R0（32位） = 00000000111111110000011010000011
R0（32位）經過擴充套件置換後變為48位資料：
E(R0)（48位） = 100000000001011111111110100000001101010000000110

將E(R0)（48位）與K1（48位）作異或運算

100000000001011111111110100000001101010000000110
000110110000001011101111111111000111000001110010
= 100110110001010100010001011111001010010001110100

得到：
E(R0)^K1（48位） = 100110110001010100010001011111001010010001110100

5.2 S-盒替代

代替運算由8個不同的代替盒（S盒）完成。每個S盒有6位輸入，4位輸出。代替運算流程如下：

S-盒1：

14,04,13,01,02,15,11,08,03,10,06,12,05,09,00,07,
00,15,07,04,14,02,13,01,10,06,12,11,09,05,03,08,
04,01,14,08,13,06,02,11,15,12,09,07,03,10,05,00,
15,12,08,02,04,09,01,07,05,11,03,14,10,00,06,13,

S-盒2：

15,01,08,14,06,11,03,04,09,07,02,13,12,00,05,10,
03,13,04,07,15,02,08,14,12,00,01,10,06,09,11,05,
00,14,07,11,10,04,13,01,05,08,12,06,09,03,02,15,
13,08,10,01,03,15,04,02,11,06,07,12,00,05,14,09,

S-盒3：

10,00,09,14,06,03,15,05,01,13,12,07,11,04,02,08,
13,07,00,09,03,04,06,10,02,08,05,14,12,11,15,01,
13,06,04,09,08,15,03,00,11,01,02,12,05,10,14,07,
01,10,13,00,06,09,08,07,04,15,14,03,11,05,02,12,

S-盒4：

07,13,14,03,00,06,09,10,01,02,08,05,11,12,04,15,
13,08,11,05,06,15,00,03,04,07,02,12,01,10,14,09,
10,06,09,00,12,11,07,13,15,01,03,14,05,02,08,04,
03,15,00,06,10,01,13,08,09,04,05,11,12,07,02,14,

S-盒5：

02,12,04,01,07,10,11,06,08,05,03,15,13,00,14,09,
14,11,02,12,04,07,13,01,05,00,15,10,03,09,08,06,
04,02,01,11,10,13,07,08,15,09,12,05,06,03,00,14,
11,08,12,07,01,14,02,13,06,15,00,09,10,04,05,03,

S-盒6：

12,01,10,15,09,02,06,08,00,13,03,04,14,07,05,11,
10,15,04,02,07,12,09,05,06,01,13,14,00,11,03,08,
09,14,15,05,02,08,12,03,07,00,04,10,01,13,11,06,
04,03,02,12,09,05,15,10,11,14,01,07,06,00,08,13,

S-盒7：

04,11,02,14,15,00,08,13,03,12,09,07,05,10,06,01,
13,00,11,07,04,09,01,10,14,03,05,12,02,15,08,06,
01,04,11,13,12,03,07,14,10,15,06,08,00,05,09,02,
06,11,13,08,01,04,10,07,09,05,00,15,14,02,03,12,

S-盒8：

13,02,08,04,06,15,11,01,10,09,03,14,05,00,12,07,
01,15,13,08,10,03,07,04,12,05,06,11,00,14,09,02,
07,11,04,01,09,12,14,02,00,06,10,13,15,03,05,08,
02,01,14,07,04,10,08,13,15,12,09,00,03,05,06,11,

S盒的計算規則：
例如：若S-盒1的輸入為110111，第一位與最後一位構成11，十進位制值為3，則對應第3行，中間4位為1011對應的十進位制值為11，則對應第11列。查詢S-盒1表的值為14，則S-盒1的輸出為1110。8個S盒將輸入的48位資料輸出為32位資料。

按照S-盒的計算過程，將
E(R0)^K1（48位）= 100110110001010100010001011111001010010001110100，透過 S- 盒替換得到的S盒輸出為10001011110001000110001011101010（32位）。

5.3 P-盒置換

將S-盒替代的輸出結果作為P-盒置換的輸入。P-盒置換表如下：

16,07,20,21,29,12,28,17,01,15,23,26,05,18,31,10,
02,08,24,14,32,27,03,09,19,13,30,06,22,11,04,25,

將S盒輸出10001011110001000110001011101010（32位）經過P盒置換，P-盒置換輸出01001000101111110101010110000001

令擴充套件置換E、S-盒替代、P盒置換的過程作為函式f。

第一次迭代過程f(R0,K1)為：
f(R0,K1) = 01001000101111110101010110000001

計算L1（32位）= R0 = 00000000111111110000011010000011
計算R1（32位）= L0 ^ f(R0,K1)
11111111101110000111011001010111
01001000101111110101010110000001
= 10110111000001110010001111010110

R1（32位） = 10110111000001110010001111010110。
將L1與R1作為輸入，繼續執行迭代過程f。直至輸出L16與R16。

經過16次迭代後輸出:

L16（32位）= 00110000100001001101101100101000
R16（32位）= 10110001011001010011000000011000

6、逆置換

將初始置換進行16次的迭代，即進行16層的加密變換，得到L16和R16，將此作為輸入塊，進行逆置換得到最終的密文輸出塊。逆置換是初始置換的逆運算。從初始置換規則中可以看到，原始資料的第1位置換到了第40位，第2位置換到了第8位。則逆置換就是將第40位置換到第1位，第8位置換到第2位。以此類推，逆置換規則表如下

40,08,48,16,56,24,64,32,
39,07,47,15,55,23,63,31,
38,06,46,14,54,22,62,30,
37,05,45,13,53,21,61,29,
36,04,44,12,52,20,60,28,
35,03,43,11,51,19,59,27,
34,02,42,10,50,18,58 26,
33,01,41,09,49,17,57,25,

逆置換過程圖：

將L16與R16構成64位資料，經過逆置換表輸出密文為：

密文：0101100000001000001100000000101111001101110101100001100001101000

7、結語

DES 加密演演算法為最為常見的分組加密演演算法。其主要思想在於資料位的置換與移位過程，透過16次的迭代加密與最終的逆置換得出最終的密文。DES 的解密方式只需按照加密的逆過程求解即可。由於DES 加密過程的演演算法是公開的，所以金鑰K的保密就顯得尤為重要，只有傳送方與接收方採用相同的金鑰進行加密解密才能獲取明文資料。