
作者丨蘇劍林
單位丨廣州火焰資訊科技有限公司
研究方向丨NLP,神經網路
個人主頁丨kexue.fm
筆者去年曾寫過文章《果殼中的條件隨機場(CRF In A Nutshell)》[1],以一種比較粗糙的方式介紹了一下條件隨機場(CRF)模型。然而那篇文章顯然有很多不足的地方,比如介紹不夠清晰,也不夠完整,還沒有實現,在這裡我們重提這個模型,將相關內容補充完成。
本文是對 CRF 基本原理的一個簡明的介紹。當然,“簡明”是相對而言中,要想真的弄清楚 CRF,免不了要提及一些公式,如果只關心呼叫的讀者,可以直接移到文末。
圖示
按照之前的思路,我們依舊來對比一下普通的逐幀 softmax 和 CRF 的異同。
逐幀softmax
CRF 主要用於序列標註問題,可以簡單理解為是給序列中的每一幀都進行分類,既然是分類,很自然想到將這個序列用 CNN 或者 RNN 進行編碼後,接一個全連線層用 softmax 啟用,如下圖所示:

▲ 逐幀softmax並沒有直接考慮輸出的背景關係關聯
條件隨機場
然而,當我們設計標簽時,比如用 s、b、m、e 的 4 個標簽來做字標註法的分詞,標的輸出序列本身會帶有一些背景關係關聯,比如 s 後面就不能接 m 和 e,等等。逐標簽 softmax 並沒有考慮這種輸出層面的背景關係關聯,所以它意味著把這些關聯放到了編碼層面,希望模型能自己學到這些內容,但有時候會“強模型所難”。
而 CRF 則更直接一點,它將輸出層面的關聯分離了出來,這使得模型在學習上更為“從容”:

▲ CRF在輸出端顯式地考慮了背景關係關聯
數學
當然,如果僅僅是引入輸出的關聯,還不僅僅是 CRF 的全部,CRF 的真正精巧的地方,是它以路徑為單位,考慮的是路徑的機率。
模型概要
假如一個輸入有 n 幀,每一幀的標簽有 k 中可能性,那麼理論上就有k^n中不同的輸入。我們可以將它用如下的網路圖進行簡單的視覺化。在下圖中,每個點代表一個標簽的可能性,點之間的連線表示標簽之間的關聯,而每一種標註結果,都對應著圖上的一條完整的路徑。

▲ 4tag分詞模型中輸出網路圖
而在序列標註任務中,我們的正確答案是一般是唯一的。比如“今天天氣不錯”,如果對應的分詞結果是“今天/天氣/不/錯”,那麼標的輸出序列就是 bebess,除此之外別的路徑都不符合要求。
換言之,在序列標註任務中,我們的研究的基本單位應該是路徑,我們要做的事情,是從 k^n 條路徑選出正確的一條,那就意味著,如果將它視為一個分類問題,那麼將是 k^n 類中選一類的分類問題。
這就是逐幀 softmax 和 CRF 的根本不同了:前者將序列標註看成是 n 個 k 分類問題,後者將序列標註看成是 1 個 k^n 分類問題。
具體來講,在 CRF 的序列標註問題中,我們要計算的是條件機率:

為了得到這個機率的估計,CRF 做了兩個假設:
假設一:該分佈是指數族分佈。
這個假設意味著存在函式 f(y1,…,yn;x),使得:

其中 Z(x) 是歸一化因子,因為這個是條件分佈,所以歸一化因子跟 x 有關。這個 f 函式可以視為一個打分函式,打分函式取指數並歸一化後就得到機率分佈。
假設二:輸出之間的關聯僅發生在相鄰位置,並且關聯是指數加性的。
這個假設意味著 f(y1,…,yn;x) 可以更進一步簡化為:

這也就是說,現在我們只需要對每一個標簽和每一個相鄰標簽對分別打分,然後將所有打分結果求和得到總分。
線性鏈CRF
儘管已經做了大量簡化,但一般來說,(3) 式所表示的機率模型還是過於複雜,難以求解。於是考慮到當前深度學習模型中,RNN 或者層疊 CNN 等模型已經能夠比較充分捕捉各個 y 與輸出 x 的聯絡,因此,我們不妨考慮函式 g 跟 x 無關,那麼:
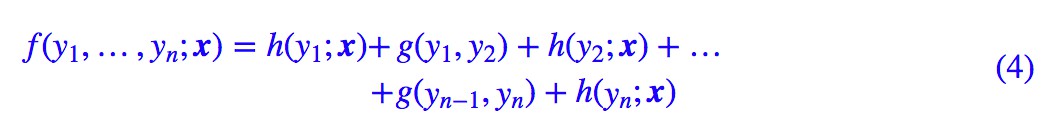
這時候 g 實際上就是一個有限的、待訓練的引數矩陣而已,而單標簽的打分函式 h(yi;x) 我們可以透過 RNN 或者 CNN 來建模。因此,該模型是可以建立的,其中機率分佈變為:

這就是線性鏈 CRF 的概念。
歸一化因子
為了訓練 CRF 模型,我們用最大似然方法,也就是用:

作為損失函式,可以算出它等於:

其中第一項是原來機率式的分子的對數,它標的的序列的打分,雖然它看上去挺迂迴的,但是並不難計算。真正的難度在於分母的對數 logZ(x) 這一項。
歸一化因子,在物理上也叫配分函式,在這裡它需要我們對所有可能的路徑的打分進行指數求和,而我們前面已經說到,這樣的路徑數是指數量級的(k^n),因此直接來算幾乎是不可能的。
事實上,歸一化因子難算,幾乎是所有機率圖模型的公共難題。幸運的是,在 CRF 模型中,由於我們只考慮了臨近標簽的聯絡(馬爾可夫假設),因此我們可以遞迴地算出歸一化因子,這使得原來是指數級的計算量降低為線性級別。
具體來說,我們將計算到時刻 t 的歸一化因子記為 Zt,並將它分為 k 個部分:

其中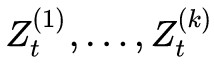 分別是截止到當前時刻 t 中、以標簽 1,…,k 為終點的所有路徑的得分指數和。那麼,我們可以遞迴地計算:
分別是截止到當前時刻 t 中、以標簽 1,…,k 為終點的所有路徑的得分指數和。那麼,我們可以遞迴地計算:

它可以簡單寫為矩陣形式:

其中 ,而 G 是對 g(yi,yj) 各個元素取指數後的矩陣,即
,而 G 是對 g(yi,yj) 各個元素取指數後的矩陣,即 ;而
;而 是編碼模型
是編碼模型 (RNN、CNN等)對位置 t+1 的各個標簽的打分的指數,即
(RNN、CNN等)對位置 t+1 的各個標簽的打分的指數,即 ,也是一個向量。式 (10) 中,ZtG 這一步是矩陣乘法,得到一個向量,而 ⊗ 是兩個向量的逐位對應相乘。
,也是一個向量。式 (10) 中,ZtG 這一步是矩陣乘法,得到一個向量,而 ⊗ 是兩個向量的逐位對應相乘。

▲ 歸一化因子的遞迴計算圖示。從t到t+1時刻的計算,包括轉移機率和j+1節點本身的機率
如果不熟悉的讀者,可能一下子比較難接受 (10) 式。讀者可以把 n=1,n=2,n=3 時的歸一化因子寫出來,試著找它們的遞迴關係,慢慢地就可以理解 (10) 式了。
動態規劃
寫出損失函式 −logP(y1,…,yn|x) 後,就可以完成模型的訓練了,因為目前的深度學習框架都已經帶有自動求導的功能,只要我們能寫出可導的 loss,就可以幫我們完成最佳化過程了。
那麼剩下的最後一步,就是模型訓練完成後,如何根據輸入找出最優路徑來。跟前面一樣,這也是一個從 k^n 條路徑中選最優的問題,而同樣地,因為馬爾可夫假設的存在,它可以轉化為一個動態規劃問題,用 viterbi 演演算法解決,計算量正比於 n。
動態規劃在本部落格已經出現了多次了,它的遞迴思想就是:一條最優路徑切成兩段,那麼每一段都是一條(區域性)最優路徑。在本部落格右端的搜尋框鍵入“動態規劃”,就可以得到很多相關介紹了,所以不再重覆了。
實現
經過除錯,基於 Keras 框架下,筆者得到了一個線性鏈 CRF 的簡明實現,這也許是最簡短的 CRF 實現了。這裡分享最終的實現並介紹實現要點。
實現要點
前面我們已經說明瞭,實現 CRF 的困難之處是 −logP(y1,…,yn|x) 的計算,而本質困難是歸一化因子部分 Z(x) 的計算,得益於馬爾科夫假設,我們得到了遞迴的 (9) 式或 (10) 式,它們應該已經是一般情況下計算 Z(x) 的計算了。
那麼怎麼在深度學習框架中實現這種遞迴計算呢?要註意,從計算圖的視角看,這是透過遞迴的方法定義一個圖,而且這個圖的長度還不固定。這對於 PyTorch這樣的動態圖框架應該是不為難的,但是對於TensorFlow或者基於 TensorFlow 的 Keras 就很難操作了(它們是靜態圖框架)。
不過,並非沒有可能,我們可以用封裝好的 RNN 函式來計算。我們知道,RNN 本質上就是在遞迴計算:

新版本的 TensorFlow 和 Keras 都已經允許我們自定義 RNN 細胞,這就意味著函式 f 可以自行定義,而後端自動幫我們完成遞迴計算。於是我們只需要設計一個 RNN,使得我們要計算的 Z 對應於 RNN 的隱藏向量。
這就是 CRF 實現中最精緻的部分了。
至於剩下的,是一些細節性的,包括:
1. 為了防止上限溢位,我們通常要取對數,但由於歸一化因子是指數求和,所以實際上是 這樣的格式,它的計算技巧是:
這樣的格式,它的計算技巧是:

TensorFlow 和 Keras 中都已經封裝好了對應的 logsumexp 函式了,直接呼叫即可;
2. 對於分子(也就是標的序列的得分)的計算技巧,在程式碼中已經做了註釋,主要是透過用“標的序列”點乘“預測序列”來實現取出標的得分;
3. 關於變長輸入的 padding 部分如何進行 mask?我覺得在這方面 Keras 做得並不是很好。
為了簡單實現這種 mask,我的做法是引入多一個標簽,比如原來是 s、b、m、e 四個標簽做分詞,然後引入第五個標簽,比如 x,將 padding 部分的標簽都設為 x,然後可以直接在 CRF 損失計算時忽略第五個標簽的存在,具體實現請看程式碼。
程式碼速覽
純 Keras 實現的 CRF 層,歡迎使用。
# -*- coding:utf-8 -*-
from keras.layers import Layer
import keras.backend as K
class CRF(Layer):
"""純Keras實現CRF層
CRF層本質上是一個帶訓練引數的loss計算層,因此CRF層只用來訓練模型,
而預測則需要另外建立模型。
"""
def __init__(self, ignore_last_label=False, **kwargs):
"""ignore_last_label:定義要不要忽略最後一個標簽,起到mask的效果
"""
self.ignore_last_label = 1 if ignore_last_label else 0
super(CRF, self).__init__(**kwargs)
def build(self, input_shape):
self.num_labels = input_shape[-1] - self.ignore_last_label
self.trans = self.add_weight(name='crf_trans',
shape=(self.num_labels, self.num_labels),
initializer='glorot_uniform',
trainable=True)
def log_norm_step(self, inputs, states):
"""遞迴計算歸一化因子
要點:1、遞迴計算;2、用logsumexp避免上限溢位。
技巧:透過expand_dims來對齊張量。
"""
states = K.expand_dims(states[0], 2) # (batch_size, output_dim, 1)
trans = K.expand_dims(self.trans, 0) # (1, output_dim, output_dim)
output = K.logsumexp(states+trans, 1) # (batch_size, output_dim)
return output+inputs, [output+inputs]
def path_score(self, inputs, labels):
"""計算標的路徑的相對機率(還沒有歸一化)
要點:逐標簽得分,加上轉移機率得分。
技巧:用“預測”點乘“標的”的方法抽取出標的路徑的得分。
"""
point_score = K.sum(K.sum(inputs*labels, 2), 1, keepdims=True) # 逐標簽得分
labels1 = K.expand_dims(labels[:, :-1], 3)
labels2 = K.expand_dims(labels[:, 1:], 2)
labels = labels1 * labels2 # 兩個錯位labels,負責從轉移矩陣中抽取標的轉移得分
trans = K.expand_dims(K.expand_dims(self.trans, 0), 0)
trans_score = K.sum(K.sum(trans*labels, [2,3]), 1, keepdims=True)
return point_score+trans_score # 兩部分得分之和
def call(self, inputs): # CRF本身不改變輸出,它只是一個loss
return inputs
def loss(self, y_true, y_pred): # 標的y_pred需要是one hot形式
mask = 1-y_true[:,1:,-1] if self.ignore_last_label else None
y_true,y_pred = y_true[:,:,:self.num_labels],y_pred[:,:,:self.num_labels]
init_states = [y_pred[:,0]] # 初始狀態
log_norm,_,_ = K.rnn(self.log_norm_step, y_pred[:,1:], init_states, mask=mask) # 計算Z向量(對數)
log_norm = K.logsumexp(log_norm, 1, keepdims=True) # 計算Z(對數)
path_score = self.path_score(y_pred, y_true) # 計算分子(對數)
return log_norm - path_score # 即log(分子/分母)
def accuracy(self, y_true, y_pred): # 訓練過程中顯示逐幀準確率的函式,排除了mask的影響
mask = 1-y_true[:,:,-1] if self.ignore_last_label else None
y_true,y_pred = y_true[:,:,:self.num_labels],y_pred[:,:,:self.num_labels]
isequal = K.equal(K.argmax(y_true, 2), K.argmax(y_pred, 2))
isequal = K.cast(isequal, 'float32')
if mask == None:
return K.mean(isequal)
else:
return K.sum(isequal*mask) / K.sum(mask)除去註釋和 accuracy 的程式碼,真正的 CRF 的程式碼量也就 30 行左右,可以說跟哪個框架比較都稱得上是簡明的 CRF 實現了。
用純 Keras 實現一些複雜的模型,是一件頗有意思的事情。目前僅在 TensorFlow 後端測試透過,理論上相容 Theano、CNTK 後端,但可能要自行微調。
使用案例
我的 Github 中還附帶了一個使用 CNN+CRF 實現的中文分詞的例子,用的是 Bakeoff 2005 語料,例子是一個完整的分詞實現,包括 viterbi 演演算法、分詞輸出等。
Github地址:https://github.com/bojone/crf/
相關的內容還可以看我之前的文章:
中文分詞系列:基於雙向LSTM的seq2seq字標註 [2]
中文分詞系列:基於全摺積網路的中文分詞 [3]
結語
終於介紹完了,希望大家有所收穫,也希望最後的實現能對大家有所幫助。
參考文獻
[1]. 果殼中的條件隨機場 (CRF In A Nutshell)
https://kexue.fm/archives/4695
[2]. 中文分詞系列:基於雙向LSTM的seq2seq字標註
https://kexue.fm/archives/3924
[3]. 中文分詞系列:基於全摺積網路的中文分詞
https://kexue.fm/archives/4195

點選以下標題檢視作者其他文章:
▲ 戳我檢視招募詳情
 #作 者 招 募#
#作 者 招 募#
關於PaperWeekly
PaperWeekly 是一個推薦、解讀、討論、報道人工智慧前沿論文成果的學術平臺。如果你研究或從事 AI 領域,歡迎在公眾號後臺點選「交流群」,小助手將把你帶入 PaperWeekly 的交流群裡。

▽ 點選 | 閱讀原文 | 進入作者部落格
 知識星球
知識星球