生命、宇宙以及任何事情的終極答案，貝葉斯會告訴你嗎？

作者：老喻在加

來源：孤獨大腦（ID：lonelybrain）

01 無意義的混亂

馬斯克格外喜歡科幻小說家道格拉斯·亞當斯的代表作《銀河系漫遊指南》。年少時，他在讀這本書時，就曾嘗試著找到宇宙中屬於自己的位置。從此他就開始了夾生的、癲狂的一生。

作者完全不能預測自己的著作會帶來什麼。就像這本書的初意與馬斯克的感觸截然不同。假如你沒讀過，我們看看故事講的是什麼：

福特·派法特是一位宇宙漫遊研究員，來自參宿四附近的小星球，受僱於銀河系漫遊指南公司，負責從銀河系四處蒐集資料，編輯《銀河系漫遊指南》，但他已經被困於地球15年，直到一天，渥罡人受命負責摧毀地球，用作興建一條超空間快速通道，他藉機搭上便車，同時救走了他的地球朋友亞瑟·丹特。

渥罡人發現了兩人搭上便車，而渥罡人的長官決定將兩人從太空船丟擲氣閘外，一般人在真空的環境下，只能存活三十秒，同時在三十秒被另一艘太空船救起的機會更是數億萬分之一。不過，銀河總統柴法德·癟頭士和他的地球女朋友崔莉恩剛巧偷走了以突破非或然率技術的太空船黃金之心，並駛經兩人被丟擲氣閘的空間，又救起了兩人。

四人駕著黃金之心朝傳說的星球馬格西亞出發，傳說中，馬格西亞是一個替富人興建人造星球的星球，不過宇宙經濟過度膨脹，引發全宇宙的經濟破產。

亞瑟·丹特在馬格西亞上被告知，地球其實只是一個實驗。原來許多百萬年前，老鼠其實是一種超智慧生物，它們建造了一部超級電腦深思，它們問超級電腦，生命、宇宙以及任何事情的終極答案是什麼，經過一段長時間的計算，深思告訴老鼠的後人答案是42，深思解釋它只能計算出答案是什麼，但答案的原因必須由另一部更高智慧的電腦才能解釋，而該部電腦就是地球。

在計算出答案前的5分鐘，地球卻被渥罡人毀滅，地球的全部資料銷毀，老鼠認為僅有的資料寄存在最後離開地球的亞瑟·丹特的腦中，於是決定向亞瑟·丹特開刀做手術。

小說中充滿尖銳的諷刺和隱喻，將整個宇宙的執行看作無意義的混亂，無論是宇宙的哪個維度或時間，這種混亂永不消失，好似一塊五公斤重包裹著檸檬的金磚拍碎了你的頭。

有趣的是，少年馬斯克並沒有看到作者的諷喻，反倒是像謝耳朵那樣看到了別的什麼東西。這一點決定了他日後的軌跡，我們稍晚會說明。

《銀河系漫遊指南》帶給馬斯克最大的感受卻是：提出問題比回答問題更難。

因為我們提出的問題或多或少的都帶有自己主觀或者認知的偏見，所以很難確定自己提出的問題是不是正確的問題。

道格拉斯·亞當斯沒有讓馬斯克成為一個虛無主義者，反倒令他這個無意義的、混亂的宇宙充滿了無盡的好奇。當然，在鋼鐵俠堅定地執行火星計劃時，他個人的人生看起來倒也是無意義、且混亂不堪。理性，激情，應用於計算的邏輯異常複雜，但隱隱約約也可以自圓其說地闡釋一下，後面我會做如此嘗試。

02 宇宙裡的答案

小說裡的“42”是什麼意思並不重要，重要的是這個世界是否存在某個終極答案？

愛因斯坦說：“所有科學中最重大的標的就是，從最少數量的假設和公理出發，用邏輯演繹推理的方法解釋最大量的經驗事實。”

《終極演演算法》的作者佩德羅·多明戈斯教授有一個假設：

所有知識，無論是過去的、現在的還是未來的，都有可能透過單個通用學習演演算法來從資料中獲得。

多明戈斯將該學習演演算法稱為“終極演演算法”。

他認為，如果這種演演算法成為可能，它的發明將成為人類最偉大的科學成就之一。實際上，終極演演算法是我們最不願意發明的東西，因為一旦對其放鬆，它會繼續發明一切有可能發明的東西。

這個世界正在越來越逼近終極演演算法，還是更加遠離？

我們的直覺與此似乎正好相反，我們對發現這個世界的真相的信心不是在增加，而是在衰減。

物理學之父阿基米德曾經豪情萬丈地說：“給我一個支點，我可以舉起整個地球。”

牛頓以其萬有引力和三大運動定律，奠定了此後三個世紀裡力學和天文學的基礎，成為了現代工程學的基礎。

他如同先知般，透過論證開普勒行星運動定律與他的引力理論間的一致性，展示了地面物體與天體的運動都遵循著相同的自然定律。

牛頓樂觀地宣稱：如果一條規律對於所有我們已經見到的事物都成立，那麼這條規律對全宇宙的所有事物都成立。

拉普拉斯寫道：

（牛頓的）《原理》將成為一座永垂不朽的深邃智慧的紀念碑，它向我們展示了最偉大的宇宙定律，是高於（當時）人類一切其他思想產物之上的傑作，這個簡單而普遍定律的發現，以它囊括物件之巨大和多樣性，給人類智慧以光榮。

物理學家、諾貝爾物理學獎得主尤金·維格納，則驚嘆“數學在自然科學中不可思議的有效性”：

由少量的觀察推匯出規律，是什麼神奇的力量讓這些規律可以運用到超出其預測範圍的領域？

03 求解世俗世界

讓我們回到世俗世界。

並非只有數學家、物理學家、以及科幻迷們才致力於追求“生命、宇宙以及任何事情的終極答案”。

人們不同程度地試圖找尋“終極答案”，只是落在不同的問題設定上。作為個人主義者，我會將話題引向偏於個人的終極答案。

就像達利歐在《原則》裡嘗試做的。他說自己一生中學到的最重要的東西，是一種以原則為基礎的生活方式，“是它幫助我發現真理是什麼，並據此如何行動。”

這本書的英文書名“Principles”，可以翻譯為“原理、原則、法則、主義、本質、源泉、根源”等等。我們可以理解作者希望表達的不會少於這些可能的中文涵義。

甚至野心更多。牛頓於1687年7月5日出版的徹底改變世界的《自然哲學的數學原理》（現常簡稱作《原理》），英文書名叫《Mathematical Principles of Nature Philosophy》，後來經常就被簡稱為《Principles》。

投資家成功後琢磨“本質問題”，未嘗不是值得鼓勵的好事，好過他們胡乾別的什麼拯救世界的事情。

在導言裡，達利歐寫下了自己的原則總綱：

1. 獨立思考並決定：（1）你想要什麼；（2）事實是什麼；（3）你如何實現。

2. 以可信度加權的方式做決定。

3. 遵照原則做事。

4. 以系統化的方式來決策。

為什麼要重溫這本“過時”（按照現在的所謂知識更新速度，即使如此乾貨的暢銷書，不用幾個月就有點兒人老珠黃了）的書？

達利歐是頂尖的聰明人，他在《原則》一書中，半個公式都沒用。據統計，假如一本書或者一篇文章，每用一個公式，閱讀量就會掉多少個百分點。

另一方面，達利歐可能有如下假設：

1. 懂公式的人，無需列出公式，他們也明白是啥意思；

2. 不懂公式的人，列出來也沒用，乾脆就讓他們當雞湯看假裝懂懂就好了。

下麵讓我們看看，達利歐預設讀者該知道哪些公式。

04 聰明太多，懷疑太少

達利歐畢業於哈佛商學院，透過案例教學法，接受了世界上“最好的”教育。不用說，他有理論、懂計算、曉實戰，對於“期望值計算”這類基本功，當然瞭然於胸。

何謂期望值計算？舉例如下：

塔勒布在投資研討會說：“我相信下個星期市場略微上漲的機率很高，上漲機率大概70%。”但他卻大量賣空標準普爾500指數期貨，賭市場會下跌。他的意見是：市場上漲的可能性比較高（我看好後市），但最好是賣空（我看壞結果），因為萬一市場下跌，它可能跌幅很大。 

分析如下：

• 假使下個星期市場有70%的機率上漲，30%的機率下跌。

• 但是如果上漲只會漲1%，下跌則可能跌10%。

• 未來預期結果是：70%×1%+30%×（-10%）=-2.3%。

• 因此應該賭跌，賣空股票盈利的機會更大。

如芒格所言，巴菲特每天做的，都是算這個簡單數學問題。與其說是一種數學能力，不如說是一種思維樣式。知道容易，做到極難。

1982年8月，墨西哥對其債務違約。因為美國銀行正在向像墨西哥一樣高風險的其他國家提供貸款，總額約為其資本金總和的 250%。美國的商業貸款活動逐漸陷於停頓。

達利歐是少數預見到這一情況的人，他預測美國正在走向一場蕭條，儘管美聯儲增加了貨幣供給，令股市出現了創紀錄的漲幅。

達利歐將這一現象解讀為市場對美聯儲行動的條件反射式反應。並取用了歷史：在 1929年，股市上漲 15%之後，就出現了史上最大規模的崩盤。

與索羅斯和塔勒布一樣，達利歐是個將理論與認知付諸行動的人，他計算如下：

• 美聯儲的努力失效，經濟走向崩潰的機率是 75%；

• 美聯儲的行動一開始成功刺激經濟，但最終仍然失敗的機率是 20%；

• 美聯儲提供了足夠的刺激來輓救經濟，但最終觸發惡性通脹的機率是 5%。

作為計算的結果，為了透過對沖規避最不利的可能性，達利歐開始買入黃金和國債期貨，作為對歐洲美元的對沖，這是一種押註於信貸問題加劇的風險控制方式。

看起來，這個推理毫無漏洞。

然而，達利歐錯了。錯得虧光了整個公司。

原因我們姑且不說了。總之，即使達利歐預測的那部分全都對了，但是連鎖反應中任何一個環節的波動，都可能令推理失效。美元迴流導致的升值壓力，令美聯儲降息，驅動了一場意外的經濟繁榮。

在我看來，年輕的達利歐犯了三個錯誤：

錯誤1、正確太多。在哈佛商學院的精英教學體系裡，他一直在學習“如何做對一件事”，他們聰明而自信，志在必得。然而，在一個複雜系統裡，做對、並證明自己正確，經常是危險的；

錯誤2、懷疑太少。現實世界裡，他沒能保持足夠的自我懷疑。休謨在《人性論》以及後來的《人類理解研究》中反駁了“因果關係”具有真實性和必然性的理論，他指出雖然我們能觀察到一件事物隨著另一件事物而來，我們並不能觀察到任何兩件事物之間的關聯。

錯誤3、自我高估。個人世界裡，他高估了自己的專業和判斷。在卡尼曼的研究裡，對自己的高估外加對外部意見的低估，令我們的決策判斷遠沒自以為是的那麼靠譜。

05 試錯和可證偽

埃皮克提圖說：一個人不可能重新認識自己認為已經瞭解的事物。

人類的大腦天生就有一種儘快作出決定，以此消除懷疑的傾向。

另一方面，人們喜歡發現、或者製造“因果關係”。

在《人類理解論》一書中，休謨主張所有人類的思考活動都可以分為兩種：

追求“觀唸的連結”（Relation of Ideas）與“實際的真相”（Matters of Fact）。

前者牽涉到的是抽象的邏輯概念與數學，並且以直覺和邏輯演繹為主；後者則是以研究現實世界的情況為主。而為了避免被任何我們所不知道的實際真相或在我們過去經驗中不曾察覺的事實的影響，我們必須使用歸納思考。

伯特蘭·羅素將休謨視為是實證主義者，認為知識只有可能是從對於事件的觀察上衍生而出—從“對感官的印象”或是“感覺的資料庫”裡得出，同時其它任何不是透過觀察經驗而得的知識都是“毫無意義的”。

波普爾認為可證偽性是科學的不可缺少的特徵，凡是不可能被經驗證偽的命題，如本體論問題、形而上學問題、數學和邏輯上的重言式命題、宗教、神學和占星術都屬於非科學。

試錯法屬於證偽主義。可證偽性，又稱可反證性、可否證性，在科學和科學哲學中用來表示由經驗得來的表述所具有的一種屬性，即“這些結論必須容許邏輯上的反例的存在”。

索羅斯和塔勒布都是波普爾的信徒。塔勒布寫道：

雖然索羅斯在他寫的文章中沒有明白表示，但他懂得怎麼處理隨機性，方法是保持批判性的開放心胸，而且不以改變看法為恥。他到處宣稱自己容易犯錯，卻仍擁有那麼強大的力量，因為他曉得本身的缺點，其他人卻自視甚高。他瞭解波普爾，也過著波普爾式的生活。

波普爾表示，科學並不像錶面上看到的那麼嚴肅，世界上只有兩類理論：

1. 經過檢驗並以適當的方法予以駁斥、已知為錯誤的理論，稱之為已被證偽（已遭否證falsified）。

2. 尚未得知錯誤或者尚未遭否證，但將來有可能被證明為錯誤的理論。

塔勒布對此解釋道：

為什麼沒有一個理論正確？因為我們無從得知是否所有的天鵝皆為白色。其中使用的檢驗機制可能有誤，但是我們仍舊可以提出這樣的陳述：世界上有黑天鵝。

理論無法被驗證，只能暫時被人接受。以棒球教練貝拉的話來說，過去的資料裡面有很多好東西，可惜的是它也有壞的一面。落在這兩類理論之外的，就不叫理論。

如果一個理論沒有包含一組可以被檢證錯誤的條件，只能稱之為騙術——否則無法加以駁斥。

為什麼？因為占星家總是能夠找到理由去解釋過去的事件，比如說“火星線上上但運勢不太強”。同樣的，在我看來，如果沒有什麼事情能夠改變一位交易員的看法，那麼他就稱不上是交易員。

牛頓物理學和占星術的差別說來諷刺。牛頓物理學是科學，因為它允許我們證明它是錯誤，而且確實已被愛因斯坦的相對論推翻了；然而占星術卻不能被證明錯誤，因為它沒有提供條件讓我們駁斥它。

這一點成了判別科學和胡說八道的基礎，稱做“畫界問題”（the problem of demarcation）。

塔勒布對波普爾下麵的名句推崇備至：

這些人有大膽的觀念，卻對本身觀唸的批判不遺餘力；他們設法要瞭解自己的觀念是否正確，使用的方法是先瞭解它們是否可能無誤。他們大膽推論，然後極力嘗試推翻本身的推測。

他認為，“這些人”指的是科學家，但也可能是任何人。

以上這些“誇誇其談”的理論到底有什麼用呢？

很有。

我們的文化喜歡以“到底有什麼用”來評判一個東西是否有價值。下麵我來解釋一下“證偽”這個東西可以有什麼用。

題目：最少翻動的次數

桌上放著四張紙卡，分別寫著1、2、3、4 (如下圖)：

有人說：“1的背面都寫著2。”

請問：你要將幾張牌卡翻開才能驗證這個說法是否正確呢？

你可以用手矇住這裡想一下，然後再往下看。

答案是：

3張。

為什麼呢？

• 要翻開“1”確認背後是“2”，要翻開“3”、“4”確認背後不是“1”，以上都符合時，該說法才是對的。

• 至於“2”就不用翻開了，因為它背後不管是多少都不影響那句話的正確性。

如果用“證偽”的方法，就更容易理解了。其實，這也正是“逆向思維”的精髓所在。倒過來想，怎樣才能證明這個說話是錯誤的呢？如果無法證明是錯誤的，自然就是正確的了。

NND，我又不參加奧數，這種小伎倆有個鳥用？

讓我們再來一題。

題目：找規律

給你三個數字 2 , 4 , 6，請找出該序列中的潛在樣式。

條件：你可以提出其他幾套包含三個數字的序列 ，並將獲知它們是否符合這種樣式。例如你可以問，8，10，12，這三組數字符合該樣式嗎？

這看起來是一道簡單得有詐的幼兒園大班題目。難道不就是“偶數 、升序數和連續數”嗎？又或者是2的連續數倍數？

這是《做最好的決策》裡的一道題。沃頓教授休梅克寫到：

形成某種假設通常是個好主意 ，特別是如果有很多假設可以得到實證檢驗的話 。但是 ，當人們真正制定策略來檢驗他們的假設時 ，一種暗中為害的確定性偏見可能會乘虛而入。

不知道你是否和大多數人一樣，傾向於檢驗適合他們規則的序列。如下表的 “檢驗一個假設 ”一欄中所示 （對於每個測試序列是否符合 “ 2 , 4 , 6 ”這組數字的隱含樣式這個問題 ，該表中作出了是或不是的回答 ） 。 

書中寫道，經過三次成功測試之後 ，參與者通常會自信滿滿地說 ， “偶數 、升序數和連續數 ”的假設是正確的 。但他們錯了 。

可以考慮用一種替代方法來檢驗違反假設的序列 （如第四行所示 ） ——換言之 ，就是故意犯錯 。如果參與者選擇了不符合他們當前假設的數字 ，他們通常會更快地發現 ，真正的樣式是任何升序數 。

這種樣式很少被髮現 ，除非被試者願意犯錯 ——也就是說 ，願意去測試那些違揹他們信念的數字 。相反 ，大多數人陷入了一種狹隘的錯誤假設 ，正如現實生活中經常發生的那樣 。如此一來 ，他們唯一的出路是 ：犯一次錯誤 ，並且證明這終究不是個錯誤 。

（註：也許有另外的潛在樣式，例如：任何不降序的三個數字。在此我們稍微跳過。）

你必須採用“試錯法”。如作者所說，有時 ，犯錯不僅是得到正確答案的最快方法 ，也是唯一方法 。

參與這項實驗的大學生，僅10%的人發現了“正確”樣式 。

絕大多數人則被困在一種狹隘的假設中 ，例如偶數和連續數 ，而且他們只去測試符合這一樣式的數字組合 。從短期來看 ，他們使用這種方法是正確的 。但從長遠來看 ，他們錯了 ，因為他們並沒有透過足夠廣泛的實驗來發現這種潛在樣式 。

不論什麼時候 ，只要你沒有多少確鑿的證據 ，你在探討自己關於各個部分如何組合在一起的最初推測時 ，你的正確率就不高 。找出這種樣式的最快方法 ，就是去嘗試很多否定性測試 。

簡而言之，證明“所有的天鵝全都是白色的”，不是去找更多的白天鵝，而是要去找究竟有沒有黑天鵝。

王爾德說：“想象是模仿，批判的精神才具有創造力。”在數字時代，在金融時代，在複雜時代，試錯和證偽，是弄潮兒們的利器。

如此一來，我們就不難理解，達利歐在《原則》一書的“導言”開頭就寫到：

在我開始告訴你們我的思考之前，我想先說明，我是個“愚人”，相對於我需要知道的東西而言，我真正知道的並沒有多少。

不管我一生中取得了多大的成功，其主要原因都不是我知道多少事情，而是我知道在無知的情況下自己應該怎麼做。

我一生中學到的最重要的東西是一種以原則為基礎的生活方式，是它幫助我發現真相是什麼，並據此如何行動。

06 從直覺到演演算法

猶太人了不起的地方在於，即使命運多舛，他們仍然能夠去思考人類自身的那些終極問題。

索羅斯和卡尼曼都曾在二戰時期，東躲西藏、四處逃命。手無縛雞之力的卡尼曼，在建國之初的以色列，又經歷了獨立戰爭的炮火。

在軍營中，年輕的卡尼曼“發明”了一套演演算法，用於軍隊的面試，令效果大為改觀。四五十年後，他已經榮獲諾貝爾獎，回到軍營參觀，發現自己當初的“演演算法”仍在高效執行著。

那套演演算法和下麵要提及的阿普家評分原則一樣簡單，卻遠比軍官的經驗和直覺更加靠譜。

我們滿心相信這個世界是有意義的，這份信心建立在一個穩妥的基礎之上：我們最大限度地忽略自己的無知。 

丹尼爾·卡尼曼如是說。

專家是靠不住的，直覺是靠不住的，你我都是靠不住的。

卡尼曼發現，應用資料統計方法得出的結果，經常比專家的預測結果要準確得多。

更新研究則更深入地指出：均衡考慮各項預測因素的公式更有優勢，因為它們不受樣本突變的影響。

這種基於等權原則的計算方案的成功有著重要的實踐意義：它可以在不作任何事前統計研究的基礎上就能開發出有用的運算方法。

這種基於現有資料或者常識的簡單等權公式通常可以預測出意義重大的結果。

在《思考，快與慢》一書中，卡尼曼舉了下麵這個非常生動的例子：

一項拯救了千萬嬰兒的簡單運演演算法堪稱對於這項研究的經典應用。婦產科醫生清楚地知道，如果嬰兒在出生後的幾分鐘內無法正常呼吸的話，他/她就會有很大的腦損傷甚至夭折的風險。

在 1953年麻醉學家弗吉尼亞·阿普加（Virginia Apgar）介入之前，內科醫生和接生人員一直在用他們的臨床經驗來判斷嬰兒是否處於危險狀態，不同人員的依據也不盡相同。一些人側重於觀察孩子的呼吸情況，另一些人則觀察嬰兒的啼哭頻率。由於沒有一個標準，人們經常錯過危險訊號，導致許多新生兒不幸夭折。

一天早飯後，一個住院醫生問阿普加醫生如何對新生兒作系統評估。她回答道：“這很簡單，你可以這樣做。”阿普加快速寫下了 5個變數（心率、呼吸、反應、肌肉強度和顏色）以及 3個分數（0、 1、 2分別代表各個變數的穩健度）。

阿普加意識到自己可能會有所突破，而且這一突破還可能被應用到所有的產房中，她便開始用這種方法評估每一個出生一分鐘的嬰兒。一個得到 8分以上的嬰兒一般是膚色粉紅、蠕動、啼哭、面部扭曲並擁有 100次以上的脈搏，這樣的嬰兒外形很好。低於 4分的嬰兒一般是渾身青紫、肌肉鬆弛、不愛動且心跳微弱，這樣的嬰兒需要立即救治。

應用了阿普加的評分原則後，產房的護士們終於在判斷嬰兒情況是否危險的問題上有了一套標準，人們認為這個公式對減少嬰兒的夭折率起到了很重要的作用。現在，阿普加的方法依然應用於每一個產房中。

阿圖爾·甘德（ Atul Gawande）近期的著作《一份清單宣言》（ A Checklist Manifesto）也介紹了一些其他案例，以說明串列以及簡單原則的優點。

行文至此，讓我們回到開頭的《原則》裡的四個基本原則中的兩條：

1. 以可信度加權的方式做決定。

2. 以系統化的方式來決策。

關於第一條，可信度加權，我們在後面的決策樹裡會介紹類似的方法。

達利歐強調道：

• 我犯下的代價慘痛的錯誤使我改變了看問題的角度，從“我知道我是對的”變成了“我怎麼知道我是對的”。

• 這些錯誤讓我養成了謙遜的習慣，我需要用謙遜平衡我的勇敢。

• 我知道我可能會錯得離譜，又好奇為什麼其他聰明的人對事情的認識與我不同，這促使我既從自己的視角看問題，也從別人的視角看問題。

• 這讓我看到了很多維度，如果我只從自己的視角看問題，是看不到這麼多的。

• 我懂得瞭如何對不同人的觀點進行加權，從而選擇最好的觀點，也就是說，我用可信度加權的方式做決定。

• 這降低了我犯錯誤的可能性，真是太棒了。
  

那個從哈佛畢業的、差點兒被墨西哥債務違約擊垮的自信青年，現在已經是一位老到的、“我可能錯了”的、休謨與波普爾的信徒。

而關於第二條，則是達利歐認知更新後的行為更新。其策略是：

• 以演演算法的形式把決策標準表達出來，把這些演演算法植入計算機。

• 進而以此提高集體決策質量。這樣的決策系統（尤其是在實踐可信度加權的情況下）是極其強大的。
  

我將此描述為：

年輕時的達利歐已是一名超級球員，他對點狀的機率計算滾瓜爛熟，但很多時候卻不能應對複雜環境下的挑戰；

後來，他變成一名超級教練。球隊靠系統，而非超級球員來贏得一場球賽；

再後來，他還會成為一名超級經理。

07 決策高手

富蘭克林說：人，在二十歲，意志支配一切；三十歲，機智支配一切；四十歲，判斷支配一切。

我們並非是命運的產物，而是命運降臨之後我們的決策與行動的產物。

無論多麼擅長計算，如果不能做出決策，採取行動，毫無意義。

有兩種思維樣式：決策和行動。

只有資源不可撤銷地分配到行動中，決策才算是真正完成了。因此，我們需要付諸行動，並且思維從思考樣式轉換為行動樣式。

絕大多數人在絕大多數時候，只是踩著西瓜皮做決定，其實放棄了決策的權力。

就像《解憂雜貨店》所寫：

其實所有糾結做選擇的人心裡早就有了答案，諮詢只是想得到內心所傾向的選擇。最終的所謂命運，還是自己一步步走出來的。

有些知識即使知道了也毫無用處，如果不知道就會很慘。例如下麵幾點：

1. 內控點

德國籍猶太人早在 20世紀初於柏林提出了“格式塔心理學”理論，目的是以科學的方式去探索人類思維的謎團。

《思維簡史》一書介紹道：

格式塔心理學家在揭示思維的有趣現象並將其巧妙呈現出來這一方面做出了極大的貢獻——就好似暗夜中射出的一道微光，漸漸點亮了天空。

灰色在被紫色包圍時看起來像綠色，被藍色包圍時則顯得像黃色。如果你對別人喊：“別踩那隻香蕉蟲！”他一定以為你喊的不是“蟲”，而是“皮”。

格式塔心理學家認為，在外部刺激與由此引起的人的內部感覺之間，並不存在必然聯絡，因為人的思維會以多種稀奇古怪的形式介入這個過程。

形象地說，就是在外部世界對你施加的影響，以及與你內心的感受之間，應該預留一個緩衝空間。你要在這部分空間裡，進行自己的決策。否則，你就活得如同一隻驚弓之鳥。

芒格說：“宏觀是我們要承受的，微觀才是我們有所作為的地方。”

2. 決策框架、流程、要素

《斯坦福商業決策課》裡說：

決策是我們塑造未來的最強大的技能，做出良好決策是讓人生最大限度地滿足我們期望的關鍵。要在行動之前判斷決策質量，我們需要明白決策的本質內涵。

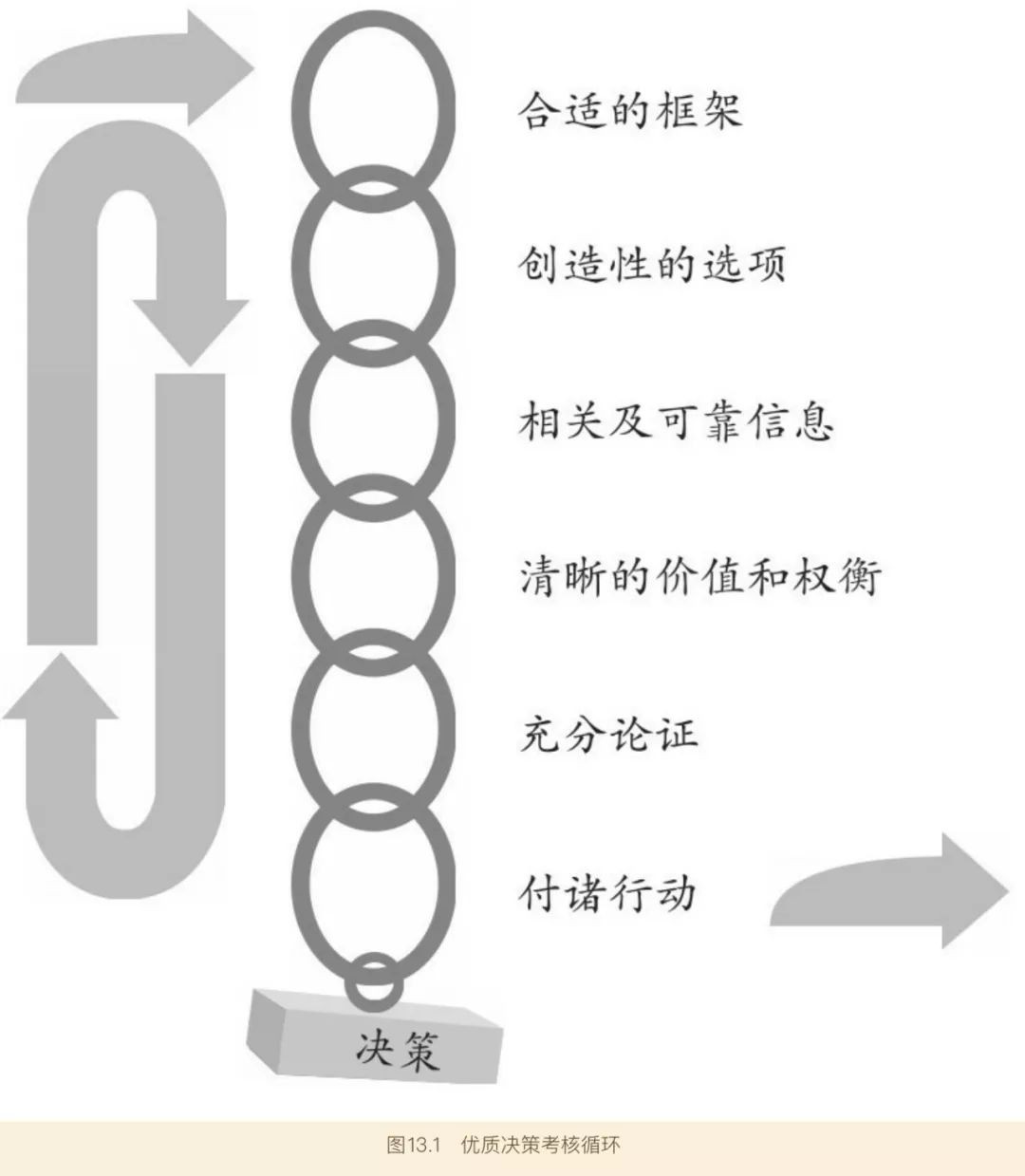
該書認為，每個決策都可以劃分為六個不同要素，每個要素都必須高質量地解決。這就是優質決策的六大要素：

（ 1）合適的框架；

（ 2）創造性的選項；

（ 3）相關及可靠資訊；

（ 4）清晰的價值和權衡；

（ 5）充分論證；

（ 6）付諸行動。

3. 決策樹

《不確定世界的理性選擇》裡寫道：

我們會運用“決策樹”這樣的圖解形式來描繪決策情境。這些圖解的主要作用之一是對個人或公眾決策情境中的一些要素進行總結，以便於將科學決策理論所涉及的一些原理加以運用，從而選擇最佳行動方案。

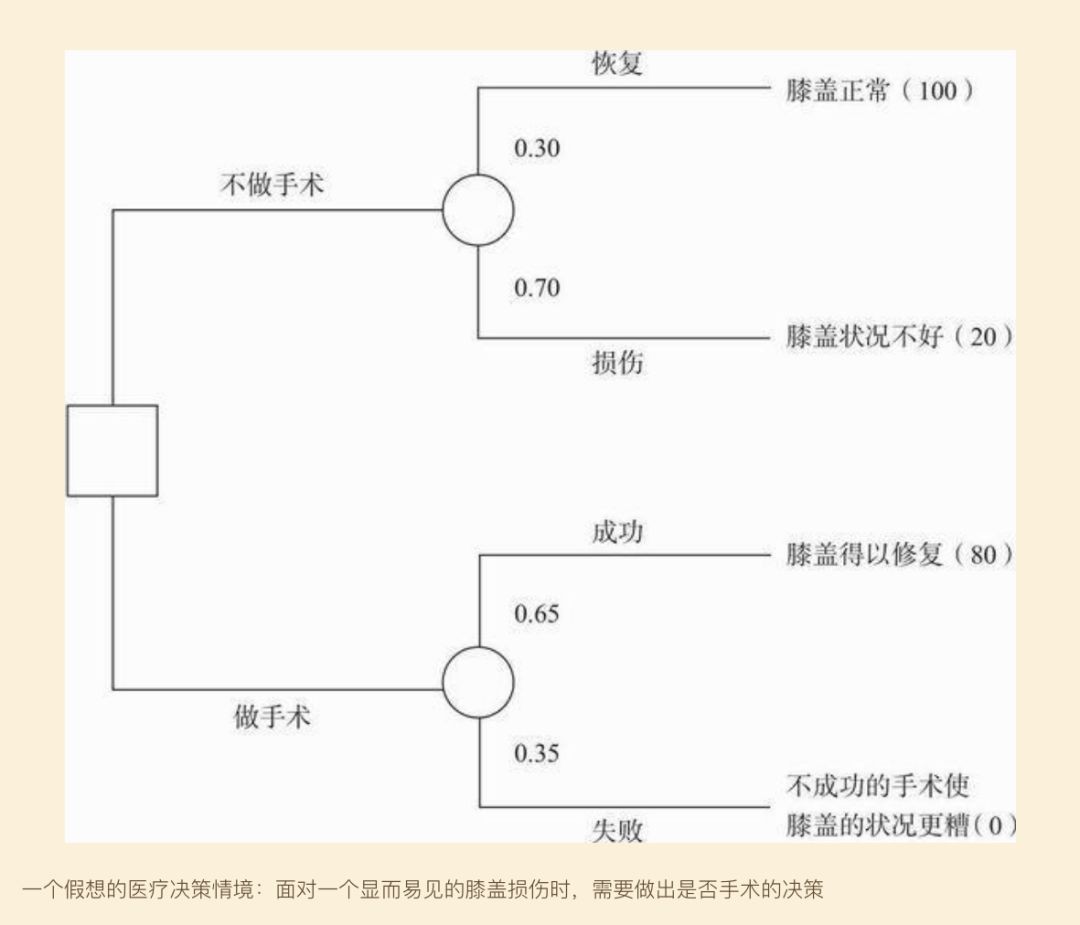
決策樹狀圖有一個約定俗成的慣例：我們用一張佈滿選擇點和結果的假想地圖來表示情境，這些選擇點和結果會導致相應的後果，就像道路上表示岔路口的路標以及沿路的各種事物。

在圖解的最右邊，我們列出了可能的後果，這些後果都是和決策樹中的選擇點以及相應事件相聯絡的。我們將會用一些數字來概括決策者對於相關結果的評估（它們在傳統意義上被稱為“效用”，但我們更願意稱之為“個人價值”）。

在本文“四”計算期望值的例子裡，也可以用決策樹的形式進行表達。

4. 勇敢地做決定

除了投資，絕大多數情況下，隨便做個決策都好過沒有決策。

如查蘭所言：你需要強大的內心，對於真正有意義的事，你要鍥而不捨地施加你的影響力，還要有足夠的想象力來尋找新方案。別怕得罪人，勇敢地表達你的主觀判斷。別怕，要勇敢做艱難決定。

以上這些算是“決策”的基本動作。下麵，則是高手的自選動作。

5. 修剪決策樹

影響一件事情的因素可能會很多。但是在決策樹中，羅列過多選項，意義並不大。專家的建議是控制在6、7個以內。

曾有研究表明，頂尖職業棋手和普通棋手的計算速度差別並不大，但前者修建決策樹更富有效率。

在一篇標註“原文/ Farnam Street”的譯文裡，有如下精彩論述：

我們通常認為收集盡可能多的資訊將有助於我們做出最佳決策。有時候這是對的，但有時候這反而會拖累我們的進度。在某些情況下，它甚至會非常有風險。

許多頂尖的成功人士會採用簡易而且通用的啟髮式決策法，以便省去針對單獨情況的思考。

啟發法（heuristics）是指依據有限的知識或不完整的資訊在短時間內找到問題解決方案的一種方法。

• 對史蒂夫·喬布斯而言，啟發法的預設樣式也許是“說不”。

• 對沃倫·巴菲特而言，是對任何需要計算器或電腦輔助的決策“說不”。

• 對埃隆·馬斯克而言，啟發法可能意味著從第一性原理*開始推演。

• 亞馬遜的創始人傑夫·貝佐斯為我們提供了另一個可以借鑒的決策方法。他會先問自己，這是一個可逆決策還是不可逆決策？

喬布斯的原則是不要第二選項，他甚至不要廣告公司拿出候選方案，而是把第一套方案做到極致。當然，iPhone照樣是要有不少原型機的。

簡而言之，喬布斯如同屠夫一般修剪決策樹。

巴菲特天生就是個計算機。假如他的人肉計算機沒算清晰，還要開啟電腦算一下公司的未來現金流折現是多少，那就太不堪了。

而在貝佐斯看來，如果決策是可逆的( reversible)，即使沒有十全的資訊，我們也要當機立斷。如果決策是不可逆的( irreversible)，那麼我們最好三思而後行，確保考慮足夠充分的資訊，並盡可能透徹地審視問題後再行動。

貝佐斯利用這種啟發法做了創立亞馬遜的決策。他認識到，亞馬遜就算失敗了，他也能重回之前的崗位。他仍可以從失敗中學到很多，並不會因此後悔。他敢於冒險，因為這項決策是可逆的。啟發法很好地為他所用，並長期為他的決策提供指導。

可逆的那部分，高手們有“系統動力學”與“貝葉斯公式”。

6. 機率化的思考與行動

在決策樹上，各種情境被賦予的數值是機率化的，期望值也是機率化的，最終計算也是機率化的。

對於決策高手而言，要把好的結果和明智的決策分開。什麼意思呢？就像職業球手，認真打好每個球（決策），而不會受到比分（結果）的影響。

進而言之，即使我們竭盡全力做對了大多數事情，仍然未必有好的結果。

7. 在無知的情況下決策

《賦能》一書，探討了複雜環境下的組織變革。作者寫道：

2002年2月，美國國防部舉行新聞釋出會，申明目前還沒有證據表明伊拉克擁有大規模殺傷性武器。當時的美國國防部部長唐納德·亨利·拉姆斯菲爾德打趣地說了一句流傳甚廣的“金句”：

“如我們所知，有些是‘已知的已知’，即有些事我們知道自己知道；我們同樣知道，也有些是‘已知的未知’，也就是說有些事我們知道自己不知道。但還有些事是‘未知的未知’，即我們並不知道自己不知道。”

在無知的情況下，我們如何做決策？本文已經提及了：

• 機率化思考；

• 應用演演算法；

• 打造應對不確定性的敏捷團隊。

以及後面要提及的：系統動力學、混合演演算法、貝葉斯法。

對付不確定性，塔勒布採用的是槓鈴策略，一方面是因為他從事金融行業（按下鍵盤做決策），一方面是因為他是個捕鯨者（期貨交易，等待大機會）。

但在現實中，絕大多數人都是捕蝦者，而且需要物理意義上、更高頻地勞作，該怎麼辦？

08 系統動力學&混合演演算法

1. 連續決策

決策樹？太理想化了，誰會用決策樹來選擇老婆老公？

裝腔作勢地在PPT上畫一堆嚇死人的圖表，我們腦海中就浮現出麥肯錫之類。馬雲們對他們也滿是嘲諷。

那些排行榜上的老闆們，例如碧桂園的楊國強，難道還會用決策樹嗎？

我的回答是：

超級決策者們即使不畫出決策樹，甚至不懂決策樹，但他們天生就是決策樹修剪高手。

上面沒有提及、現實中也經常被我們忽略的是：

無論工作還是生活，並非是有一個決策問題，被洗得乾乾凈凈地擺在盤子裡，讓你拿刀叉來解決。

現實中，我們面對的，往往是“連續決策”的難題。

這類連續決策難題，有些是不可逆的，表現為“我這輩子真倒黴”式的一個又一個意想不到的麻煩事兒；有些則是貝佐斯所說的“可逆”的決策，這次不行下次再來。

2. 系統動力學

在《麻省理工深度思考法》一書裡，作者講了自己在MIT的一次經歷。教授列舉出兩家有競爭關係的企業 ，讓大家進行討論 ：

A公司和B公司是兩家勢均力敵的檢測儀製造商。 

A公司的產品包裝獨特、設計新穎；B公司的產品樣式簡單粗糙 ，能看見配管 、感測器等內部構造 ，兩家公司的產品效能及價格等幾乎沒有差別 。

教授當時提出了這樣的問題 ：

 “ 5年後 ，哪家公司會得到更大的市場份額 ？ ”

看起來答案應該是A吧 。

然而 ，正確答案是B公司 。 

為什麼呢？

• B公司產品能看見內部構造 ，使用者可根據自身使用需求進行加工 。

• B公司也透過學習吸收這些顧客公司的加工 ，推出相應的新產品 ，形成了一個良性迴圈 。結果 ， B公司在顧客自身加工的基礎上改良產品 ，讓使用者體驗變得更好。

• 反觀A公司 ，用華麗的外表設計掩蓋了本質性的東西。

反饋是冠軍的早餐。——肯.布蘭查德

作為MIT的明星課程，系統動力學的立場是：

不囿於錶面現象及細枝末節 ，發掘事物背後隱藏的模型及動力機制 。

作者認為，系統動力學是透過隱藏於現象背後的 “模型 ”及 “動力機制 ”去捕捉本質的綜合學科，如下圖：

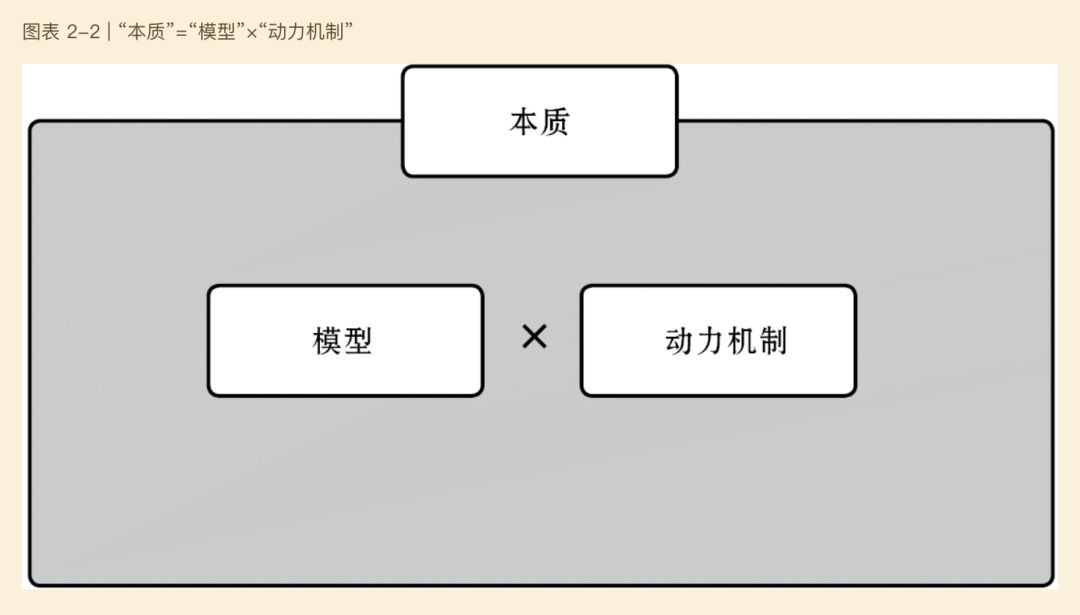
模型，是指產生某種現象的結構 ，包括構成要素及其相互關係 。

動力機制，是以長遠目光觀察模型產生的現象 ，以及今後將會產生怎樣的結果及動向 ，即會出現怎樣的樣式 。

系統動力學強調：不還原要素 ，從全域性捕捉。

以往的科學方法論註重的是要素還原主義 ，而系統動力學則是基於俯瞰全域性的角度。這有點兒像圍棋的區域性計算與大局觀的關係。

不過，阿爾法狗的大局觀那麼厲害，也仍然屬於某種“還原主義”，這裡我們先不岔開去細究了。

一句話，決策樹試圖透過建立演演算法框架，去除非理性的影響，來進行判斷和決策。

而系統動力學，則透過“全域性觀（模型）+動力機制+反饋系統”，來發掘 “條理清晰的答案 ” 。

3. 混合演演算法

超級決策者厲害的地方在於整合決策的能力。決策樹在他們那裡，變成了一個“系統動力學”。

一個機構是“死”的還是“活”的，或者“活”得怎麼樣，取決於“系統動力學”執行之狀況。

就像一輛車。有的車昂貴、豪華，但跑不起來；有得車跌跌撞撞，卻能開去西藏。

如此我們便很容易理解：

為什麼後期的雅虎，看似也有一手不錯的牌，就是打得一塌糊塗；

為什麼亞馬遜、今日頭條等公司業務紛雜，卻有清晰的“飛輪效應”。

極少有CEO是系統工程學高手。我稱之為“混合演演算法”，即：將技術、商業、社會、願景、人性、市場中的不同變數，代入一個簡潔完整的方程式，進行快速、銳利的決策。具備這類能力與天賦的CEO極少。

混合演演算法+系統動力學=“飛輪效應”。偉大的公司都有明晰、可見的飛輪。不管規模多大，業務多複雜，都表現為聚焦、緊湊，擁有“單一”式的敏捷，如滾雪球般快速增長，並以反饋系統，具備自我更新、以及反脆弱的能力。作為結果，這些公司多為輕資產，利潤率高，現金流極好。

混合演演算法高手，懂得“複雜理論+機率思維”。他們經常認為自己的成功是因為運氣好，而非自誇神勇。他們相信“湧現”，而非宏大的無所不能者。這要求決策者既要著眼長遠（有點兒牛頓力學式的），又要能夠忍受眼前的混亂（有點兒量子力學式的）。

除此之外，還需要：演化與自我掃清。運氣，執行力，學習力，缺一不可。並且成為企業文化的一部分，如貝佐斯所言，可傳染、可習得。

09 了不起的貝葉斯

1. 拉普拉斯妖

拉普拉斯被認為是因果決定論的信徒。

儘管被譽為法國的牛頓，拉普拉斯並不像牛頓那樣信奉上帝。牛頓偉大的計算有賴於“上帝存在”這個前提。例如在太陽系，各個行星及其衛星的運動既受太陽的制約，又以難以捉摸的多種方式彼此互相影響。牛頓認為要使這一複雜的系統免於陷入混亂，需要有上帝的不時幹預。

當拿破侖看到拉普拉斯的鉅著《天體力學》時，問他為何不提上帝。拉普拉斯明確地回答：“陛下，我不需要那個假設。”

拉普拉斯在1814年提出假定：有一個智慧生物能確定從最大天體到最輕原子的運動的現時狀態，就能按照力學規律推算出整個宇宙的過去狀態和未來狀態。

這就是著名的“拉普拉斯妖”。作為預言先知，它傳承畢達哥拉斯的“萬物皆數”理論，能透過牛頓的簡單公式輕易計算出宇宙中某個原子的過去和未來。

後來，這隻物理學上著名的怪獸，被量子力學打敗了。

可我們忽略了拉普拉斯對機率和統計學的巨大貢獻，而機率正是量子力學時代的救命武器。

拉普拉斯給出了一個古怪的關於太陽會升起的機率的方程，他聲稱這個機率是(d+1)/(d+2)，d是過去太陽升起的天數。拉普拉斯聲稱這個公式可以應用於所有我們不認識的事物上，或是在我們已知，但由於我們不知道的事物而陷入泥潭的事物上。

塔勒布在他的書中，很隱蔽地盜用了拉普拉斯俏皮而智慧的、對“已知的未知事物”的機率預測，即，存在可很久的事物，未來會繼續存在那麼久。所以他只喝幾千年前的飲料，只看經典之作，等等。

然而，如前所述，塔勒布是休謨和波普爾的信徒。而在“因果論”這一點上，拉普拉斯與休謨貌似屬於“敵對陣營”。

又或者說，敵對陣營彼此間經常是犬牙交錯、相恨相愛的。

2. 牧師貝葉斯

有些人一生就是為一件事而來。

託馬斯・貝葉斯，英國人，生於 1702年，曾在愛丁堡大學學習神學和數學。後來成為一名牧師。

貝葉斯一生中僅寫過一篇數學論文，題為《關於機率思考中某一問題的解法的考察》。他試圖以此證明上帝的存在，也許是因為不太有信心，貝葉斯將其擱置一旁。

貝葉斯去世後，他的朋友理查德・普萊斯整理了他的論文，於 1764年發表於皇家學會的《哲學紀要》。

一直在進行類似研究的拉普拉斯，註意到貝葉斯的成果。1781年左右，拉普拉斯將貝葉斯對“逆機率”的理解，整理為沿用至今的公式：

沒人能想到“簡單的”貝葉斯公式有如此強大的力量。

這個公式對人類的個人決策和公共生活都帶來了巨大的影響。

重溫一個著名的題目：

某城有兩個出租車公司，分別是藍色和綠色公司。在所有出租車中 85%的出租車是藍色， 15%的是綠色。一輛出租車涉嫌一樁深夜肇事逃逸案。目擊者事後確認那輛車是綠色的。法庭測試了該目擊者在夜間視覺條件下辨別藍色和綠色出租車的能力，發現他在 80%的次數中能夠正確辨別各種顏色，但 20%的次數卻與另一顏色混淆。那麼你認為肇事車輛如目擊者所言是綠色的機率是多大呢？

用“機率樹+貝葉斯公式”計算如下：

人類在認識和判斷上，天生有一種直覺無法迴避的偏差：

忽略基礎機率。

以上題為例分析如下：

• 在此問題中，最重要的基礎機率是道路上藍色、綠色出租車的比例，這應該成為判斷的起始點——在所有證據（例如目擊者證詞）呈現之前的“先驗機率”。

•  Bar-Hillel（1980）發現，當她將此問題呈獻給不同群體的人時，人們普遍都忽視基礎機率；當人們聽到具體的目擊證詞時，基礎機率便黯然遁入背景之中。

• 於是，典型的答案是目擊者的正確率為 0.80，人們並未根據基礎機率資訊進行調整。

• 如果我們將這些數字代入貝葉斯定理的公式中（見上圖），我們可以得到正確答案： 0.41。

在此，我們的焦點不是討論人類直覺搞不掂基礎機率，而是對基礎機率的主觀設定，然後根據新的資訊進行調整。

3. 詭異的魔力

貝葉斯公式的詭異之處在於，有些時候，作為基礎機率的先驗機率，可能只是主觀猜測的，但仍然能夠對未來做出預測。

這有異於休謨和波普爾的“我極可能錯了”之懷疑和證偽。所以相當長一段時間，貝葉斯公式不被待見。

貝葉斯統計的優勢在於：

• 在資料少的情況下也可以進行推測，資料越多，推測結果越準確；

• 對所獲的資訊可做出瞬時反應，自動升級推測”的學習功能。

研究者發現：人們學習新的概念，往往能從單一的案例中學習，尤其是孩子。而機器學習則需要成千上萬的資料才能達到類似的精度。人們也可以用更豐富的方式學習概念，例如在行動、想象和解釋層面。

於是科學家們提出了一個計算模型，捕捉到人類的學習能力，為基於字母的手寫體創造出直觀的概念。在這模型背後，研究者使用了簡單的貝葉斯程式完成。在這個具有挑戰性的分類任務中，貝葉斯程式戰勝了深度學習方法，達到了人類的水平。這個模型也透過了圖靈測試。

一個簡單的數學概念為何會產生如此魔力？

研究人員提出以下討論：

• 人類大腦的思考和決策過程，是否如同貝葉斯程式一樣？

• 我們知道達爾文用極其簡單的模型解釋了人類複雜的進化行為，那麼貝葉斯定理會成為人類大腦的進化論嗎？

• 大腦認知是一種貝葉斯程式嗎？

4. 暈眩的四則運算

貝葉斯公式非常簡單，只需四則運算就能搞掂。在《統計學關我什麼事》一書中，作者用圖示法，讓我們能夠更直觀地進行貝葉斯計算。

問題：假設夫妻倆的第一個孩子是女兒。那麼，接下來生的孩子依然是女兒的機率為多少？

在我過往提及大數定律的文章裡，這道題的答案當然應該是50%。

然而，那是假設生男生女的機率各是50%。從醫學上看，有些夫妻的先天條件可能更加偏向於生男或者生女。

但我們這對夫妻的狀況一無所知。

貝葉斯推理的魅力正在於：即使沒有事前的客觀資料，也能進行推算。也就是說，可以主觀設定先驗機率，進行推算。

這可以更進一步解釋為：學會這個方法，才能更深刻地理解“貝葉斯推理的思想”，全面瞭解它的神奇和不可思議，以及奇怪和可疑之處。

第一步：猜一猜“機率的機率”。

即使我們也不知道這對夫妻的真實狀況，姑且猜一下，他們生女孩的可能性或者是40%，或者是50%，或者是60%。

由於我們對上面三種可能性只是猜猜，所以這三種可能性各自的機率都估為1/3。

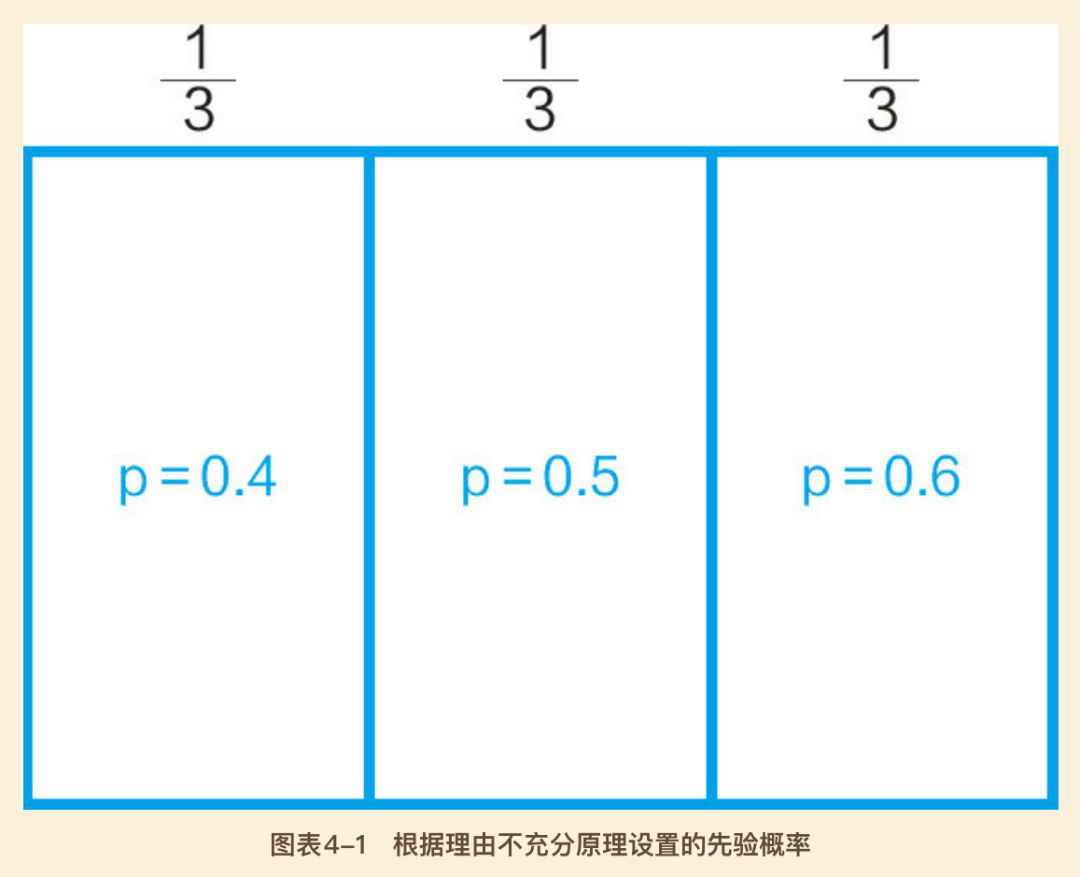
第二步：根據以上猜測的數字，開始計算三種可能性的情況下，生男孩女孩的機率。

第三步：把第二步的計算結果，裝到第一步的三個“預測盒”裡。

簡化如下：

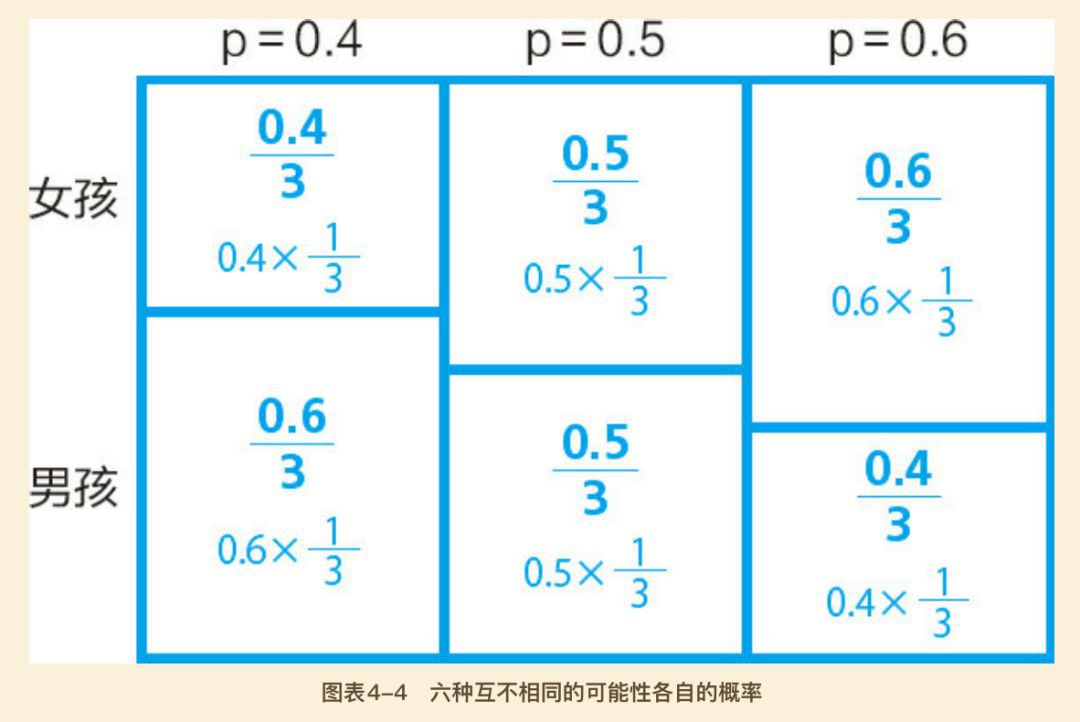
第四步：因為我們現在有“夫妻第一個孩子是女孩”的資訊，所以我們根據此資訊掃清一下。

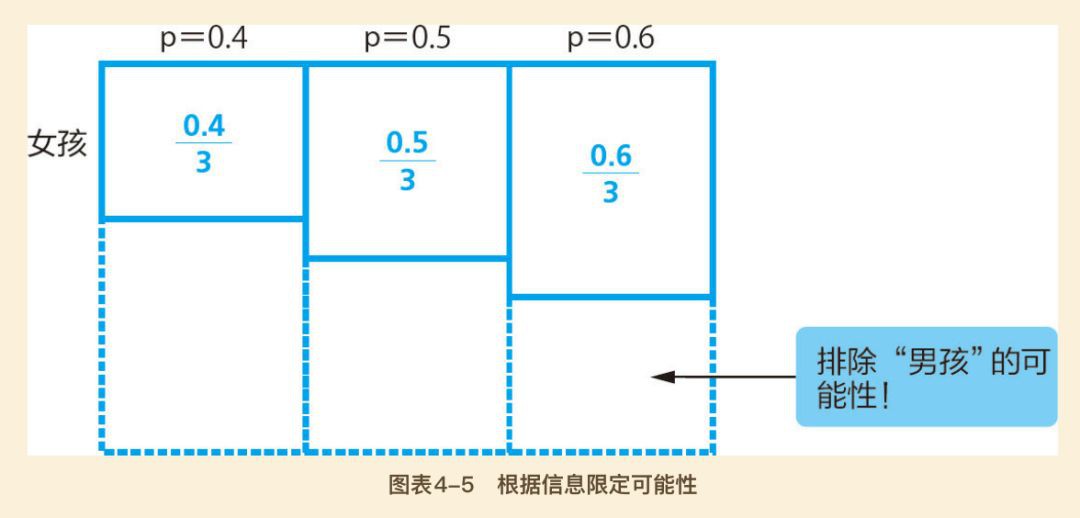
第五步：根據更新後的資訊，我們重新計算p（生女孩的可能性）分別為0.4、0.5、0.6三種情況下各自的機率。

如上圖，三者的比例是4:5:6，所以各自的更新後的機率，由原來毛估估的1/3，變為：4/15，5/15，6/15。

第六步：我們先毛估估，然後用第一個孩子是女孩的已有資訊掃清，得出了新的機率猜測。然後我們用此資料來計算第二胎生女孩的機率。

採用本文開始的期望值計算方法，或者用更直觀的決策樹計算：

x=0.4*0.27+0.5*0.33+0.6*0.4=0.513

所以，生第二個女孩的機率是51.3%。

5. 像人一樣

以上推理過程，如下圖：

《統計學關我什麼事》總結道：

主觀和客觀。我們在初中、高中階段學習的機率，是一個客觀的概念。也就是說，對於“某現象的機率是多少”的問題來說，答案是唯一的，無論是誰回答，都會給出一個唯一、客觀的數值。在“擲骰子出現 1的機率為六分之一”的情況下，機率表示的是：丟出這個骰子後，出現的結果為 1的可能性的程度。這個答案對於所有人來說，都是相同的。

然而，本講中提到的“機率”，並非上述的客觀性機率。“第二胎還是女孩的的機率”這一情況下的“機率”，並不能像上述擲骰子事件的機率那樣進行解釋。應當解釋為：你內心描繪的類似“信念程度”這樣的概念。也就是說，並非“機率是多少”的問題，而應該理解為“你認為機率是多少”。

像這樣，可以解釋為“人的內心描繪的數值”的機率稱為“主觀機率”。主觀機率在學校教育中並不涉及，因此，很多人會認為主觀機率是不可信的。但在統計學和經濟學中，“主觀機率”始終佔有一席之地。

總經理的機率。貝葉斯推理的強項是“無論在何種條件下，都能得出一個暫時的結果”。但是，這個結果並不像內曼－皮爾遜統計學那樣，得出一個單方面的判斷（非 A即 B），而是認為兩種可能性都有，並賦予這兩種可能性相應的比例關係，僅此而已。而“看到數值之後，做出判斷”的工作，就留給統計學家們了。因此，貝葉斯推理也常被稱為“總經理的機率”，它的含義是：貝葉斯推理就像是公司職員進行篩選和鑒別，最終由總經理根據下屬報告上來的數值進行判斷。

極大似然原理。世界上正在發生的事件，之所以發生，是因為它發生的機率大。

學習功能。貝葉斯推理中，修改過的“各個類別的後驗機率”，已經使用了所有的資訊。也就是說我們可以將其看作“從資訊中學習到的結果”。貝葉斯推理正是具備了“收集資訊並自動變聰明”的功能。

貝葉斯推理擁有“人類特性”的功能。我們總是對他人的能力和人性等進行評估。這時，我們並不是始終“調動迄今為止的記憶來進行評價”的，而是透過觀察這個人的某些行為，做出對其印象的判斷。一般情況下，這些行為事後就會被忘記了。在此基礎上形成的印象，經歷了下一次新的觀察之後，也會再一次被轉化為新的印象。

如果我們不斷地重覆“資訊” →“修改印象” →“遺忘資訊”的過程，慢慢地就會形成了對這個人的固定評價。

重要的是，像這樣透過逐步“修改印象”得出的結果，與“透過迄今為止的所有觀察，一次性形成的印象”之間，並沒有太大的偏差。

因此，我們沒有必要總是“從白紙開始思考”，這樣會耽誤大量的時間和精力。

貝葉斯推理，其實就像我們日常每天都在做的“印象的修改”和“學習”等一樣，只不過是運用了系統的數值來進行計算。

6. 簡單的真理

貝葉斯公式這類計算，能夠讓我們對某些簡單的大道理有更深刻的理解。只有洞察了背後的原理，真理才能被稱為真理，否則與雞湯無異。

如此，我們便能理解為什麼達利歐說：捲入快速學習的反饋迴圈之中是件令人興奮的事情。

我們也才算明白了“復盤、飛輪、掃清、升級”的價值與意義。

假如我們僅從時間的某個切片，二維地看貝葉斯公式，其實只是一個簡單的四則運算罷了。

但是，在時間的這個維度加入以後，切片與切片之間建立起聯絡，魔法出現了。

貝葉斯的神奇之處在於，你在主觀設定先驗機率時，並不需要那麼精確。

我與一些牛人接觸過程中發現，他們並不比別人更聰明，當他們接觸到新鮮事物時，經常因為天賦一般，而不能有領先一步的判斷，你甚至會懷疑這個傢伙如此普通，憑什麼擁有這麼多？

芒格曾在演講裡說：

不少人都能在晉級測試或快速計算中表現得極為機敏，但他們接二連三地犯愚蠢的錯誤，這僅僅因為腦海中層出不窮的瘋狂念頭。

尼采曾說過：“總會有人以自己擁有跛腳為榮。”如果你曾遭受失敗而不思悔改，將以自己的方式滑向淺薄。妒忌、太多的自我憐憫、偏激的思想、強烈的愚忠，所有這些作為一個明顯的標誌，表明你已經失去大腦並將被鐵鎚所痛擊。

進而，芒格分析了巴菲特的曠世成功之謎：

具有決定性的因素是沃倫是這個世界上最佳的持續學習機器。

烏龜最終戰勝兔子是持續努力的結果，一旦你停止了學習，整個世界將從你身旁呼嘯而過。

巴菲特這類人，擁有一個強大的貝葉斯大腦。

具有嘲諷意味的是，小孩子天生擁有鮮活的貝葉斯大腦，我們卻用刷題將他們變成機器。

7. 貝葉斯的未來

如前所述，科學哲學家卡爾·波普爾認為，一種理論必須是可證偽的才是科學的理論。

但有些科學理論無法證偽。如弦論，平行宇宙理論。

一群物理學家、哲學家和歷史學家，曾聚集在德國慕尼黑參加一個三天的科學哲學研討會。

基礎物理學正面臨一大難題。在場的科學哲學家指出：

• 波普爾派的可證偽性已經被貝葉斯的確定性理論所替代；

• 貝葉斯理論允許將理論建在從未直接觀察的現象，然後根據後續的資訊調整可信度。

• 貝葉斯理論的框架比波普爾理論更靈活。
  

在《終極演演算法》裡，作者分析了機器學習的五大學派，貝葉斯學派是其中之一：

貝葉斯學派最關註的問題是不確定性。

所有掌握的知識都有不確定性，而且學習知識的過程也是一種不確定的推理形式。

那麼問題就變成，在不破壞資訊的情況下，如何處理嘈雜、不完整甚至自相矛盾的資訊。

解決的辦法就是運用機率推理，而主演演算法就是貝葉斯定理及其衍生定理。

貝葉斯定理告訴我們，如何將新的證據併入我們的信仰中，而機率推理演演算法盡可能有效地做到這一點。

10 在無知的宇宙飛行

1. 精益創業=試錯+貝葉斯

隨著這個世界更加數字化、更加金融化，貝葉斯如魚得水。

這個時代的新常態，有四個關鍵詞：VUCA。

V是動蕩；U是不確定；C是複雜；A是模糊。

世界的執行規則，由拉普拉斯的“決定論”，變為不可測的“複雜論”。

龔焱教授分析了矽谷的創業樣式的演變。

矽谷傳統的創業樣式是“火箭發射式樣式”，即GBF樣式：

GET(獲取好創意)，BIG(大市場)，FAST(快速發展)。

但這需要天才人物的天才計劃，完美創意的完美執行。最失敗的是，在充分準備後按下火箭 按鈕，卻無聲無息。既沒有正面效應，也沒有負面反饋。

隨後，數字殖民地崛起，演演算法推動打了荷爾蒙的科學實驗，矽谷進入著名的“精益創業”時代。

精益創業=證偽+貝葉斯。

創業者快速試錯，多次迭代，一步步模擬接近真實客觀世界。

火箭發射樣式追求：可度量、可預測、確定性；

而精益創業樣式則是： 不可度量、 不可預測、不確定性。

其實孩子的成長也適用於“精益創業”樣式，可父母們總想按照火箭發射的樣式來設定孩子的未來。

精益創業有五項基本原則：1、使用者導向原則；2、行動原則；3、試錯原則；4、聚焦原則；5、迭代原則。

龔教授總結道：

商業設計提供關鍵的假設，使用者開發提供實驗的場景和通道，MVP提供資料，然後再把資料回到基本假設，精益創業是一個基於試驗的方法論。

一個初創公司本質上是一個學習機器，你的學習的速度，迭代的速度決定了你能跑多快，跑多遠。

貝葉斯定理的收斂性。讓出發點、認知完全不同的認知主體，透過不斷收集資訊和迭代，最後認知會趨同。

在實際應用中，精益創業可能的麻煩是：

1. 貝葉斯的問題在於，有些先驗和現實之間差別太大，導致了過高的方差以至於過擬合。輸入的太垃圾，輸出的還是垃圾。

2. 試錯性學習，有可能對短期的回報最大化，但是有可能讓你喪失重要的長期性回報。

3. 大方向還是要靠創始人的戰略定位。所以快速試錯首先應該是在某個半徑內進行的。

從亞馬遜和特斯拉等公司來看，既需要自上而下的願景，又需要自下而上的實踐，二者缺一不可，且不能彼此替代。

願景本身也是計算的一部分。很多時候是決定性的。

人和公司一樣，需要指北針。

所以，偉大的企業都有一個共同點：

他們都有一個崇高而熱切的標的。

Quirky的理想是“讓發明觸手可及”，奇點大學的理想是“為 10億人帶來積極的影響”。這個標的就是“宏大變革標的”（ MTP, Massive Transformative Purpose）。

《指數型組織》作者認為，足夠鼓舞人心的 MTP，本身就是一種競爭優勢，它會激勵人們創造出自身的社群、群體和文化。

這方面的極致，恐怕就是Space X的MTP了：

去火星，讓人類成為跨星球物種。

2. 上帝和科學

凱恩斯曾說：“牛頓不是理性時代的第一人，他是最後的一位煉金術士。”

那個時代煉金術與科學還沒有明確的區別。又或者，多年以後人們看我們如今也與煉金術無異？

但是，如果牛頓沒有依靠神秘學思想來解釋穿過真空的超距作用，他可能也不會發展出他的重力理論。

牛頓反對將宇宙解釋為一部純粹的機器，譬如一座大鐘。他說：“引力解釋了行星的運動，但卻不能解釋誰讓行星運動起來的。上帝統治萬物，知曉所有做過和能做的事。”

另一方面，牛頓是完整的物理因果關係創始人，因果關係正是經典物理學的基石。

作為與西方哲學和宗教的態度分歧，中國的宇宙學家們沒假設有某種不動的第一推動者透過自然法則來管轄宇宙，而是相信天體的行為與凡間的人類社會相關聯。這被視為中國沒有產生近代實驗科學的原因之一。

斯賓諾莎則把自然看成是上帝本身。對他來說，上帝在一切事物之內，是支配宇宙的物理和自然法則的系統本身。

愛因斯坦推崇斯賓諾莎，但他不認為自然是上帝，而是支配宇宙的完美法則的化身，人類是可以透過理性探索去瞭解其中一部分的。

而在霍金眼裡，宇宙中的所有結構都起源於量子力學的不確定性原理允許的最小起伏。

3. 信念

我更願意視休謨為“不可知論者”，而非徹底的“懷疑主義者”。

塔勒布認為休謨的一生基本上印證了他對自己的描述：“這是一個性情溫和，能夠自製，坦誠而友好，愉快而幽默，能夠依附但不會產生仇恨，各方面感情都十分適度的人。”

亞當·斯密在休謨的訃告結尾寫道：“總之，無論在休謨生前還是死後，我始終認為，他在人的天性弱點所允許的範圍內已經近乎一個全智全德之人。”

休謨是第一個認真考慮信念問題的哲學家。

對於信念的作用，休謨的基本看法是，信念強化了我們的有關觀念，使之變得更加強烈、生動，這有助於在因果的推論中，使我們能夠從原因的“印象”中，透過“相信”這一因果聯絡的存在，藉此推移到結果的“觀念”。

康德將確認我們“視其為真”的根據之充分性分為三個層次：“意見、信念和知識”。

• 意見屬於最低的層次，在主觀上、客觀上都不充分；

• 信念高於意見，在客觀上不充分，在主觀上充分；

• 知識屬於最高的層次，在主觀上和客觀上都充分。

康德把主觀上根據的充分性叫做“確信”，客觀上根據的充分性叫做“確定性”。

羅素視信念為“有機體的一種狀態”，是由“肌肉、感官和情緒，也許還有某些視覺意象所構成的某種狀態”，包括有身體上與心理上的兩方面表現。

英國哲學家萊姆賽的信念論兼有實用主義與行為主義的色彩。

首先，他把信念看作決定我們行動的力量；我們是否做出某種行動，取決於我們信念的力度。例如，在“火車要開動”這一信念與“到火車站趕火車”的行為之間，存在著一種可測度的聯絡。信念的力度越大，行動的欲求也相應越大；並且他還用“機率”來測度信念的力度。

其次，最有影響的，是他的“信念是我們藉以駕駛的鄰近空間的路線圖”的說法。

在這篇漫長的文章裡，從荒誕的科幻小說，到機率、演演算法、證偽、貝葉斯，信念貫穿其中。當我們為決策樹的分枝機率賦予數值，當我們在有限的資訊下為先驗機率“毛估估”，當我們穿行於創業維艱的夜晚，當我們在虛無的宇宙間飄浮，信念既是我們回應世界的方式，又決定了世界最終如何支配我們。

無論我們多麼無知，我們的信念多麼不靠譜，萬物之神都會賜予人類一些貝葉斯公式般的搖籃，令我們如宇宙裡的孩子般蹣跚向前。

11 最後

曾有人問我，怎麼看時間和機率是上帝的左右手？

我答：時間、機率、上帝，這三者我不確定是否真的存在，但皆令我迷戀。如果世界由時間和空間構成，機率決定了你某時出現在某地的可能性大小，又或者只是你在某時某地對這個世界的觀察、或錯覺。

如果一切皆演演算法，情感、美學、道德是否不過是一套公式？自由意志是否仍然存在？

我胡亂寫道：

1. 根據貝葉斯定律，信念給先驗機率賦值，令計算得以進行。意義、情感等等是信念賦值的結果，或者就是先驗機率；

2. 自由意志靠幻覺實現，靠自我懷疑強化，或只是“湧現”的結果；

3. 意義等是被不斷最佳化的“恆定變數”，既給人類“現在”的激勵，也維持“將來”的穩定。

我覺得人對自由意志的懷疑，是自由意志最有趣的地方之一。

《大河灣》裡寫道：“我隱約感到人活著就是為了變老的，為了完成生命的跨度，獲取人生閱歷。人活著是為了獲取人生閱歷；而閱歷在本質上是無形的。快樂和痛苦——首先是痛苦——都沒有什麼意義。感受痛苦和尋求快樂一樣，都沒有任何意義。”

我不贊成、也不欣賞奈保爾的這類“無意義”。關於“人”，我願意跟隨黑格爾說，人的本質是精神，而精神的本質是自由。宇宙的遼闊，與機率的不確定性，賦予了我們以自由，哪怕只是錯覺。

馬斯克用重型獵鷹火箭將特斯拉跑車送上太空，儀錶盤上寫著“Don’t Panic”，這是寫在《銀河系漫遊指南》電子書封面上的一句話，意思是“不要恐慌”。

《銀河系漫遊指南》嘗試用“虛無主義”來警示人類需正視自身的幼稚與渺小，不要過度執著於追尋永遠無法得出的答案。

然而卻激勵了一個男人執著於飛向火星。

我隱隱約約記得不知是誰說的一句話：這個世界以我們的叩問方式來展現祂的某一面。

由此，我們或能輕巧而簡短地回答一下——生命、宇宙以及任何事情的終極答案是什麼？

那就是：

你。