寒假向大四女神表白的成功率最高？貝葉斯演演算法助你科學撩妹

作者：雲時之間
原文連結：

https://www.jianshu.com/p/b413129e369d

經作者授權釋出

眾所周知生活中涉及到感情的事情是很複雜的，把所有可能影響的因素都考慮到幾乎是不可能的。為此我們先對現實進行簡化，並做出一些合理的假設，考慮比較簡單的一種情況。

為了將實際複雜的問題進行簡化，我們做出下麵幾條合理的假設：

1. 假設一個女生願意在一段時間中和一位男生開始一段感情，並且在這段時間中有N個男生追求這位女生。N個男生以不同的先後順序向女生表白，即在任一時刻不存在兩個或兩個以上的男生向這位女生表白的情況的發生，而且任何一種順序都是完全等機率的。

2. 面對錶白後的男生，女生只能做出接受和拒絕兩種選擇，不存在曖昧或者其它選擇。

3. 任一時刻，女生最多隻能和一位男生談戀愛，不存在腳踏多船的情況。

4. 已經被拒絕的男生不會再次追求這位女生。

基於上述假設，我們想要找到這樣一種策略，使得女生以最大的機率在第一次選擇接受的那個男生就是N。

先考慮最簡單的一種策略，如果一旦有男生向女生表白，女生就選擇接受。這種策略下顯然女生以1/N的機率找到自己的Mr. Right。當N比較大的時候，這個機率就很小了，顯然這種策略不是最優的。

基於上面這些假設和模型，我們提出這樣一種策略：對於最先表白的M個人，無論女生感覺如何都選擇拒絕；以後遇到男生向女生表白的情況，只要這個男生的編號比前面M個男生的編號都大，即這個男生比前面M個男生更適合女生，那麼女生選擇接受，否則選擇拒絕。

下麵以N=3為例說明：

三個男生追求女生，共有六種排列方式：

1 2 3

1 3 2

2 1 3

2 3 1

3 1 2

3 2 1

如果女生採用上述最簡單的策略，那麼只有最後兩種排列方式選擇到Mr. Right，機率為2/3!=1/3。

如果女生採用上面我們提出的策略，這裡我們取M=1，即無論第一個人是否優秀，女生都選擇拒絕。然後對於之後的追求者，只要他比第一個男生更適合女生就選擇接受，否則拒絕。基於這種策略，“1 3 2”、“2 1 3”、“2 3 1”這三種排列順序下女生都會在第一次做出接受的選擇時遇到“3”，這樣我們就把這種機率增大到3/3!=1/2。

現在我們的問題就歸結為，對於一般的N，什麼樣的M才會使這種機率達到最大值呢？（在這種模型中，前面M個男生就被稱為“炮灰”，無論他們有多麼優秀都要被拒絕）

01 模型建立

在這一部分中，根據上面的模型假設，我們先找到對於給定的M和N(1

1到N個數字進行排列共有N!種可能。當數字N出現在第P位置（M

1. N在第P位置

2. 從M+1到P-1位置的數字要比前M位置的最大數字要小

運用數學中排列組合的知識，不難知道符合上面兩個條件的排列共有

這樣對於給定的M和N，P可以從M+1到N變化，求和化簡後得到給定M和N共有

種序列符合要求。

由此得到女生選擇接受時遇到Mr. Right的機率為

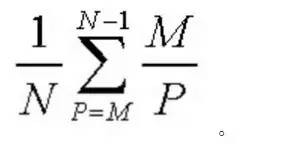
02 模型求解

（不感興趣的話可以直接跳過這部分推導）

這一部分中我們求解使這個運算式取得最大值時M的值。

記函式

且設自變數取值為M時，函式取得最大值。

因此：

所以M應滿足

我們知道，

當x>0, In(1+x)< x ;

當x–>0, In(1+x) ~ x。

所以由左不等式

所以：

當N比較大時，同理由右不等式可得M≈N/e，以上e為自然對數。

若記[x]為不大於x的最大整數，由以上推導我們可猜測當M取[N/e]或[N/e]+1時，該運算式取得最大值。

用MATLAB模擬，上述結論正確。

03 結果分析

由上述分析可以得到如下結論：為了使一個女生以最大的機率在第一次選擇接受男生時遇到的正是Mr. Right，女生應該採用以下的策略：

拒絕前M=[N/e]或者[N/e]+1個追求者，當其後的追求者比前M個追求者更適合則接受，否則拒絕。

現在到結婚的問題上：

現在給我們的問題是，如果一對男女朋友，男生向女生求婚，男生的四個特點分別是不帥，性格不好，身高矮，不上進，請你判斷一下女生是嫁還是不嫁？

這是一個典型的分類問題，轉為數學問題就是比較p(嫁|(不帥、性格不好、身高矮、不上進))與p(不嫁|(不帥、性格不好、身高矮、不上進))的機率，誰的機率大，我就能給出嫁或者不嫁的答案！

我們需要求p(嫁|(不帥、性格不好、身高矮、不上進)，這是我們不知道的，但是透過樸素貝葉斯公式可以轉化為好求的三個量。

p(不帥、性格不好、身高矮、不上進|嫁)、p(不帥、性格不好、身高矮、不上進)、p(嫁)

（至於為什麼能求，後面會講，那麼就太好了，將待求的量轉化為其它可求的值，這就相當於解決了我們的問題！）

那麼這三個量是如何求得？

是根據已知訓練資料統計得來，下麵詳細給出該例子的求解過程。

回憶一下我們要求的公式如下：

那麼我只要求得p(不帥、性格不好、身高矮、不上進|嫁)、p（不帥、性格不好、身高矮、不上進)、p(嫁)即可，好的，下麵我分別求出這幾個機率，最後一比，就得到最終結果。

p(不帥、性格不好、身高矮、不上進|嫁) = p(不帥|嫁)*p(性格不好|嫁)*p(身高矮|嫁)*p(不上進|嫁)，那麼我就要分別統計後面幾個機率，也就得到了左邊的機率！

等等，為什麼這個成立呢？學過機率論的同學可能有感覺了，這個等式成立的條件需要特徵之間相互獨立吧！

但是為什麼需要假設特徵之間相互獨立呢？

1. 我們這麼想，假如沒有這個假設，那麼我們對右邊這些機率的估計其實是不可做的，這麼說，我們這個例子有4個特徵，其中帥包括{帥，不帥}，性格包括{不好，好，爆好}，身高包括{高，矮，中}，上進包括{不上進，上進}，那麼四個特徵的聯合機率分佈總共是4維空間，總個數為2*3*3*2=36個。

36個，計算機掃描統計還可以，但是現實生活中，往往有非常多的特徵，每一個特徵的取值也是非常之多，那麼透過統計來估計後面機率的值，變得幾乎不可做，這也是為什麼需要假設特徵之間獨立的原因。

2. 假如我們沒有假設特徵之間相互獨立，那麼我們統計的時候，就需要在整個特徵空間中去找，比如統計p(不帥、性格不好、身高矮、不上進|嫁)，我們就需要在嫁的條件下，去找四種特徵全滿足分別是不帥，性格不好，身高矮，不上進的人的個數，這樣的話，由於資料的稀疏性，很容易統計到0的情況。 這樣是不合適的。

好的，上面我解釋了為什麼可以拆成分開連乘形式。那麼下麵我們就開始求解！

我們將上面公式整理一下如下：

下麵我將一個一個的進行統計計算（在資料量很大的時候，根據中心極限定理，頻率是等於機率的，這裡只是一個例子，所以我就進行統計即可）。

p(嫁)=？

首先我們整理訓練資料中，嫁的樣本數如下：

則p(嫁) = 6/12（總樣本數）= 1/2

p(不帥|嫁)=？統計滿足樣本數如下：

則p(不帥|嫁) = 3/6 = 1/2在嫁的條件下，看不帥有多少

p(性格不好|嫁)=？統計滿足樣本數如下：

則p(性格不好|嫁)= 1/6

p（矮|嫁）= ?統計滿足樣本數如下：

則p(矮|嫁) = 1/6

p(不上進|嫁) = ?統計滿足樣本數如下：

則p(不上進|嫁) = 1/6

下麵開始求分母，p(不帥)，p（性格不好），p（矮），p（不上進）

統計樣本如下：

不帥統計如上紅色所示，佔4個，那麼p（不帥）= 4/12 = 1/3

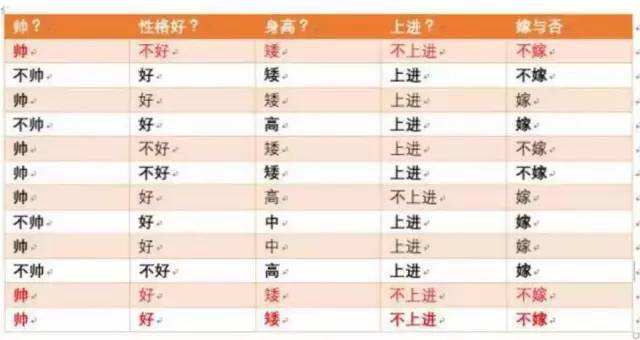
性格不好統計如上紅色所示，佔4個，那麼p（性格不好）= 4/12 = 1/3

身高矮統計如上紅色所示，佔7個，那麼p（身高矮）= 7/12

不上進統計如上紅色所示，佔4個，那麼p（不上進）= 4/12 = 1/3

到這裡，要求p(不帥、性格不好、身高矮、不上進|嫁)的所需項全部求出來了，下麵我帶入進去即可，

= (1/2*1/6*1/6*1/6*1/2)/(1/3*1/3*7/12*1/3)

下麵我們根據同樣的方法來求p(不嫁|不帥，性格不好，身高矮，不上進)，完全一樣的做法，為了方便理解，我這裡也走一遍幫助理解。首先公式如下：

下麵我也一個一個來進行統計計算，這裡與上面公式中，分母是一樣的，於是我們分母不需要重新統計計算！

p（不嫁）=？根據統計計算如下（紅色為滿足條件）：

則p(不嫁)=6/12 = 1/2

p(不帥|不嫁) =？統計滿足條件的樣本如下（紅色為滿足條件）：

則p（不帥|不嫁）= 1/6

p（性格不好|不嫁）=？據統計計算如下（紅色為滿足條件）：

則p（性格不好|不嫁）=3/6 = 1/2

p（矮|不嫁）=？據統計計算如下（紅色為滿足條件）：

則p（矮|不嫁）= 6/6 = 1

p（不上進|不嫁）=？據統計計算如下（紅色為滿足條件）：

則p（不上進|不嫁）= 3/6 = 1/2

那麼根據公式：

p (不嫁|不帥、性格不好、身高矮、不上進) = ((1/6*1/2*1*1/2)*1/2)/(1/3*1/3*7/12*1/3)

很顯然(1/6*1/2*1*1/2) > (1/2*1/6*1/6*1/6*1/2)

於是有p (不嫁|不帥、性格不好、身高矮、不上進)>p (嫁|不帥、性格不好、身高矮、不上進)

所以我們根據貝葉斯演演算法可以給這個女生答案，是不嫁！！！！

看完之後，我又簡單想了一下，在炮灰模型中，前M個男生就成了炮灰的角色，無論其有多麼優秀，都會被拒絕。

設女性最為燦爛的青春為18-28歲，在這段時間中將會遇到一生中幾乎全部的追求者（之前之後的忽略不計），且追求者均勻分佈，則女性從18+10/e=21.7即22歲左右開始接受追求……這告訴我們，想談戀愛找大四的……

在文章中只考慮了N個男生表白的先後順序是完全隨機的，並沒有考慮相鄰兩次之間的時間隔。如果把時間因素也考慮進去的話，在一個相對較短的時間中，可以近似的假設為齊次泊松過程，這樣不僅可以得出女生應該選擇上面的第M個男生的結論，而且找到男生表白的最佳時間在t=T/e時刻。 例如如果取時間段為大學四年的話，則T/e=1.4715。 也就是說，在大學四年裡，男生表白的最佳時刻在第三個學期的期末或寒假。

如果這個時間段較長的話，那麼男生追求可近似假設為了一個非齊次泊松過程，或者分段齊次泊松過程，具體建模中對各段引數lamma的估計就比較困難了，而且每個人以後的經歷都會不同，不太可能找到一個統一的引數集。

朋友，如果你追求一個女生而遭到拒絕，看完這篇文章後你會突然發現，也許這不是你的的錯，也許你真的很優秀，只是很不幸，你成了“炮灰”。

希望上面這些看似複雜的推導和模型對你能有所啟發。不要因為一次的拒絕而傷心、失落，振作起來！

例子來源於公眾號自然語言處理與機器學習貝葉斯部分例子一話