資料多到無法處理？微軟大牛用“分散式”搞定（附技術架構圖）-知識星球

導讀：近年來，作為人工智慧發展迅速的領域之一的深度學習在NLP、影象識別、語音識別、機器翻譯等方面都取得了驚人的成果。但是，深度學習的應用範圍卻日益受到資料量和模型規模的限制。如何才能高效地進行深度學習模型訓練？

微軟亞洲研究院機器學習組主管研究員陳薇和她的團隊基於對機器學習的完整理解，將分散式技術和深度學習緊密結合在一起，探索全新的真正合二為一“分散式深度學習”演演算法。

作者：陳薇

來源：微軟研究院AI頭條

隨著大資料和高效計算資源的出現，深度學習在人工智慧的很多領域中都取得了重大突破。然而，面對越來越複雜的任務，資料和深度學習模型的規模都變得日益龐大。例如，用來訓練影象分類器的有標簽的影象資料量達數百萬、甚至上千萬張。

大規模訓練資料的出現為訓練大模型提供了物質基礎，因此近年來湧現出了很多大規模的機器學習模型，例如2015年微軟亞洲研究院開發出的擁有超過兩百億個引數的LightLDA主題模型。

然而，當訓練資料詞表增大到成百上千萬時，如果不做任何剪枝處理，深度學習模型可能會擁有上百億、甚至是幾千億個引數。

為了提高深度學習模型的訓練效率，減少訓練時間，我們普遍會採用分散式技術來執行訓練任務——同時利用多個工作節點，分散式地、高效地訓練出效能優良的神經網路模型。分散式技術是深度學習技術的加速器，能夠顯著提高深度學習的訓練效率、進一步增大其應用範圍。

深度學習的標的是從資料中挖掘出規律，幫助我們進行預測。深度學習演演算法的一般框架是，利用最佳化演演算法迭代地最小化訓練資料上的經驗風險。

由於資料的統計性質、最佳化的收斂性質、以及學習的泛化性質在多機執行時的靈活度更高，相比於其它的計算任務，深度學習演演算法在並行化執行過程中實際上並不需要計算節點透過通訊嚴格地執行單機版本演演算法。

因而，當“分散式”遇到“深度學習”，不應只侷限在對序列演演算法進行多機實現以及底層實現方面的技術，我們更應該基於對機器學習的完整理解，將分散式和深度學習緊密結合在一起，結合深度學習的特點，設計全新的真正合二為一的“分散式深度學習”演演算法。

▲圖1 分散式深度學習框架

分散式深度學習框架中，包括資料/模型切分、本地單機最佳化演演算法訓練、通訊機制、和資料/模型聚合等模組。現有的演演算法一般採用隨機置亂切分的資料分配方式，隨機最佳化演演算法（例如隨機梯度法）的本地訓練演演算法，同步或者非同步通訊機制，以及引數平均的模型聚合方式。

結合深度學習演演算法的特點，微軟亞洲研究院機器學習組重新設計/理解了這些模組，我們在分散式深度學習領域主要做了三個方面的工作：

第一個工作，針對非同步機制中的梯度延遲問題，我們為深度學習設計了“帶有延遲補償的非同步演演算法”；
第二個工作，註意到神經網路的非凸性質，我們提出了比引數平均更加有效的整合聚合方式，並設計了“整合-壓縮”並行深度學習演演算法；
第三個工作，我們首次分析了隨機置亂切分方式下分散式深度學習演演算法的收斂速率，為演演算法設計提供了理論指導。

01 DC-ASGD演演算法：補償非同步通訊中梯度的延遲

隨機梯度下降法（SGD）是目前最流行的深度學習的最佳化演演算法之一，更新公式為：

▲公式 1

其中，w_t為當前模型，(x_t, y_t)為隨機抽取的資料，g(w_t; x_t, y_t)為(x_t, y_t)所對應的經驗損失函式關於當前模型w_t的梯度，η為步長/學習率。

假設系統中有多個工作節點並行地利用隨機梯度法最佳化神經網路模型，同步和非同步是兩種常用的通訊同步機制。

同步隨機梯度下降法（Synchronous SGD）在最佳化的每輪迭代中，會等待所有的計算節點完成梯度計算，然後將每個工作節點上計算的隨機梯度進行彙總、平均並按照公式1更新模型。之後，工作節點接收更新之後的模型，併進入下一輪迭代。

由於Sync SGD要等待所有的計算節點完成梯度計算，因此好比木桶效應，Sync SGD的計算速度會被運算效率最低的工作節點所拖累。

非同步隨機梯度下降法（Asynchronous SGD）在每輪迭代中，每個工作節點在計算出隨機梯度後直接更新到模型上，不再等待所有的計算節點完成梯度計算。因此，非同步隨機梯度下降法的迭代速度較快，也被廣泛應用到深度神經網路的訓練中。

然而，Async SGD雖然快，但是用以更新模型的梯度是有延遲的，會對演演算法的精度帶來影響。什麼是“延遲梯度”？我們來看下圖。

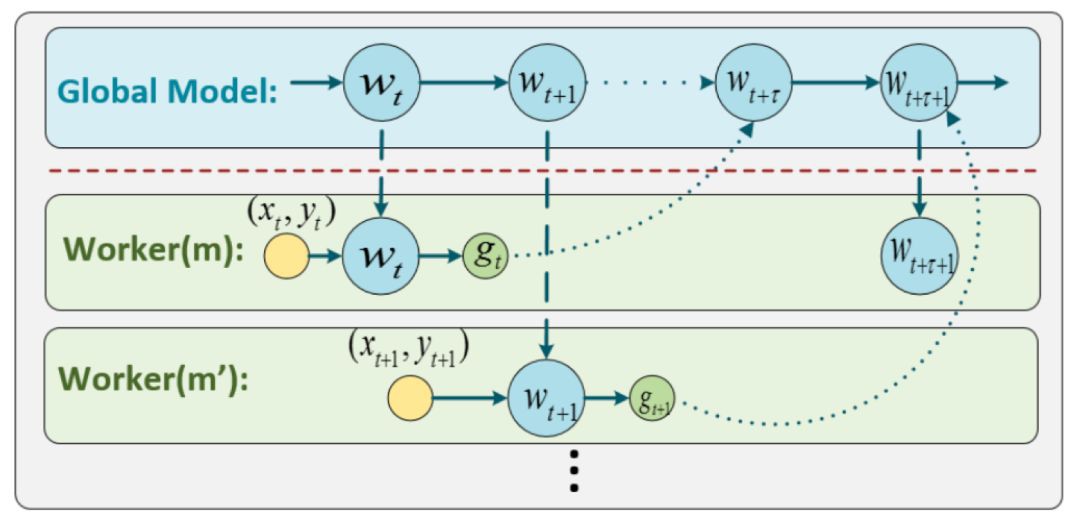
▲圖2 非同步隨機梯度下降法

在Async SGD執行過程中，某個工作節點Worker(m)在第t次迭代開始時獲取到模型的最新引數w_t和資料(x_t, y_t)，計算出相應的隨機梯度g_t，並將其傳回並更新到全域性模型w上。

由於計算梯度需要一定的時間，當這個工作節點傳回隨機梯度g_t時，模型w_t已經被其他工作節點更新了τ輪，變為了w_t+τ。也就是說，Async SGD的更新公式為：

▲公式 2

對比公式1，公式2中對模型w_t+τ上更新時所使用的隨機梯度是g(w_t; x_t, y_t)，相比SGD中應該使用的隨機梯度g(w_t+τ; x_t+τ, y_t+τ)產生了τ步的延遲。因而，我們稱Async SGD中隨機梯度為“延遲梯度”。

延遲梯度所帶來的最大問題是，由於每次用以更新模型的梯度並非是正確的梯度（請註意g(w_t; x_t, y_t) ≠ g(w_t+τ; x_t+τ, y_t+τ)），所以導致Async SGD會損傷模型的準確率，並且這種現象隨著機器數量的增加會越來越嚴重。如下圖所示，隨著計算節點數目的增加，Async SGD的精度逐漸變差。

▲圖3 非同步隨機梯度下降法的效能

那麼，如何能讓非同步隨機梯度下降法在保持訓練速度的同時，獲得更高的精度呢？我們設計了可以補償梯度延遲的DC-ASGD（Delay-compensated Async SGD）演演算法。

為了研究正確梯度g(w_t+τ)和延遲梯度g(w_t)之間的關係，我們將g(w_t+τ)在w_t處進行泰勒展開：

其中，∇g(w_t)為梯度的梯度，也就是損失函式的Hessian矩陣，H(g(w_t))為梯度的Hessian矩陣。顯然，延遲梯度實則為真實梯度的零階近似，而其餘各項造成了延遲。

於是，一個自然的想法是，如果我們將所有的高階項都計算出來，就可以修正延遲梯度為準確梯度了。然而，由於餘項擁有無窮項，所以無法被準確計算。因此，我們選擇用上述公式中的一階項進行延遲補償：

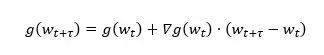
眾所周知，在現代的深度神經網路模型中有上百萬甚至更多的引數，計算和儲存Hessian矩陣∇g(w_t)成為了一件幾乎無法完成的事情。因此，尋找Hessian矩陣的一個良好近似是能否補償梯度延遲的關鍵。根據費舍爾資訊矩陣的定義，梯度的外積矩陣

是Hessian矩陣的一個漸近無偏估計，因此我們選擇用G(w_t)來近似估計Hessian矩陣。根據前人的研究，如果在神經網路模型中用Hessian矩陣的對角元來近似Hessian矩陣，在顯著降低運算和儲存複雜度的同事還可以保持演演算法精度，於是我們採用diag(G(w_t))作為Hessian矩陣的近似。

為了進一步降低近似的方差，我們使用一個(0,1]之間引數λ來對偏差和方差進行調節。綜上，我們設計瞭如下帶有延遲補償的非同步隨機梯度下降法（DC-ASGD），

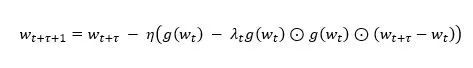
其中，對延遲梯度g(w_t)的補償項中只包含一階梯度資訊，幾乎不增加計算和儲存代價。

我們在CIFAR10資料集和ImageNet資料集上對DC-ASGD演演算法進行了評估，實驗結果見以下兩圖。

▲圖4 DC-ASGD的訓練/測試誤差_CIFAR-10

▲圖5 DC-ASGD的訓練/測試誤差_ImageNet

可以觀察到，DC-ASGD演演算法與Async SGD演演算法相比，在相同的時間內獲得的模型準確率有顯著的提升，並且也高於Sync SGD，基本可以達到SGD相同的模型準確率。

02 Ensemble-Compression演演算法：改進非凸模型的聚合方法

引數平均是現有的分散式深度學習演演算法中非常普遍的模型聚合方法。如果損失函式關於模型引數是凸的，以下不等式成立：

其中，K為計算節點個數，wk是區域性模型，為引數平均後的模型，(x, y)為任意樣本資料。該不等式的左端是平均模型所對應的損失函式，右端是各個區域性模型的損失函式值的平均值。可見，凸問題中引數平均可以保持模型的效能。

但是，對於非凸的神經網路模型，以上不等式將不再成立，因而平均模型的效能不再具有保證。這一點在實驗上也得到了驗證：如圖6所示，對於不同的互動頻率（尤其是較低頻的互動），引數平均通常會大幅度拉低訓練精度，使得訓練的過程極不穩定。

▲圖6 基於引數平均的分散式演演算法訓練曲線（DNN模型）

為瞭解決這個問題，我們提出用模型整合替代模型平均，作為分散式深度學習中的模型聚合方式。雖然神經網路的損失函式關於模型引數是非凸的，但是關於模型的輸出一般是凸的（比如深度學習中常用的交叉熵損失）。這時，利用凸性可以得到如下不等式：

其中，不等式左側是整合（ensemble）模型的損失函式取值。可見，對於非凸模型，整合模型可以保持效能。

然而，每經過一次整合，神經網路模型的規模就會增加倍，從而出現模型規模爆炸的問題。那麼，有沒有一種既能利用模型整合的優點，又能避免增大模型的方法呢？我們提出了一種同時基於模型整合和模型壓縮的模型聚合方法, 即整合-壓縮（ensemble-compression）方法。在每次整合之後，我們對整合所得的模型進行一次壓縮。

演演算法具體分為三個步驟：

各個計算節點依照本地最佳化演演算法訓練和區域性資料訓練出區域性模型；
計算節點之間相互通訊區域性模型得到整合模型，並對（一部分）區域性資料標註上整合模型對它們的輸出值；
利用模型壓縮技術（比如知識蒸餾），結合資料的再標註資訊，在每個工作節點上分別進行模型壓縮，獲得與區域性模型大小相同的新模型作為最終的聚合模型。為了進一步節省計算量，可以將蒸餾的過程和本地模型訓練的過程結合在一起。

這種整合-壓縮的聚合方法，既可以透過整合獲得效能提升，又可以在學習的迭代過程中保持全域性模型的規模。CIFA-10和ImageNet上的實驗結果也很好地驗證了整合-壓縮聚合方法的有效性（見圖7和圖8）。

當工作節點之間相互通訊的頻率較低時，引數平均方法表現會很差，但模型整合-壓縮的方法卻依然能取得理想的效果。這是因為整合學習在子模型具有多樣性時效果更好，而較低的通訊頻率會導致各個區域性模型更加分散，多樣性更強；同時，較低的通訊頻率意味著較低的通訊代價。

因此，模型整合-壓縮的方法更適用於網路環境比較差的場景。

▲圖7 CIFAR資料集上對比各種分散式演演算法

▲圖8 ImageNet資料集上對比各種分散式演演算法

基於模型整合的分散式演演算法是一個比較新的研究領域，還存在很多沒有解決的問題。比如說當工作節點非常多的時候或者本地模型本身就很大的時候，整合模型的規模會變得非常大，這會帶來較大的網路開銷。

另外，當整合模型較大時，模型壓縮也會變成一個較大的開銷。值得註意的是，在ICLR 2018上，Hinton等人提出的Co-distillation方法，儘管在動機上和這個工作不同，但是其演演算法和這個工作非常相似。如何理解這些關聯和解決這些侷限性將催生新的研究，感興趣的讀者可以對此進行思考。

03 隨機重排下演演算法的收斂性分析：改進分散式深度學習理論

最後，簡單介紹一個我們最近在改進分散式深度學習理論方面的工作。

分散式深度學習中常用的資料分配策略是隨機重排之後均等切分。具體來說，是將所有訓練資料隨機地打亂順序，得到資料的一個重排列，然後將資料集按順序等分，並將每一份存放在計算節點上。

在資料被過完一輪後，如果收集所有的區域性資料並重覆上述過程，一般被稱為“全域性重排”，如果只是對區域性資料進行隨機重排，一般被稱為“區域性重排”。

現有的絕大部分分散式深度學習理論中都假定資料是獨立同分佈的。然而，基於Fisher-Yates演演算法的隨機重排實際上與無放回抽樣等價，訓練資料之間不再是獨立同分佈的了。

於是，每一輪所計算的隨機梯度也不再是精確梯度的無偏估計，所以以往分散式隨機最佳化演演算法的理論分析方法不再適用，已有的收斂性結果也不一定仍然成立。

我們利用Transductive Rademancher Complexity作為工具，給出了隨機梯度相對於精確梯度的偏差上界，證明瞭隨機重排下分散式深度學習演演算法的收斂性分析。

假設標的函式光滑（不一定是凸函式），系統中有K個計算節點，訓練輪數(epoch)為S，總訓練資料有n個，考慮分散式SGD演演算法。

（1）如果採用全域性隨機重排資料分配策略，演演算法的收斂速率為，其中非i.i.d.性質帶來的額外誤差為。因此，當過資料的輪數遠遠小於訓練樣本數目時（S ≪n），額外誤差的影響可以忽略。考慮到現有的分散式深度學習任務中，S ≪n是很容易滿足的，所以全域性隨機重排不會影響分散式演演算法的收斂速率。

（2）如果採用區域性重排策略資料分配策略，演演算法的收斂速率為，其中非i.i.d.性質帶來的更大的額外誤差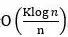。原因是，由於隨機重排是本地區域性進行的，不同計算節點之間的資料沒有進行互動，資料的差異性更大，隨機梯度的偏差也更大。

當過資料的輪數S≪n/K²時，額外誤差的影響可以忽略。也就是說，使用區域性重排資料分配策略時，演演算法中過資料的輪數要收到計算節點數目的影響。如果計算節點數比較多，過的輪數不能太大。

目前，分散式深度學習領域的發展非常迅速，而以上工作只是我們研究組所做的一些初步探索。希望本文能夠讓更多的研究人員瞭解“分散式”需要與“深度學習”進行深度融合，大家一起推動分散式深度學習的新發展！

參考文獻：

Shuxin Zheng, Qi Meng, Taifeng Wang, Wei Chen, Zhi-Ming Ma and Tie-Yan Liu, Asynchronous Stochastic Gradient Descent with Delay Compensation, ICML2017
Shizhao Sun, Wei Chen, Jiang Bian, Xiaoguang Liu and Tie-Yan Liu, Ensemble-Compression: A New Method for Parallel Training of Deep Neural Networks, ECML 2017
Qi Meng, Wei Chen, Yue Wang, Zhi-Ming Ma and Tie-Yan Liu, Convergence Analysis of Distributed Stochastic Gradient Descent with Shuffling, https://arxiv.org/abs/1709.10432

關於作者：