01 深度學習掀起海嘯

如今，深度學習浪潮拍打計算機語言的海岸已有好幾年，但是，2015年似乎才是這場海嘯全力衝擊自然語言處理（NLP）會議的一年。——Dr. Christopher D. Manning, Dec 2015

整個研究領域的成熟方法已經迅速被新發現超越，這句話聽起來有些誇大其詞，就像是說它被「海嘯」襲擊了一樣。但是，這種災難性的形容的確可以用來描述深度學習在過去幾年中的異軍突起——顯著改善人們對解決人工智慧最難問題方法的駕馭能力，吸引工業巨人（比如谷歌等）的大量投資，研究論文的指數式增長（以及機器學習的研究生生源上升）。在聽了數節機器學習課堂，甚至在本科研究中使用它以後，我不禁好奇：這個新的「深度學習」會不會是一個幻想，抑或上世紀80年代已經研發出來的「人工智慧神經網路」擴大版？讓我告訴你，說來話長——這不僅僅是一個有關神經網路的故事，也不僅僅是一個有關一系列研究突破的故事，這些突破讓深度學習變得比「大型神經網路」更加有趣，而是一個有關幾位不放棄的研究員如何熬過黑暗數十年，直至拯救神經網路，實現深度學習夢想的故事。

02 機器學習演演算法的百年曆史

線性回歸

首先簡單介紹一下機器學習是什麼。從二維影象上取一些點，盡可能繪出一條擬合這些點的直線。你剛才做的就是從幾對輸入值（x）和輸出值（y）的實體中概括出一個一般函式，任何輸入值都會有一個對應的輸出值。這叫做線性回歸，一個有著兩百年曆史從一些輸入輸出對組中推斷出一般函式的技巧。這就是它很棒的原因：很多函式難以給出明確的方程表達，但是，卻很容易在現實世界蒐集到輸入和輸出值實體——比如，將說出來的詞的音訊作為輸入，詞本身作為輸出的對映函式。

線性回歸對於解決語音識別這個問題來說有點太無用，但是，它所做的基本上就是監督式機器學習：給定訓練樣本，「學習」一個函式，每一個樣本資料就是需要學習的函式的輸入輸出資料（無監督學習，稍後在再敘）。尤其是，機器學習應該推匯出一個函式，它能夠很好地泛化到不在訓練集中的輸入值上，既然我們真的能將它運用到尚未有輸出的輸入中。例如，谷歌的語音識別技術由擁有大量訓練集的機器學習驅動，但是，它的訓練集也不可能大到包含你手機所有語音輸入。

泛化能力機制如此重要，以至於總會有一套測試資料組（更多的輸入值與輸出值樣本）這套資料組並不包括在訓練組當中。透過觀察有多少個正確計算出輸入值所對應的輸出值的樣本，這套單獨資料組可以用來估測機器學習技術有效性。概括化的剋星是過度擬合——學習一個對於訓練集有效但是卻在測試資料組中表現很差的函式。既然機器學習研究者們需要用來比較方法有效性的手段，隨著時間的推移，標準訓練資料組以及測試組可被用來評估機器學習演演算法。

好了，定義談得足夠多了。重點是——我們繪製線條的聯絡只是一個非常簡單的監督機器學習例子：要點在於訓練集（X為輸入，Y為輸出），線條是近似函式，用這條線來為任何沒有包含在訓練集資料裡的X值（輸入值）找到相應的Y值（輸出值）。別擔心，接下來的歷史就不會這麼乾巴巴了。讓我們繼續吧。

虛假承諾的荒唐

顯然這裡話題是神經網路，那我們前言裡為何要扯線性回歸呢？呃, 事實上線性回歸和機器學習一開始的方法構想,弗蘭克· 羅森布拉特(Frank Rosenblatt)的感知機, 有些許相似性。

Perceptron

心理學家Rosenblatt構想了感知機，它作為簡化的數學模型解釋大腦神經元如何工作：它取一組二進位制輸入值（附近的神經元），將每個輸入值乘以一個連續值權重（每個附近神經元的突觸強度），並設立一個閾值，如果這些加權輸入值的和超過這個閾值，就輸出1，否則輸出0（同理於神經元是否放電）。對於感知機，絕大多數輸入值不是一些資料，就是別的感知機的輸出值。但有一個額外的細節：這些感知機有一個特殊的，輸入值為1的，「偏置」輸入，因為我們能補償加權和，它基本上確保了更多的函式在同樣的輸入值下是可計算的。這一關於神經元的模型是建立在沃倫·麥卡洛克(Warren McCulloch)和沃爾特·皮茲(Walter Pitts)工作上的。他們曾表明，把二進位制輸入值加起來，併在和大於一個閾值時輸出1，否則輸出0的神經元模型，可以模擬基本的或/與/非邏輯函式。這在人工智慧的早期時代可不得了——當時的主流思想是,計算機能夠做正式的邏輯推理將本質上解決人工智慧問題。

另一個圖表，顯示出生物學上的靈感。啟用函式就是人們當前說的非線性函式，它作用於輸入值的加權和以產生人工神經元的輸出值——在羅森布拉特的感知機情況下，這個函式就是輸出一個閾值操作

然而，麥卡洛克-皮茲模型缺乏一個對AI而言至關重要的學習機制。這就是感知機更出色的地方所在——羅森布拉特受到唐納德·赫布(Donald Hebb) 基礎性工作的啟發，想出一個讓這種人工神經元學習的辦法。赫布提出了一個出人意料並影響深遠的想法，稱知識和學習發生在大腦主要是透過神經元間突觸的形成與變化，簡要表述為赫布法則：

當細胞A的軸突足以接近以激發細胞B，並反覆持續地對細胞B放電，一些生長過程或代謝變化將發生在某一個或這兩個細胞內，以致A作為對B放電的細胞中的一個，效率增加。

感知機並沒有完全遵循這個想法，但透過調輸入值的權重，可以有一個非常簡單直觀的學習方案：給定一個有輸入輸出實體的訓練集，感知機應該「學習」一個函式：對每個例子，若感知機的輸出值比實體低太多，則增加它的權重，否則若設比實體高太多，則減少它的權重。更正式一點兒的該演演算法如下:

1. 從感知機有隨機的權重和一個訓練集開始。

2. 對於訓練集中一個實體的輸入值，計算感知機的輸出值。

3. 如若感知機的輸出值和實體中預設正確的輸出值不同：(1)若輸出值應該為0但實際為1，減少輸入值是1的例子的權重。(2)若輸出值應該為1但實際為0，增加輸入值是1的例子的權重。

4. 對於訓練集中下一個例子做同樣的事，重覆步驟2-4直到感知機不再出錯。

這個過程很簡單，產生了一個簡單的結果：一個輸入線性函式（加權和），正如線性回歸被非線性啟用函式「壓扁」了一樣（對帶權重求和設定閾值的行為）。當函式的輸出值是一個有限集時（例如邏輯函式，它只有兩個輸出值True/1 和 False/0），給帶權重的和設定閾值是沒問題的，所以問題實際上不在於要對任何輸入資料集生成一個數值上連續的輸出（即回歸類問題），而在於對輸入資料做好合適的標簽（分類問題）。

康奈爾航天實驗室的Mark I 感知機，第一臺感知機的硬體 

羅森布拉特用定製硬體的方法實現了感知機的想法（在花哨的程式語言被廣泛使用之前），展示出它可以用來學習對20×20畫素輸入中的簡單形狀進行正確分類。自此，機器學習問世了——建造了一臺可以從已知的輸入輸出對中得出近似函式的計算機。在這個例子中，它只學習了一個小玩具般的函式，但是從中不難想象出有用的應用，例如將人類亂糟糟的手寫字轉換為機器可讀的文字。

很重要的是，這種方法還可以用在多個輸出值的函式中，或具有多個類別的分類任務。這對一臺感知機來說是不可能完成的，因為它只有一個輸出，但是，多輸出函式能用位於同一層的多個感知機來學習，每個感知機接收到同一個輸入，但分別負責函式的不同輸出。實際上，神經網路（準確的說應該是「人工神經網路（ANN，Artificial Neural Networks）」）就是多層感知機（今天感知機通常被稱為神經元）而已，只不過在這個階段，只有一層——輸出層。所以，神經網路的典型應用例子就是分辨手寫數字。輸入是影象的畫素，有10個輸出神經元，每一個分別對應著10個可能的數字。在這個案例中，10個神經元中，只有1個輸出1，權值最高的和被看做是正確的輸出，而其他的則輸出0。

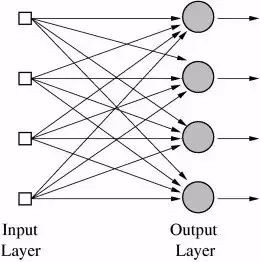
多層輸出的神經網路

也可以想象一個與感知機不同的人工神經網路。例如，閾值啟用函式並不是必要的； 1960年，Bernard Widrow和Tedd Hoff很快開始探索一種方法——採用適應性的「自適應（ADALINE）」神經元來輸出權值的輸入，這種神經元使用化學「 儲存電阻器」，並展示了這種「自適應線性神經元」能夠在電路中成為「 儲存電阻器」的一部分（儲存電阻器是帶有儲存的電阻）。他們還展示了，不用閾值啟用函式，在數學上很美，因為神經元的學習機制是基於將錯誤最小化的微積分，而微積分我們都很熟悉了。

如果我們多思考一下 「自適應（ADALINE）」，就會有進一步的洞見：為大量輸入找到一組權重真的只是一種線性回歸。再一次，就像用線性回歸一樣，這也不足以解決諸如語音識別或計算機視覺這樣的人工智慧難題。McCullough，Pitts和羅森布拉特真正感到興奮的是聯結主義（Connectionism）這個寬泛的想法：如此簡單計算機單元構成的網路，其功能會大很多而且可以解決人工智慧難題。而且羅森布拉特說的和（坦白說很可笑的）《紐約時報》這段引文的意思差不多：

海軍披露了一臺尚處初期的電子計算機，期待這臺電子計算機能行走，談話，看和寫，自己複製出自身存在意識…羅森布拉特博士，康奈爾航空實驗室的一位心理學家說，感知機能作為機械太空探險者被髮射到行星上。

這種談話無疑會惹惱人工領域的其他研究人員，其中有許多研究人員都在專註於這樣的研究方法，它們以帶有具體規則（這些規則遵循邏輯數學法則）的符號操作為基礎。MIT人工智慧實驗室創始人Marvin Minsky和Seymour Paper就是對這一炒作持懷疑態度研究人員中的兩位，1969年，他們在一本開創性著作中表達了這種質疑，書中嚴謹分析了感知機的侷限性，書名很貼切，叫《感知機》。

他們分析中，最被廣為討論的內容就是對感知機限制的說明，例如，他們不能學習簡單的布林函式XOR，因為它不能進行線性分離。雖然此處歷史模糊，但是，人們普遍認為這本書對人工智慧步入第一個冬天起到了推波助瀾的作用——大肆炒作之後，人工智慧進入泡沫幻滅期，相關資助和出版都遭凍結。

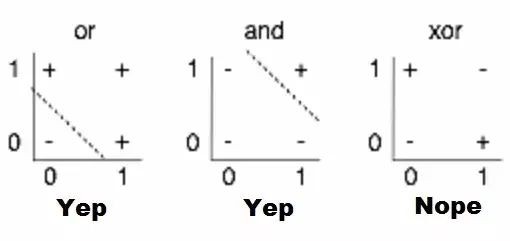
感知機侷限性的視覺化。找到一個線性函式，輸入X，Y時可以正確地輸出+或-，就是在2D圖表上畫一條從+中分離出-的線；很顯然，就第三幅圖顯示的情況來看，這是不可能的

人工智慧冬天的複蘇

因此，情況對神經網路不利。但是，為什麼？他們的想法畢竟是想將一連串簡單的數學神經元結合在一起，完成一些複雜任務，而不是使用單個神經元。換句話說，並不是隻有一個輸出層，將一個輸入任意傳輸到多個神經元（所謂的隱藏層，因為他們的輸出會作為另一隱藏層或神經元輸出層的輸入）。只有輸出層的輸出是「可見」的——亦即神經網路的答案——但是，所有依靠隱藏層完成的間接計算可以處理複雜得多的問題，這是單層結構望塵莫及的。 

有兩個隱藏層的神經網路 

言簡意賅地說，多個隱藏層是件好事，原因在於隱藏層可以找到資料內在特點，後續層可以在這些特點（而不是嘈雜龐大的原始資料）基礎上進行操作。以圖片中的面部識別這一非常常見的神經網路任務為例，第一個隱藏層可以獲得圖片的原始畫素值，以及線、圓和橢圓等資訊。接下來的層可以獲得這些線、圓和橢圓等的位置資訊，並且透過這些來定位人臉的位置——處理起來簡單多了！而且人們基本上也都明白這一點。事實上，直到最近，機器學習技術都沒有普遍直接用於原始資料輸入，比如影象和音訊。相反，機器學習被用於經過特徵提取後的資料——也就是說，為了讓學習更簡單，機器學習被用在預處理的資料上，一些更加有用的特徵，比如角度，形狀早已被從中提取出來。

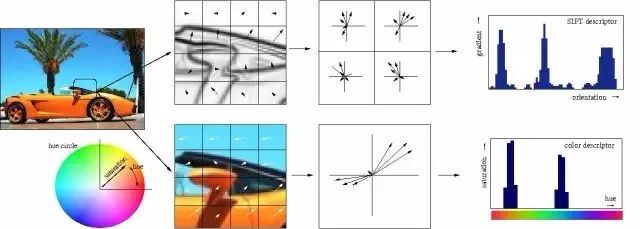
傳統的特徵的手工提取過程的視覺化

因此，註意到這一點很重要：Minsky和Paper關於感知機的分析不僅僅表明不可能用單個感知機來計算XOR，而且特別指出需要多層感知機——亦即現在所謂的多層神經網路——才可以完成這一任務，而且羅森布拉特的學習演演算法對多層並不管用。那是一個真正的問題：之前針對感知機概括出的簡單學習規則並不是適用於多層結構。想知道原因？讓我們再來回顧一下單層結構感知機如何學習計算一些函式：

1. 和函式輸出數量相等的感知機會以小的初始權值開始（僅為輸入函式的倍數）

2. 選取訓練集中的一個例子作為輸入，計算感知機的輸出

3. 對於每一個感知機，如果其計算結果和該例子的結果不匹配，調整初始權值

4. 繼續採用訓練集中的下一個例子，重覆過程2到4次，直到感知機不再犯錯。

這一規則並不適用多層結構的原因應該很直觀清楚了：選取訓練集中的例子進行訓練時，我們只能對最終的輸出層的輸出結果進行校正，但是，對於多層結構來說，我們該如何調整最終輸出層之前的層結構權值呢？答案（儘管需要花時間來推導）又一次需要依賴古老的微積分：鏈式法則。這裡有一個重要現實：神經網路的神經元和感知機並不完全相同，但是，可用一個啟用函式來計算輸出，該函式仍然是非線性的，但是可微分，和Adaline神經元一樣；該導數不僅可以用於調整權值，減少誤差，鏈式法則也可用於計算前一層所有神經元導數，因此，調整它們權重的方式也是可知的。說得更簡單些：我們可以利用微積分將一些導致輸出層任何訓練集誤差的原因分配給前一隱藏層的每個神經元，如果還有另外一層隱藏層，我們可以將這些原因再做分配，以此類推——我們在反向傳播這些誤差。而且，如果修改了神經網路（包括那些隱藏層）任一權重值，我們還可以找出誤差會有多大變化，透過最佳化技巧（時間長，典型的隨機梯度下降）找出最小化誤差的最佳權值。

反向傳播的基本思想 

反向傳播由上世紀60年代早期多位研究人員提出，70年代，由Seppo Linnainmaa引入電腦執行，但是，Paul Werbos在1974年的博士畢業論文中深刻分析了將之用於神經網路方面的可能性，成為美國第一位提出可以將其用於神經網路的研究人員。有趣的是，他從模擬人類思維的研究工作中並沒有獲得多少啟發，在這個案例中，弗洛伊德心理學理論啟發了他，正如他自己敘述：

1968年，我提出我們可以多少模仿弗洛伊德的概念——信度指派的反向流動（ a backwards flow of credit assignment,），指代從神經元到神經元的反向流動…我解釋過結合使用了直覺、實體和普通鏈式法則的反向計算，雖然它正是將弗洛伊德以前在心理動力學理論中提出的概念運用到數學領域中！

儘管解決瞭如何訓練多層神經網路的問題，在寫作自己的博士學位論文時也意識到了這一點，但是，Werbos沒有發表將BP演演算法用於神經網路這方面的研究，直到1982年人工智慧冬天引發了寒蟬效應。實際上，Werbos認為，這種研究進路對解決感知機問題是有意義的，但是，這個圈子大體已經失去解決那些問題的信念。

Minsky的書最著名的觀點有幾個：（1）我們需要用MLPs[多層感知機，多層神經網路的另一種說法）來代表簡單的非線性函式，比如XOR 對映；而且（2）世界上沒人發現可以將MLPs訓練得夠好，以至於可以學會這麼簡單的函式的方法。Minsky的書讓世上絕大多數人相信，神經網路是最糟糕的異端，死路一條。Widrow已經強調，這種壓垮早期『感知機』人工智慧學派的悲觀主義不應怪在Minsky的頭上。他只是總結了幾百位謹慎研究人員的經驗而已，他們嘗試找出訓練MLPs的辦法，卻徒勞無功。也曾有過希望，比如Rosenblatt所謂的backpropagation（這和我們現在說的 backpropagation並不完全相同！），而且Amari也簡短表示，我們應該考慮將最小二乘（也是簡單線性回歸的基礎）作為訓練神經網路的一種方式（但沒有討論如何求導，還警告說他對這個方法不抱太大期望）。但是，當時的悲觀主義開始變得致命。上世紀七十年代早期，我確實在MIT採訪過Minsky。我建議我們合著一篇文章，證明MLPs實際上能夠剋服早期出現的問題…但是，Minsky並無興趣（14）。事實上，當時的MIT，哈佛以及任何我能找到的研究機構，沒人對此有興趣。

我肯定不能打保票，但是，直到十年後，也就是1986年，這一研究進路才開始在David Rumelhart, Geoffrey Hinton和Ronald Williams合著的《Learning representations by back-propagating errors》中流行開來，原因似乎就是缺少學術興趣。

儘管研究方法的發現不計其數（論文甚至清楚提道，David Parker 和 Yann LeCun是事先發現這一研究進路的兩人），1986年的這篇文章卻因其精確清晰的觀點陳述而顯得很突出。實際上，學機器學習的人很容易發現自己論文中的描述與教科書和課堂上解釋概念方式本質上相同。

不幸的是，科學圈裡幾乎無人知道Werbo的研究。1982年，Parker重新發現了這個研究辦法[39]並於1985年在M.I.T[40]上發表了一篇相關報道。就在Parker報道後不久，Rumelhart, Hinton和Williams [41], [42]也重新發現了這個方法， 他們最終成功地讓這個方法家喻戶曉，也主要歸功於陳述觀點的框架非常清晰。

但是，這三位作者沒有止步於介紹新學習演演算法，而是走得更遠。同年，他們發表了更有深度的文章《Learning internal representations by error propagation》。

文章特別談到了Minsky在《感知機》中討論過的問題。儘管這是過去學者的構想，但是，正是這個1986年提出的構想讓人們廣泛理解了應該如何訓練多層神經網路解決複雜學習問題。而且神經網路也因此回來了！

神經網路獲得視覺

隨著訓練多層神經網路的謎題被揭開，這個話題再一次變得空前熱門，羅森布拉特的崇高雄心似乎也將得以實現。直到1989年另一個關鍵發現被公佈，現在仍廣為教科書及各大講座取用。

多層前饋神經網路是普適模擬器（ universal approximators）。」本質上，可以從數學證明多層結構使得神經網路能夠在理論上執行任何函式表達，當然包括XOR（異或）問題。

然而，這是數學，你可以在數學中暢想自己擁有無限記憶體和所需計算能力——反向傳播可以讓神經網路被用於世界任何角落嗎？噢，當然。也是在1989年，Yann LeCunn在AT&T; Bell實驗室驗證了一個反向傳播在現實世界中的傑出應用，即「反向傳播應用於手寫郵編識別（Backpropagation Applied to Handwritten Zip Code Recognition）」。

你或許會認為，讓計算機能夠正確理解手寫數字並沒有那麼了不起，而且今天看來，這還會顯得你太過大驚小怪，但事實上，在這個應用公開釋出之前，人類書寫混亂，筆畫也不連貫，對計算機整齊劃一的思維方式構成了巨大挑戰。這篇研究使用了美國郵政的大量資料資料，結果證明神經網路完全能夠勝任識別任務。更重要的是，這份研究首次強調了超越普通（plain）反向傳播 、邁向現代深度學習這一關鍵轉變的實踐需求。

傳統的視覺樣式識別工作已經證明，抽取區域性特徵並且將它們結合起來組成更高階的特徵是有優勢的。透過迫使隱藏單元結合區域性資訊來源，很容易將這樣的知識搭建成網路。一個事物的本質特徵可以出現在輸入圖片的不同位置。因此，擁有一套特徵探測器，可以探測到位於輸入環節任何地方的某個具體特徵實體，非常明智。既然一個特徵的精準定位於分類無關，那麼，我們可以在處理過程中適當捨棄一些位置資訊。不過，近似的位置資訊必須被保留，從而允許下麵網路層能夠探測到更加高階更加複雜的特徵。（Fukushima1980，Mozer,1987）

         一個神經網路工作原理的視覺化過程

或者，更具體的：神經網路的第一個隱層是摺積層——不同於傳統網路層，每個神經元對應的一個圖片畫素都相應有一個不同的權值（40*60=2400個權值），神經元只有很少一部分權值（5*5=25）以同樣的大小應用於影象的一小個完整子空間。所以，比如替換了用四種不同的神經元來學習整個輸入圖片4個角的45度對角線探測，一個單獨的神經元能透過在圖片的子空間上學習探測45度對角線，並且照著這樣的方法對整張圖片進行學習。每層的第一道程式都以相類似的方式進行，但是，接收的是在前一隱藏層找到的「區域性」特徵位置而不是圖片畫素值，而且，既然它們正在結合有關日益增大的圖片子集的資訊，那麼，它們也能「看到」其餘更大的圖片部分。最後，倒數的兩個網路層利用了前面摺積抽象出來的更加高階更加明顯的特徵來判斷輸入的影象究竟該歸類到哪裡。這個在1989年的論文裡提出的方法繼續成為舉國採用的支票讀取系統的基礎，正如LeCun在如下小影片中演示的：

這很管用，為什麼？原因很直觀，如果數學表述上不是那麼清楚的話：沒有這些約束條件，網路就必須學習同樣的簡單事情（比如，檢測45°角的直線和小圓圈等），要花大把時間學習影象的每一部分。但是，有些約束條件，每一個簡單特徵只需要一個神經元來學習——而且，由於整體權值大量減少，整個過程完成起來更快。而且，既然這些特徵的畫素確切位置無關緊要，那麼，基本上可以跳過影象相鄰子集——子集抽樣，一種共享池手段（a type of pooling）——當應用權值時，進一步減少了訓練時間。多加了這兩層——（摺積層和彙集層）——是摺積神經網路（CNNs/ConvNets）和普通舊神經網路的主要區別。

摺積神經網路（CNN）的操作過程

那時，摺積的思想被稱作「權值共享」，也在1986年Rumelhart、Hinton和Williams關於反向傳播的延伸分析中得到了切實討論。顯然，Minsky和Papert在1969年《感知機》中的分析完全可以提出激發這一研究想法的問題。但是，和之前一樣，其他人已經獨立地對其進行了研究——比如，Kunihiko Fukushima在1980年提出的 Neurocognitron。而且，和之前一樣，這一思想從大腦研究汲取了靈感：

根據Hubel和Wiesel的層級模型，視覺皮層中的神經網路具有一個層級結構：LGB（外側膝狀體）→樣品細胞→複雜細胞→低階超複雜細胞->高階超複雜細胞。低階超複雜細胞和高階超複雜細胞之間的神經網路具有一個和簡單細胞與複雜細胞之間的網路類似的結構。在這種層狀結構中，較高階別的細胞通常會有這樣的傾向，即對刺激樣式的更複雜的特徵進行選擇性響應，同時也具有一個更大的接收域，而且對刺激樣式位置的移動更不敏感。因此，在我們的模型中就引入了類似於層級模型的結構。

LeCun也在貝爾實驗室繼續支援摺積神經網路，其相應的研究成果也最終在上世紀90年代中期成功應用於支票讀取——他的談話和採訪通常都介紹了這一事實：「在上世紀90年代後期，這些系統當中的一個讀取了全美大約10%到20%的支票。」

神經網路進入無監督學習時期

將死記硬背，完全無趣的支票讀取工作自動化，就是機器學習大展拳腳的例子。也許有一個預測性小的應用？ 壓縮。即指找到一種更小體量的資料表示樣式，並從其可以恢復資料原有的表示形態，透過機器學習找到的壓縮方法有可能會超越所有現有的壓縮樣式。當然，意思是在一些資料中找到一個更小的資料表徵，原始資料可以從中加以重構。學會壓縮這一方案遠勝於常規壓縮演演算法，在這種情況下，學習演演算法可以找到在常規壓縮演演算法下可能錯失的資料特徵。而且，這也很容易做到——僅用訓練帶有一個小隱藏層的神經網路就可以對輸入進行輸出。

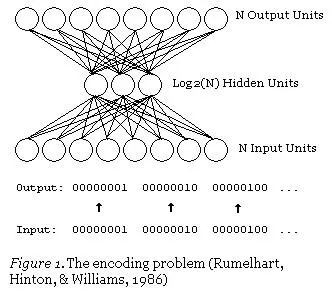
自編碼神經網路

這是一個自編碼神經網路，也是一種學習壓縮的方法——有效地將資料轉換為壓縮格式，並且自動傳回到本身。我們可以看到，輸出層會計算其輸出結果。由於隱藏層的輸出比輸入層少，因此，隱藏層的輸出是輸入資料的一個壓縮表達，可以在輸出層進行重建。

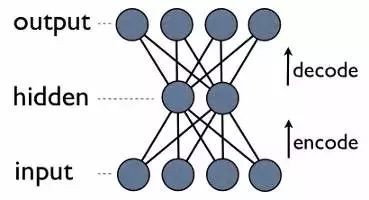
更明確地瞭解自編碼壓縮

註意一件奇妙的事情：我們訓練所需的唯一東西就是一些輸入資料。這與監督式機器學習的要求形成鮮明的對比，監督式機器學習需要的訓練集是輸入-輸出對（標記資料），來近似地生成能從這些輸入得到對應輸出的函式。確實，自編碼器並不是一種監督式學習；它們實際上是一種非監督式學習，只需要一組輸入資料（未標記的資料），目的是找到這些資料中某些隱藏的結構。換句話說，非監督式學習對函式的近似程度不如它從輸入資料中生成另一個有用的表徵那麼多。這樣一來，這個表徵比原始資料能重構的表徵更小，但它也能被用來尋找相似的資料組（聚類）或者潛在變數的其他推論（某些從資料看來已知存在但數值未知的方面）。

聚類，一種很常用的非監督式學習應用

在反向傳播演演算法發現之前和之後，神經網路都還有其他的非監督式應用，最著名的是自組織對映神經網路（SOM，Self Organizing Maps）和自適應共振理論（ART，Adapative Resonance Theory）。SOM能生成低維度的資料表徵，便於視覺化，而ART能夠在不被告知正確分類的情況下，學習對任意輸入資料進行分類。如果你想一想就會發現，從未標記資料中能學到很多東西是符合直覺的。假設你有一個資料集，其中有一堆手寫數字的資料集，並沒有標記每張圖片對應著哪個數字。那麼，如果一張圖片上有資料集中的某個數字，那它看起來與其他大多數擁有同樣數字的圖片很相似，所以，儘管計算機可能並不知道這些圖片對應著哪個數字，但它應該能夠發現它們都對應著同一個數字。這樣，樣式識別就是大多數機器學習要解決的任務，也有可能是人腦強大能力的基礎。但是，讓我們不要偏離我們的深度學習之旅，回到自編碼器上。

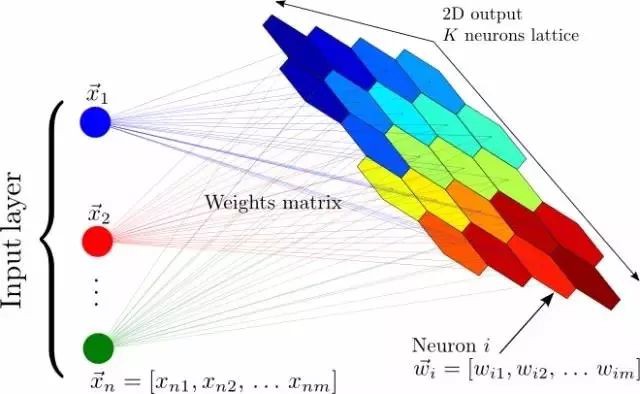
自組織對映神經網路：將輸入的一個大向量對映到一個神經輸出的網格中，在其中，每個輸出都是一個聚類。相鄰的神經元表示同樣的聚類。

正如權重共享一樣，關於自編碼器最早的討論是在前面提到過的1986年的反向傳播分析中所進行。有了權重共享，它在接下來幾年中的更多研究中重新浮出了水面，包括Hinton自己。這篇論文，有一個有趣的標題：《自編碼器，最小描述長度和亥姆霍茲自由能》（Autoencoders, Minimum Description Length, and Helmholts Free Energy），提出「最自然的非監督式學習方法就是使用一個定義機率分佈而不是可觀測向量的模型」，並使用一個神經網路來學習這種模型。所以，還有一件你能用神經網路來做的奇妙事：對機率分佈進行近似。

神經網路迎來信念網路

事實上，在成為1986年討論反向傳播學習演演算法這篇有重大影響力論文的合作者之前，Hinton在研究一種神經網路方法，可以學習1985年「 A Learning Algorithm for Boltzmann Machines」中的機率分佈。

玻爾茲曼機器就是類似神經網路的網路，並有著和感知器（Perceptrons）非常相似的單元，但該機器並不是根據輸入和權重來計算輸出，在給定相連單元值和權重的情況下，網路中的每個單元都能計算出自身機率，取得值為1或0。因此，這些單元都是隨機的——它們依循的是機率分佈而非一種已知的決定性方式。玻爾茲曼部分和機率分佈有關，它需要考慮系統中粒子的狀態，這些狀態本身基於粒子的能量和系統本身的熱力學溫度。這一分佈不僅決定了玻爾茲曼機器的數學方法，也決定了其推理方法——網路中的單元本身擁有能量和狀況，學習是由最小化系統能量和熱力學直接刺激完成的。雖然不太直觀，但這種基於能量的推理演繹實際上恰是一種基於能量的模型實體，並能夠適用於基於能量的學習理論框架，而很多學習演演算法都能用這樣的框架進行表述。

一個簡單的信念，或者說貝葉斯網路——玻爾茲曼機器基本上就是如此，但有著非直接/對稱聯絡和可訓練式權重，能夠學習特定樣式下的機率。

回到玻爾茲曼機器。當這樣的單元一起置於網路中，就形成了一張圖表，而資料圖形模型也是如此。本質上，它們能夠做到一些非常類似普通神經網路的事：某些隱藏單元在給定某些代表可見變數的可見單元的已知值（輸入——影象畫素，文字字元等）後，計算某些隱藏變數的機率（輸出——資料分類或資料特徵）。以給數字影象分類為例，隱藏變數就是實際的數字值，可見變數是影象的畫素；給定數字影象「1」作為輸入，可見單元的值就可知，隱藏單元給影象代表「1」的機率進行建模，而這應該會有較高的輸出機率。

玻爾茲曼機器實體。每一行都有相關的權重，就像神經網路一樣。註意，這裡沒有分層——所有事都可能跟所有事相關聯。我們會在後文討論這樣一種變異的神經網路

因此，對於分類任務，現在有一種計算每種類別機率的好方法了。這非常類似正常分類神經網路實際計算輸出的過程，但這些網路有另一個小花招：它們能夠得出看似合理的輸入資料。這是從相關的機率等式中得來的——網路不只是會學習計算已知可見變數值時的隱藏變數值機率，還能夠由已知隱藏變數值反推可見變數值機率。所以，如果我們想得出一幅「1」數字影象，這些跟畫素變數相關的單元就知道需要輸出機率1，而影象就能夠根據機率得出——這些網路會再建立影象模型。雖然可能能夠實現標的非常類似普通神經網路的監督式學習，但學習一個好的生成模型的非監督式學習任務——機率性地學習某些資料的隱藏結構——是這些網路普遍所需要的。這些大部分都不是小說，學習演演算法確實存在，而使其成為可能的特殊公式，正如其論文字身所描述的：

或許，玻爾茲曼機器公式最有趣的方面在於它能夠引匯出一種（與領域無關的）一般性學習演演算法，這種演演算法會以整個網路發展出的一種內部模型（這個模型能夠捕獲其周圍環境的基礎結構）的方式修改單元之間的聯絡強度。在尋找這樣一個演演算法的路上，有一段長時間失敗的歷史（Newell，1982），而很多人（特別是人工智慧領域的人）現在相信不存在這樣的演演算法。

我們就不展開演演算法的全部細節了，就列出一些亮點：這是最大似然演演算法的變體，這簡單意味著它追求與已知正確值匹配的網路可見單元值（visible unit values）機率的最大化。同時計算每個單元的實際最有可能值 ，計算要求太高，因此，訓練吉布斯取樣（training Gibbs Sampling）——以隨機的單元值網路作為開始，在給定單元連線值的情況下，不斷迭代重新給單元賦值——被用來給出一些實際已知值。當使用訓練集學習時，設定可見單位值（ visible units）從而能夠得到當前訓練樣本的值，這樣就透過抽樣得到了隱藏單位值。一旦抽取到了一些真實值，我們就可以採取類似反向傳播的辦法——針對每個權重值求偏導數，然後估算出如何調整權重來增加整個網路做出正確預測的機率。

和神經網路一樣，演演算法既可以在監督（知道隱藏單元值）也可以在無監督方式下完成。儘管這一演演算法被證明有效（尤其是在面對自編碼神經網路解決的「編碼」問題時），但很快就看出不是特別有效。Redford M. Neal1992年的論文《Connectionist learning of belief networks》論證了需要一種更快的方法，他說：「這些能力使得玻耳茲曼機在許多應用中都非常有吸引力——要不是學習過程通常被認為是慢的要命。」因此，Neal引入了類似信念網路的想法，本質上就像玻耳茲曼機控制、傳送連線（所以又有了層次，就像我們之前看過的神經網路一樣，而不像上面的玻耳茲曼機控制機概念）。跳出了討厭的機率數學，這一變化使得網路能以一種更快的學習演演算法得到訓練。灑水器和雨水那一層上面可以視為有一個信念網路——這一術語非常嚴謹，因為這種基於機率的模型，除了和機器學習領域有著聯絡，和數學中的機率領域也有著密切的關聯。

儘管這種方法比玻爾茲曼機進步，但還是太慢了，正確計算變數間的機率關係的數學需求計算量太大了，而且還沒啥簡化技巧。Hinton、Neal和其他兩位合作者很快在1995年的論文《 The wake-sleep algorithm for unsupervised neural networks》中提出了一些新技巧。這次他們又搞出一個和上個信念網路有些不一樣的網路，現在被叫做「亥姆霍茲機」。再次拋開細節不談，核心的想法就是對隱含變數的估算和對已知變數的逆轉生成計算採取兩套不同的權重，前者叫做recognition weights，後者叫做generative weights，保留了Neal’s信念網路的有方向的特性。這樣一來，當用於玻爾茲曼機的那些監督和無監督學習問題時，訓練就快得多。

最終，信念網路的訓練多少會快些！儘管沒那麼大的影響力，對信念網路的無監督學習而言，這一演演算法改進是非常重要的進步，堪比十年前反向傳播的突破。不過，目前為止，新的機器學習方法也開始湧現，人們也與開始質疑神經網路，因為大部分的想法似乎基於直覺，而且因為計算機仍舊很難滿足它們的計算需求，人工智慧寒冬將在幾年內到來。

神經網路做決定

神經網路運用於無監督學習的發現之旅結束後，讓我們也快速瞭解一下它們如何被用於機器學習的第三個分支領域：強化學習。正規解釋強化學習需要很多數學符號，不過，它也有一個很容易加以非正式描述的標的：學會做出好決定。給定一些理論代理（比如，一個小軟體），讓代理能夠根據當前狀態做出行動，每個採取行動會獲得一些獎勵，而且每個行動也意圖最大化長期效用。

因此，儘管監督學習確切告訴了學習演演算法它應該學習的用以輸出的內容，但是，強化學習會過一段時間提供獎勵，作為一個好決定的副產品，不會直接告訴演演算法應該選擇的正確決定。從一開始，這就是一個非常抽象的決策模型——數目有限的狀態，並且有一組已知的行動，每種狀態下的獎勵也是已知的。為了找到一組最優行動，編寫出非常優雅的方程會因此變得簡單，不過這很難用於解決真實問題——那些狀態持續或者很難界定獎勵的問題。

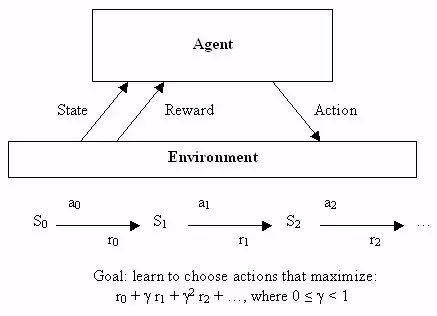
強化學習

這就是神經網路流行起來的地方。機器學習大體上，特別是神經網路，很善於處理混亂的連續性資料 ，或者透過實體學習很難加以定義的函式。儘管分類是神經網路的飯碗，但是，神經網路足夠普適（general），能用來解決許多型別的問題——比如，Bernard Widrow和Ted Hoff的Adaline後續衍生技術被用於電路環境下的自適應濾波器。

因此，BP研究複蘇之後，不久，人們就設計了利用神經網路進行強化學習的辦法。早期例子之一就是解決一個簡單卻經典的問題：平衡運動著的平臺上的棍子，各地控制課堂上學生熟知的倒立擺控制問題。

雙擺控制問題——單擺問題進階版本，是一個經典的控制和強化學習任務

因為有自適應濾波，這項研究就和電子工程領域密切相關，這一領域中，在神經網路出現之前的幾十年當中，控制論已經成為一個主要的子領域。雖然該領域已經設計了很多透過直接分析解決問題的辦法，也有一種透過學習解決更加複雜狀態的辦法，事實證明這一辦法有用——1990年，「Identification and control of dynamical systems using neural networks」的7000次高被引就是證明。或許可以斷定，另有一個獨立於機器學習領域，其中，神經網路就是有用的機器人學。用於機器人學的早期神經網路例子之一就是來自CMU的NavLab，1989年的「Alvinn: An autonomous land vehicle in a neural network」：

1. “NavLab 1984 – 1994”

正如論文所討論的，這一系統中的神經網路透過普通的監督學習學會使用感測器以及人類駕駛時記錄下的駕駛資料來控制車輛。也有研究教會機器人專門使用強化學習，正如1993年博士論文「Reinforcement learning for robots using neural networks」所示例的。論文表明，機器人能學會一些動作，比如，沿著牆壁行走，或者在合理時間範圍內透過門，考慮到之前倒立擺工作所需的長得不切實際的訓練時間，這真是件好事。

這些發生在其他領域中的運用當然很酷，但是，當然多數強化學習和神經網路的研究發生在人工智慧和機器學習範圍內。而且，我們也在這一範圍內取得了強化學習史上最重要的成績之一：一個學習併成為西洋雙陸棋世界級玩家的神經網路。研究人員用標準強化學習演演算法來訓練這個被稱為TD-Gammon的神經網路，它也是第一個證明強化學習能夠在相對複雜任務中勝過人類的證據。而且，這是個特別的加強學習辦法，同樣的僅採用神經網路（沒有加強學習）的系統，表現沒這麼好。

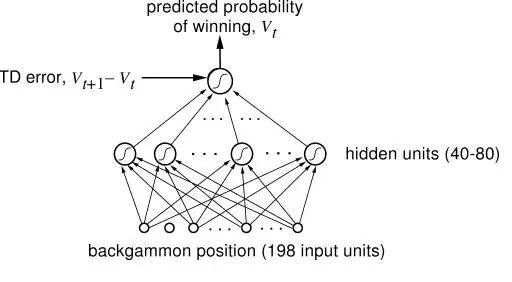
西洋雙陸棋遊戲中，掌握專家級別水平的神經網路

但是，正如之前已經看到，接下來也會在人工智慧領域再次看到，研究進入死衚衕。下一個要用TD-Gammnon辦法解決的問題，Sebastian Thrun已經在1995年「Learning To Play the Game of Chess」中研究過了，結果不是很好..儘管神經網路表現不俗，肯定比一個初學者要好，但和很久以前實現的標準計算機程式GNU-Chess相比，要遜色得多。人工智慧長期面臨的另一個挑戰——圍棋，亦是如此。這樣說吧，TD-Gammon 有點作弊了——它學會了精確評估位置，因此，無需對接下來的好多步做任何搜尋，只用選擇可以佔據下一個最有利位置的招數。但是，在象棋遊戲和圍棋遊戲裡，這些遊戲對人工智慧而言是一個挑戰，因為需要預估很多步，可能的行動組合如此之巨。而且，就算演演算法更聰明，當時的硬體又跟不上，Thrun稱「NeuroChess不怎麼樣，因為它把大部分時間花在評估棋盤上了。計算大型神經網路函式耗時是評價最佳化線性評估函式（an optimized linear evaluation function），比如GNU-Chess，的兩倍。」當時，計算機相對於神經網路需求的不足是一個很現實的問題，而且正如我們將要看到的，這不是唯一一個…

神經網路變得獃頭獃腦

儘管無監督學習和加強學習很簡潔，監督學習仍然是我最喜歡的神經網路應用實體。誠然，學習資料的機率模型很酷，但是，透過反向傳播解決實際問題更容易讓人興奮。我們已經看到了Yann Lecun成功解決了識別手寫的問題（這一技術繼續被全國用來掃描支票，而且後來的使用更多），另一項顯而易見且相當重要的任務也在同時進行著：理解人類的語音。

和識別手寫一樣，理解人類的語音很難，同一個詞根據表達的不同，意思也有很多變化。不過，還有額外的挑戰：長序列的輸入。你看，如果是圖片，你就可以把字母從圖片中切出來，然後，神經網路就能告訴你這個字母是啥，輸入-輸出樣式。但語言就沒那麼容易了，把語音拆成字母完全不切實際，就算想要找出語音中的單詞也沒那麼容易。而且你想啊，聽到語境中的單詞相比單個單詞，要好理解一點吧！儘管輸入-輸出樣式用來逐個處理圖片相當有效，這並不適用於很長的資訊，比如音訊或文字。神經網路沒有記憶賴以處理一個輸入能影響後續的另一個輸入的情況，但這恰恰是我們人類處理音訊或者文字的方式——輸入一串單詞或者聲音，而不是單獨輸入。要點是：要解決理解語音的問題，研究人員試圖修改神經網路來處理一系列輸入（就像語音中的那樣）而不是批次輸入（像圖片中那樣）。

Alexander Waibel等人（還有Hinton）提出的解決方法之一，在1989年的「 Phoneme recognition using time-delay neural networks」中得到了介紹。這些時延神經網路和通常意義上的神經網路非常類似，除了每個神經元只處理一個輸入子集，而且為不同型別的輸入資料延遲配備了幾套權重。易言之，針對一系列音訊輸入，一個音訊的「移動視窗」被輸入到神經網路，而且隨著視窗移動，每個帶有幾套不同權重的神經元就會根據這段音訊在視窗中位置，賦予相應的權重，用這種方法來處理音訊。畫張圖就好理解了：

時延神經網路

從某種意義上來說，這和摺積神經網路差不多——每個單元一次只看一個輸入子集，對每個小子集進行相同的運算，而不是一次性計算整個集合。不同之處在於，在摺積神經網路中不存在時間概念， 每個神經元的輸入窗形成整個輸入影象來計算出一個結果，而時延神經網路中有一系列的輸入和輸出。一個有趣的事實：據Hinton說，時延神經網路的理念啟發了LeCun開發摺積神經網路。但是，好笑的是，積捲神經網路變得對影象處理至關重要，而在語音識別方面，時延神經網路則敗北於另一種方法——遞迴神經網路(RNNs)。你看，目前為止討論過的所有神經網路都是前歸網路，這意味著某神經元的輸出是下一層神經元的輸入。但並不一定要這樣，沒有什麼阻止我們勇敢的電腦科學家將最後一層的輸出變成第一層的輸入，或者將神經元的輸出連線到神經元自身。將神經元迴路接回神經網路，賦予神經網路記憶就被優雅地解決了。

遞迴神經網路圖

還記得之前的玻爾茲曼機嗎？大吃一驚吧！那些是遞迴性神經網路。

然而，這可沒有那麼容易。註意這個問題——如果反向傳播需要依賴『正向傳播』將輸出層的錯誤反饋回來，那麼，如果第一層往回連線到輸出層，系統怎麼工作？錯誤會繼續傳到第一層再傳回到輸出層，在神經網路中迴圈往複，無限次地。解決辦法是，透過多重群組獨立推導，透過時間進行反向傳播。基本來說，就是將每個透過神經網路的迴路做為另一個神經網路的輸入，而且迴路次數有限，透過這樣的辦法把遞迴神經網路鋪開。

透過時間概念反向傳播的直觀圖解

這個很簡單的想法真的起作用了——訓練遞迴神經網路是可能的。並且，有很多人探索出了RNN在語言識別領域的應用。但是，你可能也聽說過其中的波折：這一方法效果並不是很好。為了找出原因，讓我們來認識另一位深度學習的巨人：Yoshua Bengion。大約在1986年，他就開始進行語言識別方向的神經網路研究工作，也參與了許多使用ANN和RNN進行語言識別的學術論文，最後進入AT&T; BELL實驗室工作，Yann LeCun正好也在那裡攻剋CNN。 實際上，1995年，兩位共同發表了文章「Convolutional Networks for Images, Speech, and Time-Series」，這是他們第一次合作，後來他們也進行了許多合作。但是，早在1993年，Bengio曾發表過「A Connectionist Approach to Speech Recognition」。其中，他對有效訓練RNN的一般錯誤進行了歸納：

儘管在許多例子中，遞迴網路能勝過靜態網路，但是，最佳化訓練起來也更有難度。我們的實驗傾向於顯示（遞迴神經網路）的引數調整往往收斂在亞最佳化的解裡面，（這種解）只考慮了短效應影響因子而不計長效影響因子。例如，在所述實驗中我們發現，RNN根本捕獲不到單音素受到的簡單時間約束…雖然這是一個消極的結果，但是，更好地理解這一問題可以幫助設計替代系統來訓練神經網路，讓它學會透過長效影響因子，將輸出序列對映到輸入序列（map input sequences to output sequences with long term dependencies ），比如，為了學習有限狀態機，語法，以及其他語言相關的任務。既然基於梯度的方法顯然不足以解決這類問題，我們要考慮其他最優辦法，得出可以接受的結論，即使當判別函式（criterion function）並不平滑時。

新的冬日黎明

因此，有一個問題。一個大問題。而且，基本而言，這個問題就是近來的一個巨大成就：反向傳播。摺積神經網路在這裡起到了非常重要的作用，因為反向傳播在有著很多分層的一般神經網路中表現並不好。然而，深度學習的一個關鍵就是——很多分層，現在的系統大概有20左右的分層。但是，二十世紀八十年代後期，人們就發現，用反向傳播來訓練深度神經網路效果並不盡如人意，尤其是不如對較少層數的網路訓練的結果。原因就是反向傳播依賴於將輸出層的錯誤找到並且連續地將錯誤原因歸類到之前的各個分層。然而，在如此大量的層次下，這種數學基礎的歸咎方法最終產生了不是極大就是極小的結果，被稱為『梯度消失或爆炸的問題』，Jurgen Schmidhuber——另一位深度學習的權威，給出了更正式也更深刻的歸納：

一篇學術論文（發表於1991年，作者Hochreiter）曾經對深度學習研究給予了里程碑式的描述。文中第五、第六部分提到：二十世紀九十年代晚期，有些實驗表明，前饋或遞迴深度神經網路是很難用反向傳播法進行訓練的（見5.5）。Horchreiter在研究中指出了導致問題的一個主要原因：傳統的深度神經網路遭遇了梯度消失或爆炸問題。在標準啟用狀態下（見1），累積的反向傳播錯誤訊號不是迅速收縮，就是超出界限。實際上，他們隨著層數或CAP深度的增加，以幾何數衰減或爆炸（使得對神經網路進行有效訓練幾乎是不可能的事）。

透過時間順序扁平化BP路徑本質上跟具有許多層的神經網路一樣，所以，用反向傳播來訓練遞迴神經網路是比較困難的。由Schmidhuber指導的Sepp Hochreiter及Yoshua Bengio都寫過文章指出，由於反向傳播的限制，學習長時間的資訊是行不通的。分析問題以後其實是有解決辦法的，Schmidhuber 及 Hochreiter在1997年引進了一個十分重要的概念，這最終解決瞭如何訓練遞迴神經網路的問題，這就是長短期記憶（Long Short Term Memory, LSTM）。簡言之，摺積神經網路及長短期記憶的突破最終只為正常的神經網路模型帶來了一些小改動：

LSTM的基本原理十分簡單。當中有一些單位被稱為恆常誤差木馬（Constant Error Carousels， CECs）。每個CEC使用一個啟用函式 f，它是一個恆常函式，並有一個與其自身的連線，其固定權重為1.0。由於 f 的恆常導數為1.0，透過CEC的誤差反向傳播將不會消失或爆炸（5.9節），而是保持原狀（除非它們從CEC「流出」到其他一些地方，典型的是「流到」神經網路的自適應部分）。CEC被連線到許多非線性自適應單元上（有一些單元具有乘法的啟用函式），因此需要學習非線性行為。單元的權重改變經常得益於誤差訊號在時間裡透過CECs往後傳播。為什麼LSTM網路可以學習探索發生在幾千個離散時間步驟前的事件的重要性，而之前的遞迴神經網路對於很短的時間步驟就已經失敗了呢？CEC是最主要的原因。

但這對於解決更大的知覺問題，即神經網路比較粗糙、沒有很好的表現這一問題是沒有太大幫助的。用它們來工作是十分麻煩的——電腦不夠快、演演算法不夠聰明，人們不開心。所以在九十年代左右，對於神經網路一個新的AI寒冬開始來臨——社會對它們再次失去信心。一個新的方法，被稱為支援向量機（Support Vector Machines），得到發展並且漸漸被髮現是優於先前棘手的神經網路。簡單的說，支援向量機就是對一個相當於兩層的神經網路進行數學上的最優訓練。事實上，在1995年，LeCun的一篇論文，「 Comparison of Learning Algorithms For Handwritten Digit Recognition」，就已經討論了這個新的方法比先前最好的神經網路工作得更好，最起碼也表現一樣。

支援向量機分類器具有非常棒的準確率，這是最顯著的優點，因為與其他高質量的分類器比，它對問題不包含有先驗的知識。事實上，如果一個固定的對映被安排到影象的畫素上，這個分類器同樣會有良好的表現。比起摺積網路，它依然很緩慢，並佔用大量記憶體。但由於技術仍較新，改善是可以預期的。

另外一些新的方法，特別是隨機森林（Random Forests），也被證明十分有效，並有強大的數學理論作為後盾。因此，儘管遞迴神經網路始終有不俗的表現，但對於神經網路的熱情逐步減退，機器學習社群再次否認了它們。寒冬再次降臨。

深度學習的密謀

當你希望有一場革命的時候，那麼，從密謀開始吧。隨著支援向量機的上升和反向傳播的失敗，對於神經網路研究來說，上世紀早期是一段黑暗的時間。Lecun與Hinton各自提到過，那時他們以及他們學生的論文被拒成了家常便飯，因為論文主題是神經網路。上面的引文可能誇張了——當然機器學習與AI的研究仍然十分活躍，其他人，例如Juergen Schmidhuber也正在研究神經網路——但這段時間的取用次數也清楚表明興奮期已經平緩下來，儘管還沒有完全消失。在研究領域之外，他們找到了一個強有力的同盟：加拿大政府。CIFAR的資助鼓勵還沒有直接應用的基礎研究，這項資助首先鼓勵Hinton於1987年搬到加拿大，然後一直資助他的研究直到九十年代中期。…Hinton 沒有放棄並改變他的方向，而是繼續研究神經網路，並努力從CIFAR那裡獲得更多資助，正如這篇例文（http://www.thestar.com/news/world/2015/04/17/how-a-toronto-professors-research-revolutionized-artificial-intelligence.html）清楚道明的：

「但是，在2004年，Hinton要求領導一項新的有關神經計算的專案。主流機器學習社群對神經網路興趣寡然。」

「那是最不可能的時候」Bengio是蒙特利爾大學的教授，也是去年重新上馬的CIFAR專案聯合主管，「其他每個人都在做著不同的事。莫名其妙地，Geoff說服了他們。」

「我們應該為了他們的那場豪賭大力贊許CIFAR。」

CIFAR「對於深度學習的社群形成有著巨大的影響。」LeCun補充道，他是CIFAR專案的另一個聯合主管。「我們像是廣大機器學習社群的棄兒：無法發表任何文章。這個專案給了我們交流思想的天地。」

資助不算豐厚，但足夠讓研究員小組繼續下去。Hinton和這個小組孕育了一場密謀：用「深度學習」來「重新命名」讓人聞之色變的神經網路領域。接下來，每位研究人員肯定都夢想過的事情真的發生了：2006年，Hinton、Simon Osindero與Yee-Whye Teh發表了一篇論文，這被視為一次重要突破，足以重燃人們對神經網路的興趣：A fast learning algorithm for deep belief nets（論文參見：https://www.cs.toronto.edu/~hinton/absps/fastnc.pdf）。

正如我們將要看到的，儘管這個想法所包含的東西都已經很古老了，「深度學習」的運動完全可以說是由這篇文章所開始。但是比起名稱，更重要的是如果權重能夠以一種更靈活而非隨機的方式進行初始化，有著多層的神經網路就可以得以更好地訓練。

「歷史上的第一次，神經網路沒有好處且不可訓練的信念被剋服了，並且這是個非常強烈的信念。我的一個朋友在ICML（機器學習國際會議）發表了一篇文章，而就在這不久之前，選稿編輯還說過ICML不應該接受這種文章，因為它是關於神經網路，並不適合ICML。實際上如果你看一下去年的ICML，沒有一篇文章的標題有『神經網路』四個字，因此ICML不應該接受神經網路的文章。那還僅僅只是幾年前。IEEE期刊真的有『不接收你的文章』的官方準則。所以，這種信念其實非常強烈。」

受限的玻爾茲曼機器

那麼什麼叫做初始化權重的靈活方法呢？實際上，這個主意基本就是利用非監督式訓練方式去一個一個訓練神經層，比起一開始隨機分配值的方法要更好些，之後以監督式學習作為結束。每一層都以受限波爾茲曼機器（RBM）開始，就像上圖所顯示的隱藏單元和可見單元之間並沒有連線的玻爾茲曼機器（如同亥姆霍茲機器），並以非監督樣式進行資料生成樣式的訓練。事實證明這種形式的玻爾茲曼機器能夠有效採用2002年Hinton引進的方式「最小化對比發散專家訓練產品（Training Products of Experts by Minimizing Contrastive Divergence）」進行訓練。

基本上，除去單元生成訓練資料的可能，這個演演算法最大化了某些東西，保證更優擬合，事實證明它做的很好。因此，利用這個方法，這個演演算法如以下：

1. 利用對比發散訓練資料訓練RBM。這是信念網路（belief net）的第一層。

2. 生成訓練後RBM資料的隱藏值，模擬這些隱藏值訓練另一個RBM，這是第二層——將之「堆疊」在第一層之上，僅在一個方向上保持權重直至形成一個信念網路。

3. 根據信念網路需求在多層基礎上重覆步驟2。

4. 如果需要進行分類，就新增一套隱藏單元，對應分類標誌，並改變喚醒-休眠演演算法「微調」權重。這樣非監督式與監督式的組合也經常叫做半監督式學習。

Hinton引入的層式預訓練

這篇論文展示了深度信念網路（DBNs）對於標準化MNIST字元識別資料庫有著完美的表現，超越了僅有幾層的普通神經網路。Yoshua Bengio等在這項工作後於2007年提出了「深層網路冗餘式逐層訓練（ “Greedy Layer-Wise Training of Deep Networks）」，其中他們表達了一個強有力的論點，深度機器學習方法（也就是有著多重處理步驟的方法，或者有著資料等級排列特徵顯示）在複雜問題上比淺顯方法更加有效（雙層ANNs或向量支援機器）。

關於非監督式預訓練的另一種看法，利用自動程式碼取代RBM

他們還提出了為什麼附加非監督式預訓練，並總結這不僅僅以更最佳化的方式初始權重，而且更加重要的是導致了更有用的可學習資料顯示，讓演演算法可以有更加普遍化的模型。實際上，利用RBM並不是那麼重要——普通神經網路層的非監督式預訓練利用簡單的自動程式碼層反向傳播證明瞭其有效性。同樣的，與此同時，另一種叫做分散編碼的方法也表明，非監督式特徵學習對於改進監督式學習的效能非常有力。

因此，關鍵在於有著足夠多的顯示層，這樣優良的高層資料顯示能夠被學習——與傳統的手動設計一些特徵提取步驟並以提取到的特徵進行機器學習方式完全不同。Hinton與Bengio的工作有著實踐上的證明，但是更重要的是，展示了深層神經網路並不能被訓練好的假設是錯誤的。LeCun已經在整個九十年代證明瞭CNN，但是大部分研究團體卻拒絕接受。Bengio與Yann LeCun一起，在「實現AI的演演算法（Scaling Algorithms Towards AI）」研究之上證明瞭他們自己：

「直至最近，許多人相信訓練深層架構是一個太過困難的最佳化問題。

然而，至少有兩個不同的方法對此都很有效：應用於摺積神經網路的簡單梯度下降[LeCun et al., 1989, LeCun et al., 1998]（適用於訊號和影象），以及近期的逐層非監督式學習之後的梯度下降[Hinton et al., 2006, Bengio et al., 2007, Ranzato et al., 2006]。深層架構的研究仍然處於雛形之中，更好的學習演演算法還有待發現。從更廣泛的觀點來看待以發現能夠引出AI的學習準則為標的這事已經成為指導性觀念。我們希望能夠激發他人去尋找實現AI的機器學習方法。」

他們的確做到了。或者至少，他們開始了。儘管深度學習還沒有達到今天山呼海應的效果，它已經如冰面下的潛流，不容忽視地開始了湧動。那個時候的成果還不那麼引人註意——大部分論文中證明的表現都限於MNIST資料庫，一個經典的機器學習任務，成為了十年間演演算法的標準化基準。Hinton在2006年釋出的論文展現出驚人的錯誤率，在測試集上僅有1.25%的錯誤率，但SVMs已經達到了僅1.4%的錯誤率，甚至簡單的演演算法在個位數上也能達到較低的錯誤率，正如在論文中所提到的，LeCun已經在1998年利用CNNs表現出0.95%的錯誤率。

因此，在MNIST上做得很好並不是什麼大事。意識到這一點，並自信這就是深度學習踏上舞臺的時刻的Hinton與他的兩個研究生，Abdel-rahman Mohamed和George Dahl，展現了他們在一個更具有挑戰性的任務上的努力：語音識別（ Speech Recognition）。

利用DBN，這兩個學生與Hinton做到了一件事，那就是改善了十年間都沒有進步的標準語音識別資料集。這是一個了不起的成就，但是現在迴首來看，那隻是暗示著即將到來的未來——簡而言之，就是打破更多的記錄。

蠻力的重要性

上面所描述的演演算法對於深度學習的出現有著不容置疑的重要性，但是自上世紀九十年代開始，也有著其他重要組成部分陸續出現：純粹的計算速度。隨著摩爾定律，計算機比起九十年代快了數十倍，讓大型資料集和多層的學習更加易於處理。但是甚至這也不夠——CPU開始抵達速度增長的上限，計算機能力開始主要透過數個CPU平行計算增長。為了學習深度模型中常有的數百萬個權重值，脆弱的CPU並行限制需要被拋棄，並被具有大型平行計算能力的GPUs所代替。意識到這一點也是Abdel-rahman Mohamed，George Dahl與Geoff Hinton做到打破語音識別效能記錄的部分原因：

「由Hinton的深度神經網路課堂之一所激發，Mohamed開始將它們應用於語音——但是深度神經網路需要巨大的計算能力，傳統計算機顯然達不到——因此Hinton與Mohamed招募了Dahl。Dahl是Hinton實驗室的學生，他發現瞭如何利用相同的高階顯示卡（讓栩栩如生的計算機遊戲能夠顯示在私人計算機上）有效訓練並模擬神經網路。」

「他們用相同的方法去解決時長過短的語音中片段的音素識別問題，」Hinton說道，「對比於之前標準化三小時基準的方法，他們有了更好的成果。」

在這個案例中利用GPU而不是CPU到底能變得有多快很難說清楚，但是同年《Large-scale Deep Unsupervised Learning using Graphics Processors》這篇論文給出了一個數字：70倍。是的，70倍，這使得數以周記的工作可以被壓縮到幾天就完成，甚至是一天。之前研發了分散式程式碼的作者中包括高產的機器學習研究者吳恩達，他逐漸意識到利用大量訓練資料與快速計算的能力在之前被贊同學習演演算法演變愈烈的研究員們低估了。這個想法在2010年的《Deep Big Simple Neural Nets Excel on Handwritten Digit Recognition》（作者之一J. Schimidhuber正是遞迴LTSM網路（recurrent LTSM networks）的投資者）中也得到了大力支援，展示了MNIST資料庫能夠達到令人驚嘆的0.35%錯誤率，並且除去大型神經網路、輸入的多個變數、以及有效的反向傳播GPU實現以外沒有任何特殊的地方。這些想法已經存在了數十年，因此儘管可以說演演算法的改進並不那麼重要，但是結果確實強烈表明大型訓練資料集與快速顎化計算的蠻力方法是一個關鍵。

Dahl與Mohamed利用GPU打破記錄是一個早期且相對有限的成功，但是它足以激勵人們，並且對這兩人來說也為他們帶來了在微軟研究室實習的機會。在這裡，他們可以享受到那時已經出現的計算領域內另一個趨勢所帶來的益處：大資料。這個詞語定義寬鬆，在機器學習的環境下則很容易理解——大量訓練資料。大量的訓練資料非常重要，因為沒有它神經網路仍然不能做到很好——它們有些過擬合了（完美適用於訓練資料，但無法推廣到新的測試資料）。這說得通——大型神經網路能夠計算的複雜度需要許多資料來使它們避免學習訓練集中那些不重要的方面——這也是過去研究者面對的主要難題。因此現在，大型公司的計算與資料集合能力證明瞭其不可替代性。這兩個學生在三個月的實習期中輕易地證明瞭深度學習的能力，微軟研究室也自此成為了深度學習語音識別研究的前沿地帶。

微軟不是唯一一個意識到深度學習力量的大公司（儘管起初它很靈巧）。Navdeep Jaitly是Hinton的另一個學生，2011年曾在谷歌當過暑假實習生。他致力於谷歌的語音識別專案，透過結合深度學習能夠讓他們現存的裝置大大提高。修正後的方法不久就加強了安卓的語音識別技術，替代了許多之前的解決方案。

除了博士實習生給大公司的產品帶來的深刻影響之外，這裡最著名的是兩家公司都在用相同的方法——這方法對所有使用它的人都是開放的。實際上，微軟和谷歌的工作成果，以及IBM和Hinton實驗室的工作成果，在2012 年釋出了令人印象深刻的名為「深層神經網路語音識別的聲學建模：分享四個研究小組的觀點」的文章。

這四個研究小組——有三個是來自企業，確定能從傷腦筋的深度學習這一新興技術專利中獲益，而大學研究小組推廣了技術——共同努力並將他們的成果釋出給更廣泛的研究社群。如果有什麼理想的場景讓行業接受研究中的觀念，似乎就是這一刻了。

這並不是說公司這麼做是為了慈善。這是他們所有人探索如何把技術商業化的開始，其中最為突出的是谷歌。但是也許並非Hinton，而是吳恩達造成了這一切，他促使公司成為世界最大的商業化採用者和技術使用者者。在2011年，吳恩達在巡視公司時偶遇到了傳說中的谷歌人Jeff Dean，聊了一些他用谷歌的計算資源來訓練神經網路所做的努力。

這使Dean著迷，於是與吳恩達一起建立了谷歌大腦（Google Brain）——努力構建真正巨大的神經網路並且探索它們能做什麼。這項工作引發了一個規模前所未有的無監督式神經網路學習——16000個CPU核，驅動高達10億權重的學習（作為比較，Hinton在2006年突破性的DBN大約有100萬權重）。神經網路在YouTube影片上被訓練，完全無標記，並且學著在這些影片中去辨認最平常的物體——而神經網路對於貓的發現，引起了網際網路的集體歡樂。

谷歌最著名的神經網路學習貓。這是輸入到一個神經元中最佳的一張

它很可愛，也很有用。正如他們常規發表的一篇論文中所報道的，由模型學習的特徵能用來記錄標準的計算機視覺基準的設定效能。

這樣一來，谷歌訓練大規模的神經網路的內部工具誕生了，自此他們僅需繼續發展它。深度學習研究的浪潮始於2006年，現在已經確定進入行業使用。

深度學習的上升

當深度學習進入行業使用時，研究社群很難保持平靜。有效的利用GPU和計算能力的發現是如此重要，它讓人們檢查長久存疑的假設並且問一些也許很久之前被提及過的問題——也就是，反向傳播到底為何沒什麼用呢？為什麼舊的方法不起作用，而不是新的方法能奏效，這樣的問題觀點讓Xavier Glort 和 Yoshua Bengio在2010年寫了「理解訓練深度前饋神經網路的難點」（Understanding the difficulty of training deep feedforward neural networks）一文。

在文中，他們討論了兩個有重大意義的發現：

1. 為神經網路中神經元選取的特定非線性啟用函式，對效能有巨大影響，而預設使用的函式不是最好的選擇。

2. 相對於隨機選取權重，不考慮神經層的權重就隨機選取權重的問題要大得多。以往消失的梯度問題重現，根本上，由於反向傳播引入一系列乘法，不可避免地導致給前面的神經層帶來細微的偏差。就是這樣，除非依據所在的神經層不同分別選取不同的權重 ——否則很小的變化會引起結果巨大變化。

不同的啟用函式。ReLU是**修正線性單元**

第二點的結論已經很清楚了，但是第一點提出了這樣的問題：『然而，什麼是最好的啟用函式？』有三個不同的團隊研究了這個問題：LeCun所在的團隊，他們研究的是「針對物件識別最好的多級結構是什麼？」；另一組是Hinton所在的團隊，研究「修正的線性單元改善受限玻爾茲曼機器」；第三組是Bengio所在的團隊——「深度稀缺的修正神經網路」。他們都發現驚人的相似結論：近乎不可微的、十分簡單的函式f(x)=max(0,x)似乎是最好的。令人吃驚的是，這個函式有點古怪——它不是嚴格可微的，確切地說，在零點不可微，因此 就 數學而言論文看起來很糟糕。但是，清楚的是零點是很小的數學問題——更嚴重的問題是為什麼這樣一個零點兩側導數都是常數的簡單函式，這麼好用。答案還未揭曉，但一些想法看起來已經成型：

修正的啟用導致了表徵稀疏，這意味著在給定輸入時，很多神經元實際上最終需要輸出非零值。這些年的結論是，稀疏對深度學習十分有利，一方面是由於它用更具魯棒性的方式表徵資訊，另一方面由於它帶來極高的計算效率（如果大多數的神經元在輸出零，實際上就可以忽略它們，計算也就更快）。順便提一句，計算神經科學的研究者首次在大腦視覺系統中引入稀疏計算，比機器學習的研究早了10年。

相比指數函式或者三角函式，簡單的函式及其導數，使它能非常快地工作。當使用GPU時，這就不僅僅是一個很小的改善，而是十分重要，因為這能規模化神經網路以很好地完成極具挑戰的問題。

後來吳恩達聯合發表的「修正的非線性改善神經網路的語音模型 」（Rectifier Nonlinearities Improve Neural Network Acoustic Models）一文，也證明瞭ReLU導數為常數0或1對學習並無害處。實際上，它有助於避免梯度消失的問題，而這正是反向傳播的禍根。此外，除了生成更稀疏的表徵，它還能生成更發散的表徵——這樣就可以結合多個神經元的多重值，而不侷限於從單個神經元中獲取有意義的結論。

目前，結合2006年以來的這些發現，很清楚的是非監督預訓練對深度學習來說不是必要的。雖然，它的確有幫助，但是在某些情況下也表明，純粹的監督學習（有正確的初始權重規模和啟用函式）能超越含非監督訓練的學習方式。那麼，到底為什麼基於反向傳播的純監督學習在過去表現不佳？Geoffrey Hinton總結了目前發現的四個方面問題：

1. 帶標簽的資料集很小，只有現在的千分之一.

2. 計算效能很慢，只有現在的百萬分之一.

3. 權重的初始化方式笨拙.

4. 使用了錯誤的非線性模型。

好了，就到這裡了。深度學習。數十年研究的積累，總結成一個公式就是：

深度學習=許多訓練資料+平行計算+規模化、靈巧的的演演算法

我希望我是第一個提出這個賞心悅目的方程的，但是看起來有人走在我前面了。

更不要說這裡就是希望弄清楚這點。差遠了！被想通的東西剛好是相反的：人們的直覺經常出錯，尤其是一些看似沒有問題的決定及假設通常都是沒有根據的。問簡單的問題，嘗試簡單的東西——這些對於改善最新的技術有很大的幫助。其實這一直都在發生，我們看到更多的想法及方法在深度學習領域中被髮掘、被分享。例如 G. E. Hinton等的「透過預防特徵檢測器的互相適應改善神經網路」（ Improving neural networks by preventing co-adaptation of feature detectors）。

其構思很簡單：為了避免過度擬合，我們可以隨機假裝在訓練當中有些神經元並不在那兒。想法雖然非常簡單——被稱為丟棄法（dropout）——但對於實施非常強大的整合學習方法又非常有效，這意味著我們可以在訓練資料中實行多種不同的學習方法。隨機森林——一種在當今機器學習領域中佔主導地位的方法——主要就是得益於整合學習而非常有效。訓練多個不同的神經網路是可能的，但它在計算上過於昂貴，而這個簡單的想法在本質上也可取得相同的結果，而且效能也可有顯著提高。

然而，自2006年以來的所有這些研究發現都不是促使計算機視覺及其他研究機構再次尊重神經網路的原因。這個原因遠沒有看來的高尚：在現代競爭的基準上完全摧毀其他非深度學習的方法。Geoffrey Hinton召集與他共同寫丟棄法的兩位作家，Alex Krizhevsky 與 Ilya Sutskever，將他們所發現的想法在ILSVRC-2012計算機視覺比賽中建立了一個條目。

對於我來說，瞭解他們的工作是非常驚人的，他們的「使用深度摺積神經網路在ImageNet上分類」（ImageNet Classification with deep convolutional neural networks）一文其實就是將一些很舊的概念（例如摺積神經網路的池化及摺積層，輸入資料的變化）與一些新的關鍵觀點（例如十分高效能的GPU、ReLU神經元、丟棄法等）重新組合，而這點，正是這一點，就是現代深度網路的所有深意了。但他們如何做到的呢？

遠比下一個最近的條目好：它們的誤差率是15.3%，第二個最近的是26.2%。在這點上——第一個及唯一一個在比賽中的CNN條目——對於CNNs及深度學習整體來說是一個無可爭議的標誌，對於計算機視覺，它應該被認真對待。如今，幾乎所有的比賽條目都是CNNs——這就是Yann LeCun自1989年以來在上面花費大量心血的神經網路模型。還記得上世紀90年代由Sepp Hochreiter 及 Jürgen Schmidhuber為瞭解決反向傳播問題而開發的LSTM迴圈神經網路嗎？這些在現在也是最新的連續任務比如語音處理的處理方法。

這就是轉折點。一波對於其可能發展的狂歡在其無可否認的成績中達到了高潮，這遠遠超過了其他已知方法所能處理的。這就是我們在第一部分開頭所描寫的山呼海應比喻的起點，而且它到如今還一直在增長，強化。深度學習就在這兒，我們看不到寒冬。

我們列舉了對深度學習的發展做出重要貢獻的人物。我相信我不需要再指出自從2012年以來其飛漲的趨勢了。

03 後記：現狀

如果這是一部電影，2012年ImageNet比賽將是其高潮，而現在在電影結束的時候，我們將會出現這幾個字：「他們如今在哪裡」。Yann Lecun：Facebook； Geoffrey Hinton： 谷歌； 吳恩達： Coursera、谷歌、百度； Bengi、Schmidhuber 及 Hochreiter 依然還留在學術界——但我們可以很容易推測，這個領域將會有更多的取用及畢業生。

雖然深度學習的理念及成績令人振奮，但當我在寫這幾篇文章的時候，我也不由自主地被他們所感動，他們在一個幾乎被人遺棄的領域裡深耕數十年，他們現在富裕、成功，但重要的是他們如今更確信自己的研究。這些人的思想依然保持開放，而這些大公司也一直在開源他們的深度學習模型，猶如一個由工業界領導研究界的理想國。多美好的故事啊啊。

我愚蠢的以為我可以在這一部分寫一個過去幾年讓人印象深刻的成果總結，但在此，我清楚知道我已經沒有足夠的空間來寫這些。可能有一天我會繼續寫第五部分，那就可以完成這個故事了。但現在，讓我提供以下一個簡短的清單：

1.LTSM RNNs的死灰復燃以及分散式表徵的代表

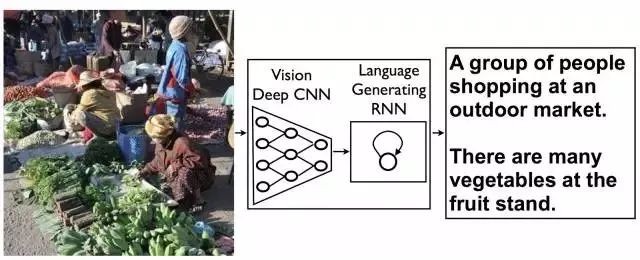
2.利用深度學習來加強學習

3.附加外部可讀寫儲存

來源：資料科學與人工智慧