(點選上方公眾號,可快速關註)
來源:校苑數模
fukugen
復原
在伊萬·費先科(Ivan Fesenko)的“科普”文章裡提到,在關於望月新一證明的討論中,有一個詞經常被提到,就是“復原”(連結:http://inference-review.com/article/fukugen)。在望月新一構建的嶄新數學體系中,他將同時附著在“數字”之上的加法結構和乘法結構拆開,將兩者各自變形,然後重新“復原”。這種做法,先從根本上消解,之後再““復原”,即使對於久經抽象推理沙場的數學家而言也相當奇怪。而望月新一的體系,正繫於這種“復原”的可行性。
如果他的體系是正確的,如果他的“復原”是成功的,這將帶來數學中代數幾何分支的變革。比如說,ABC猜想的證明。比如說,最終理解加法和乘法之間的關係。但現在,沒多少數學家能讀懂他的證明。無論證明是對是錯,也許數學界,至少是代數幾何,恐怕難以複原為以前的面貌。他的體系,他的證明,已經將數學家拆開成不同的陣營,陣營內部不斷發酵變化,引出了新的分歧。即使最後塵埃落定,得到的恐怕也只是望月新一式的“復原”。
但這就是數學前進的必經之路。
1
破題
望月新一的研究領域,是所謂的“遠阿貝爾幾何學”。如果只能用幾十字解釋這個領域的話,我只能這樣寫:
遠阿貝爾幾何學研究的是,有理數的絕對伽羅華群,以至任意代數簇的平展基本群,它們“遠離阿貝爾”的部分,也就是不符合交換律ab=ba的部分,會如何影響相應代數結構的性質。
看不懂?很正常。要解釋這個領域研究的是什麼,可能需要整整一篇文章(請參看《小朋友的塗鴉(四):一個規劃的大綱》),還不一定能解釋清楚。而為了寫這篇文章,還要找一個遠阿貝爾幾何的專家,而不是像我這樣搞組合數學的人。
是的,對於望月新一的體系,我,這篇大部分人很可能讀不懂的文章的作者,只理解一點最基礎的皮毛。對於一般人來說,我似乎是內行,但在數學界內部,我屬於吃瓜群眾。所以,如果真正的內行看到我寫錯了東西,請多多包涵。
但面對這個體系,很多數學家的境況並不比我好得多。包括菲爾茲獎得主陶哲軒,包括望月新一的恩師法爾廷斯,他們都抱怨望月新一的證明太簡略太難懂。現在,據說懂得整個證明的,除瞭望月新一之外,只有十幾個人,大部分在日本,其他在美國和法國。
大部分數學家,和這十幾個人,就是目前的兩個陣營。
2
抽象的極致
望月新一的體系,名為“宇宙際Teichmüller理論”(inter-universal Teichmüller theory),簡稱IUTT,有時候也省略對應“理論”的T,寫成IUT。
他並沒有特意發明這個略顯中二氣息的名字,這鍋要由代數幾何的先驅格羅滕迪克(Grothendieck)來背,是他發明瞭Grothendieck universe這個數學物件。而這個術語可能還要追溯到更久遠的集合論先驅,因為它對應著集合論中“所有集合組成的一堆東西”這個概念。是的,所有集合不構成一個集合,只能說成“一堆東西”,或者用“類”這個術語。幸好,中文的翻譯“全類”沒有那麼中二。用上這個翻譯的話,中文可以寫成“跨全類Teichmüller理論”。但為了原汁原味起見,我們後面還是用“宇宙”這個術語。因為,另一個universe的數學,總有些不一樣。
我們從他此前研究的最最基礎的結構,p進整數,談起。
p進整數是什麼?對於數學家來說最快捷易懂的定義,就是:
對於素數p, 的投影極限
的投影極限
我第一次看到這個定義時,一下子就讀懂了。這對數學家來說的確是好懂的定義,但對一般人就像外星語言。
絕望了?這就是我讀望月新一的論文時,從第三頁開始的感受,六百多頁之中的第三頁。
但p進整數畢竟沒那麼複雜,下麵我試著解釋一下。首先,我們來看一個p進整數的例子,取p=7,那麼下麵這幾個數都是p進整數:
……00000000000000000042
……30211045064302335342
……12450124501245012450
是的,你沒有看錯,省略號在前面。每個p進整數,都可以看成一串向左邊高位延伸至無窮的數。但它們並不是無窮,它們每個數都不相同,而這種寫法是有意義的。
在p進整數上,可以定義加法和乘法。這裡我們可以松一口氣,因為它們的計算方式跟我們熟悉的一樣(需要模p),從低位開始,然後慢慢進位計算,就像是永遠做不完的加法和乘法。減法和除法同樣由此定義。所以,p進整數跟我們熟悉的整數一樣,都有四則運算。每個整數都對應一個p進整數,只消在整數的p進位制運算式前面加上無窮個0,而它們的運算結果也與我們熟悉的運算別無二致。
奇怪的事情現在才開始。
1/5=0.2,顯然不是整數。但它是一個7進整數:
1/5 = ……5412541254125412

震驚!圖片來自pixabay
實際上,只要一個p進整數x個位不是0,那麼它的倒數也是一個p進整數。可以求倒數這一點非常重要,這意味著p進整數,或者它的推廣p進數中,擁有完整的加法和乘法結構。
奇怪的事情到這裡還沒有完。
我們可以定義p進整數的“絕對值”,或者說“大小”。我們來看看在p進整數中,幾個自然數的絕對值。我們還是取p=7為例子。
0的絕對值是0,簡直必然。
1的絕對值是1,沒有問題。
2的絕對值是1……等等,發生了什麼事?

什麼鬼……圖片來自flickr | Denise Mattox
3、4、5、6,它們的絕對值都是1。
7(也就是七進位制的10)的絕對值是1/7,突然變小了。
8(也就是七進位制的11)的絕對值是1,又回來了。接下來9、10、11、12、13的絕對值都是1。14(也就是七進位制的20)的絕對值又變成了1/7。
就這樣,如果不是7的倍數,絕對值就是1;如果是7的倍數,絕對值就是1/7。一直到49(也就是七進位制的100),它的絕對值變成了1/49。加上一的50,它的絕對值又是1。
簡單來說,對於p進整數,從個位開始有幾個0,它的絕對值就是p的幾次方分之一。對於p的冪,次數越高,數字越大,“絕對值”反而越小。
根據這個奇怪的“絕對值”,我們可以將所有p進整數看成一個空間,它的結構由這個“絕對值”,也就是兩點之間的距離給出。但這是個怪異的空間:每個三角形都是銳角等腰三角形,而如果取一個球體的話,球體中每一個點都是球心。

p進數,圖片來自Wikipedia

p進數拓撲結構的圖示,來自Wikipedia
一個自然的疑問是:這都是什麼玩意兒???
有這種疑問很正常,因為這屬於抽象而反直覺的數學。但對於數學工作者來說,這種絕對值的定義,恰好呼應了p進整數本身的定義。如果明白一開始那個一句話定義,那麼現在這個“絕對值”的概念,就會顯得順理成章,甚至非此不可。這就是對數學概念的理解程度所導致的偏差。初看似乎不明就裡的數學概念,一旦掌握了正確的思維方法,就會變得淺顯易懂。
但這又談何容易!數學是如此抽象,必須經過多年的學習,慢慢熟習它的思考方式,才能理解它的內容。
p進整數,以及它的推廣p進數,不僅在望月新一以往的工作出現,事實上,它早已是數論中常用的工具。當年懷爾斯對費馬大定理的證明也用到了p進數。望月新一此前發展的p進Teichmüller理論,則完全基於p進數,但p進數本身在這個理論中的地位,相當於高考數學中的自然數,只是最基礎的磚石。
而望月新一的新理論,“宇宙際Teichmüller理論”,又是另一個層次。他覺察到,用p進數構建的理論仍然不足以抓住他想要研究的那個數論結構,於是他另闢蹊徑,找到一個已經證明必定能抓住那個結構的數學物件,然後構建起新的數學理論,研究這個物件的性質,從而匯出他尋找的性質。這大體就是宇宙際Teichmüller理論的發展動機之一。
要構建這樣的理論,需要同時用到遠阿貝爾幾何與表示論的工具,然而這兩者格格不入,難以調和。為了折中,望月新一需要將理論的基底,也就是最基本的運算,拆成加法和乘法兩部分,將它們消解為更複雜更抽象的結構,透過這些結構的互動和變形得到想要的性質,最後證明這些結構能夠重新“復原”成某種加法和乘法。在互動和變形的過程中,他要在不同的宇宙(universe、全類)間遊走,才能得到足夠廣泛而一般的結論。加法和乘法結合起來會碰到的障礙,對於它們消解而成的結構卻不成問題,當然前提是透過恰當的變形,就像不同坐標系之間的變換。這就是為什麼望月新一要將他的理論稱為“宇宙際Teichmüller理論”。順帶一提,消解後的加法和乘法面目全非,不像通常的加法和乘法那樣基於同一套“數字”,而是形同陌路,望月新一的術語alien ring structure就由此而來。這裡的alien,並不是什麼“外星”的意思,而是取拉丁語alienus的原意“屬於他人、非自身、外來、奇怪”之義。很多地方寫的什麼“外星算術全純結構”(alien arithmetic holomorphic structure),都曲解瞭望月新一的本義。
看不懂?很正常。上面對望月新一理論的描述,來自我查閱相關資料後的總結。但要知道,我主要的研究領域是組合數學,雖然跟通常的Teichmüller理論有那麼一丁點關係,但對於一般的代數幾何,我也沒有正式學習過,只是透過閑談和閱讀懂得些皮毛。望月新一的資料,我只能抓住其中隻言片語,描繪大體的圖景。
這就是現代的數學,它研究的內容如此廣泛如此深入,一個分支上的數學家已經難以理解另一個分支的前沿,更何況是代數幾何這一最抽象的領域中耕耘的人特別少的分支遠阿貝爾幾何,它的最前沿的推廣呢?更何況這個理論是如此抽象,處理的又是如此根本的數學結果。可以說,擁有足夠的知識儲備,有充足時間能夠理解並審查望月新一理論的數學家,即使不能說屈指可數,也很可能不超過100人,這還是相當樂觀的估計。
望月新一本人這樣說過,他的理論在數學界的處境,就像數學本身在整個社會中的處境:過於抽象,以至於人們不願意去鑽研和理解。
3
爭議與迭代
一個新的證明或者理論體系,給數學界帶來重大影響,這並不是第一次。

大衛·希爾伯特,圖片來自Wikipedia
希爾伯特,就是那個提出20世紀的23個數學問題的著名數學家,他的成名之作,那篇“終結了不變數理論”的論文,在當時就引起了巨大的爭議。此前,不變數理論的大多數進展都基於具體的計算,需要給出具體的結果。這樣的證明又叫構造性證明。但希爾伯特的證明不屬此列,而分屬“存在性證明”,能斷言某個數學物件的確存在,但對於如何計算卻絕口不提。他一開始投稿恰好碰上了當時的“不變數之王”哥爾丹。哥爾丹對這樣的證明頗有微詞,他的退稿評價是:
這不是數學,這是神學。
但最終希爾伯特幸得克萊因的保薦(“這無疑是這本雜誌發表過有關一般代數的最重要的工作”),論文得以發表。正因為無需具體給出構造,存在性證明要比構造性證明要更為簡潔有力,也因此逐漸被廣泛接受。即使是一開始拒稿的哥爾丹,最後也承認了希爾伯特的工作,“即使是神學也有其價值”。希爾伯特之後也因為公理化的工作以及其他數學成就,躋身當時數學界的頂尖。
另一位為數學界作出巨大貢獻的德國數學家康託爾,他的命運卻大不相同。在研究傅裡葉分析時,康託爾領會到無窮之後仍有無窮的無窮。他從最基礎的集合論開始,建立了一個全新體系,描述了超越無窮的無窮,也就是超窮。集合論中的很多基礎結果,就出自他的手筆。

格奧爾格·康託爾。圖片來自Wikipedia
但他的研究甫一發表,就遭到許多頂尖數學家的攻訐。龐加萊說他的想法就像“嚴重的疾病”,正在感染數學這一學科。當時執德國數學界牛耳的克羅內克,公開反對康託爾關於超窮的理論,甚至到達了人身攻擊的地步。他稱康託爾為“科學騙子”、“背叛者”、“腐蝕了青年”,近乎偏執地指責著康託爾和他的理論。
但數學畢竟是數學。經過曲折發展之後,集合論成為了現代數學的基礎,成了數學系學生的必修課。正是希爾伯特作出了這樣的斷言:
身處康託爾跟我們一道展開的天堂內,我們屏息於驚嘆之中,知道無人能將我們由此驅逐。
但康託爾本人的命運,卻遠沒有那麼光明。也許是因為得不到理解,也許是因為這些無休止的攻擊,康託爾患上了抑鬱症,一直沒有痊癒。他的晚年恰逢第一次世界大戰,貧困加劇了戰爭帶來的飢謹。心臟病給他的最後一擊,也許是種解脫。
一個人的命運,即使有再多的自我奮鬥,始終逃不出歷史的行程。領頭人的個人好惡,足以令一個人萬劫不復。即使他的理論被廣泛接受,在生前領受過榮耀,也不過如此。

亞歷山大·格羅滕迪克,圖片來自上沃爾法赫數學研究所(Mathematisches Forschungsinstitut Oberwolfach)
格羅滕迪克的遭遇,處於康託爾和希爾伯特之間。他的數學風格高度抽象,但卻能得出實際的結果。取用我之前寫的文字:
他談論的數學實在過於抽象,難以理解。但這就是格羅滕迪克做數學的風格:盡可能從數學物件中將不必要的細節抽象出來,抽象得一般的數學家都會以為剩下的只有“虛空”,然而他仍然能從“虛空”中抓住某些東西,從而建立他的理論,完成他的證明。用格羅滕迪克本人的說法,如果把數學問題比作堅果,大部分數學家做的就是用鎚子和鑿子把堅果鑿開,而他的做法則是將堅果浸在水裡,慢慢軟化它的外殼,又或者讓它經受風吹日曬,然後等待合適的時機,堅果自然就會裂開。
對於大部分數學家來說,這個過程太漫長,也許只有擁有深刻洞察力的格羅滕迪克,才能在能接受的時間內,用這種方法解決問題。這也是他的數學難以被理解的原因之一:他幾乎不考慮具體的示例,都是從盡可能抽象的角度出發,思考支配某個數學問題背後的宏大數學結構。有時候這也會鬧出笑話。有一次討論數學的時候,有人向格羅滕迪克提議考慮一個特定的質數作為例子。“你的意思是找一個真實的數字?”格羅滕迪克有點疑惑。對方點了點頭。他回答:“好吧,我們考慮57這個質數。”57當然不是質數,但格羅滕迪克大概沒有註意這一點,他從來不考慮具體的例子,一切從抽象出發。
格羅滕迪克的這種風格,讓他年紀輕輕就全套改寫了代數幾何所用的數學語言,給這個領域帶來了全新的抽象思維方式,讓代數幾何成為數學中可能是最抽象最深奧但也最有力量的分支。
但在他提出所謂的“標準猜想”之後,情況悄然改變。格羅滕迪克提出這一系列猜想,是為了闡明某些非常深層次的算術結構的存在性,一旦這些猜想得到證明,許多數論中的猜想,比如韋爾猜想,也能得到解決。不幸的是,由於標準猜想本身過於抽象,處理的問題過於廣泛,所以久攻不下。雪上加霜的是,他的學生德利涅繞過了標準猜想,取道更“經典”也沒那麼抽象的技巧完成了最後一個韋爾猜想的證明。這就使很多人的註意力從標準猜想上移開,他之後寫出的研究綱領也應者寥寥。最後,他慢慢隱退到比利牛斯山脈之下,在前不久成為了歷史。
但格羅滕迪克畢竟留下了龐大的數學遺產。他編寫的EGA和SGA是代數幾何的入門寶典,他的定理和想法,尤其是標準猜想,仍然留在眾多代數幾何學者的心頭。
當然,新理論新證明被徹底摧毀的例子也比比皆是。在2004年,美國數學家路易·德·布朗奇(Louis de Branges)在自己的個人頁面上貼出了一篇124頁的論文,聲稱利用自己發展的基於希爾伯特空間的一套體系,證明瞭數論中最引人註目的黎曼猜想,跟望月新一的情況相當相似。因為德·布朗奇此前曾證明另一個著名猜想——比伯巴赫猜想(Bieberbach conjecture),所以也有人關註他的證明。但直至現在,論文經過多次修改,似乎仍然站不住腳。目前數學界普遍認為他並未能證明黎曼猜想。
不停有人提出新的想法,即使一開始不被接受,歷經時間洗練,終將得到應有的評價,而數學也就此進步。雖然提出新想法的人,他們各自有需要承受的命運,不以他們的貢獻為轉移。這就是數學史。
而望月新一的理論,就是在當下展開的歷史。他的理論是對是錯,只能拭目以待。
4
理論的滲流
聞道有先後,術業有專攻。
新理論總有個滲透的過程,即使是相應領域的專家,也不可能一下子全部理解。而現代數學高度專業化的體系,更使不同分支的數學家難以相互理解。望月新一之前耕耘於代數幾何中的遠阿貝爾幾何,但代數幾何方向甚多,而遠阿貝爾幾何又是一個少人問津的領域,能評判望月新一工作的專家,不消說是少之又少。雪上加霜的是,望月新一這次提出的新理論不僅僅是遠阿貝爾幾何,而是它的延伸,再加上高度的抽象性和龐大的頁數,足以令一部分專家望而卻步。
但新理論的確有其吸引力。望月新一本人在代數幾何這個領域早已名聲在外,他在1996年就證明瞭格羅滕迪克提出的一個有關遠阿貝爾幾何的猜想,還因此被邀請在1998年的國際數學家大會上作45分鐘演講。既然他之前的工作證明瞭他有如此能力,那麼他的新工作當然也值得認真對待。何況,望月新一宣稱他的新理論能夠用於證明數論中懸而未決的ABC猜想,這就更讓人期待了。
有些數學家被新理論所吸引,花了大量時間研讀,自覺理解了箇中真諦,成為了為新理論搖旗吶喊的人。
有些數學家同樣被新理論說吸引,花了大量時間研讀,但感覺還是解釋不清,難以理解。
有些數學家對新理論有興趣,但沒有時間研讀,只能交給別的專家。
有些數學家不懂這個分支,只能圍觀。
望月新一的“宇宙際Teichmüller理論”(IUTT),就這樣將數學界分成了兩大陣營:覺得自己讀懂的,還有覺得自己沒懂的。圍觀群眾不在此列。
覺得自己讀懂了的數學家,他們在積極地宣傳這個理論,想讓更多的人理解它。伊萬·費先科也是其中一員。近年來,在世界各地召開了數次討論IUTT的研討會,費先科有不少牽線搭橋之功。他和其他數學家也撰寫了不少介紹IUTT的文章和綜述,試圖用不同的視角來講述這個理論。
覺得自己沒有讀懂的數學家,有的仍在努力研讀,有的嘗試用自己知道的數學方法來從側面驗證IUTT的正確性;也有的已經放棄,轉而對IUTT的正確性產生了懷疑。
每個新理論都會經歷這個階段,這個等待驗證的階段。只有經過這個階段,等到大部分專家接受它的正確性,新理論才算是正式確立,數學也得以進步。
只是,對於IUTT來說,這個階段似乎太長了一點。
同樣是代數幾何中的新突破,另一位數學家彼得·索爾策(Peter Scholze)在2011年前後提出的perfectoid空間,很快就被數學界所承認,證據就是他從2012開始獲得的一系列殊榮。要知道,他提出這個理論的時候還只是博士生,但在2012年答辯之後,沒過多久就被母校波恩大學重新聘請為教授,以24歲的身份創下了德國史上最年輕教授的記錄。熟悉德國教育系統的人,會更感嘆他的成就,因為在德國,教授的地位很高,聘請的條件也因此非常苛刻。這更凸顯了他的成就。

彼得·索爾策。圖片來自Wikipedia
那麼,索爾策和望月新一,兩人的理論為何遭遇迥異?
索爾策的理論處於代數幾何研究的主流,能理解的專家人數比較多,而望月新一的理論則不算主流,專家也比較少。有時候人多人少,也能決定理論被接納的速度。索爾策的理論包含的新意,很快就能被讀懂並應用到新的問題上;望月新一的IUTT則是全新的系統,略有格羅滕迪克的遺風,看起來波瀾不驚,但結論出人意料,需要吃透整個系統,才能判斷最後的證明是對是錯,但過於渾然一體,也讓別人難以進行旁敲側擊式的驗證,偏偏這種驗證也正是考驗新理論最快的方法。
對於望月新一來說,這些都是非戰之罪。雖有忮心,不怨飄瓦。
但望月新一自身也並非毫無責任。對於現代數學家的標準而言,他的個性也稍有乖張之處。即使他曾經在美國生活過,在回到日本之後,他就很不願意到海外與其他數學家交流。他並非不樂意交流,證據就是在2016年的一次IUTT研討會上,他曾透過影片通話接入會場,為與會數學家解答一些疑難問題。而他窩在京都長時間自己搗鼓這一套理論,也不是數學界通常的做法。一般來說,數學家至少會跟同一個實驗室的同事討論相關問題,在討論之中,可以獲得更多靈感,也能藉此檢驗理論是否正確,或者投石問路,看看是此路不通還是大有可為。上一個口風像望月新一那麼嚴的,還是證明瞭費馬大定理的懷爾斯。當然,數學家經常開學術會議互相交流,少不免走漏風聲。我當然不知道望月新一有沒有跟同事討論,很可能有但是同事的保密工作做得很好,也許沒有但這個可能性很低,又或者關註遠阿貝爾幾何的人實在少。但結果就是,當這個證明出現之時,人們毫無心理準備。
另一個可商榷之處,就是他在公開他的理論時,沒有選擇數學界一般會使用的預印本網站arXiv,而是直接放到了自己的個人頁面上。當然,論文放到什麼地方,這是他的自由,但也使數學界不能及時瞭解他的理論。不過話又說回來,這項工作引起的轟動,也很快讓他的論文為數學界所知,所以其實問題也不大。
可以說,他的個性或者說偏好,在客觀上的確阻礙了他與同行之間的交流。
結果就是,現在即使接受IUTT的專家越來越多(對於一個相對冷門的領域來說,十幾個專家不算少數),但這些專家相當一部分是望月新一在日本的同事,還有過從稍密的同行。當然,也有相對獨立的學者認為他們同樣搞懂瞭望月新一的證明,但人畢竟也會犯錯,很多旁觀的數學家認為,現在認同的人數還不夠多。
數學這門學科雖然有無可辯駁的邏輯作為守門人,但它仍然是一種人類活動。新理論無論是對是錯,總要有足夠的人承認,才得以確立。確立後的理論也不一定正確,確立後被推翻的證明雖不多,但也有。只有當大部分專家都理解了這個理論,再也挑不出毛病,從而站到了“自認為懂”的陣營裡,甚至能由此生髮出新的結果,理論才算真正確立。沒有相應專業知識,或者不肯花時間的人,都只是局外人,沒有權利對理論的正誤說三道四。
但事情畢竟在進展。據說,目前IUTT的四篇論文中,前兩篇構建的體系已經被許多專家認為成立,即使是那些覺得沒有讀懂整個證明的專家。目前爭議的焦點之一,在於第三篇論文的推論3.12,也就是Szpiro猜想的證明關鍵。Szpiro猜想能推出ABC猜想,也難怪大家特別關註這個推論。據說,在之前的版本,推論3.12的證明只有幾行,語焉不詳,但我看到的幾天前(2017-12-14)的新版本中,望月新一加上了好幾頁的註解。我只能希望這些註解能消除某些專家的疑惑。
發表與審閱
在驗證證明的這個節骨眼上,從日本傳來了一段詭異的新聞:據說望月新一關於ABC猜想的論文即將發表,發表的期刊是《數理解析研究所公刊》(Publications of the Research Institute for Mathematical Sciences),簡稱PRIMS。

歐洲數學協會網站上有關PRIMS雜誌資訊的截圖
這段訊息來自日本的《朝日新聞》,算是老牌媒體,而且近水樓臺,也難怪訊息出來之後,引起了數學界的轟動。
在數學界,評定一個證明是否正確的標準之一,就是“在同行評議的正規學術期刊上發表”。要想做到這一點,就要把論文寄到期刊的編輯部(現在通常用網頁系統),接受之後的一連串審核。
首先,編輯部在接到論文之後,會指派一位相關領域的編輯處理這篇論文。個別期刊可以由作者指定編輯。編輯會先進行初審,初步考量這篇論文是否適合在本期刊發表。絕大部分明顯有問題的論文會在這一步被篩選排除。這一步不需要花多少時間。
然後,編輯會指定幾位較為資深、在論文相關領域中有過貢獻的同行,邀請他們進行審稿。這一步主要是審查證明的正確性和內容的原創性。到底選幾位,不同的期刊面對不同的文章也有所不同。有單選一位的,也有12人委員會的先例,但大多數情況是兩到三位。審稿人精讀論文之後,會給出各自的意見,編輯負責將這些意見整合,得出一個結論。結論有這幾種可能:拒稿、大修(major revision)、小修(minor revision)、發表。如果結果是拒稿或者發表,審稿人的工作就此完成;否則,編輯會將審稿人的意見和結論發給論文作者,讓作者進行修改後,提交新的版本。新的版本會讓審稿人重新審讀,如此往複,直到最終拒稿、最終發表或者作者自行撤回論文。
這也是論文發表需時最長的階段。越好的期刊,能請到的審稿人水平越高,審理也越嚴格。因為要有深入的理解,才能判定正確性,所以審稿人通常會花上很長的時間來審讀,確保每個細節都沒有問題。我自己當然投過稿,每次審稿意見回來都會驚嘆於審稿人的細緻,許多細微的筆誤都會一一指出;我自己也替一個不算特別好的期刊審過稿,精讀那篇論文花了我一個月電車上下班的時間,那還只是一篇十幾頁的文章。正因為嚴格,所以來來回回拖上三四年的例子也不算罕有。
這就是論文發表能作為金標準的原因之一:能發出來,證明至少有兩三個跟你沒什麼關係的同行,差不多理解了你的論文,而且相當細緻地確認了你的證明是對的。一般來說,無法透過這一階段的論文並不多,因為大多數數學論文在投稿之前,作者都會先與同事交流,再於預印本網站(如arXiv)發表,也會在一些學術會議上宣講。如果論文有嚴重的問題,通常在這些階段的交流之中就會被指出。作者敢於投稿的,大部分都起碼不會有嚴重的問題。
這場審稿的拉鋸戰,最大的得益者是之後希望研讀的數學家。既然已經有人讀過,說明論文是可以理解的,而拉鋸過程中作者對論文的修改,更會讓其中的理論和證明更易於理解。可以說,審稿人、編輯和作者在這個階段的來來回回,就是在不斷打磨論文字身,使其更晶瑩通透,能讓人一覽無遺。
最後,編輯在得出結論後,如果決定這篇文章可以發表,那麼就會將文稿交給出版社的編輯,進入最終的文稿編輯流程。值得一提的是,在整個過程中,無論是編輯還是審稿人,他們所做的大量工作,全都一文不取。
但望月新一這次卻有點蹊蹺,因為望月新一的工作單位,正是數理解析研究所,而他本人,就是PRIMS這個期刊的主編。一時輿論嘩然,很多人覺得,這種行徑可能在倫理上說不太過去,有些人更是作起了無端的惡意猜測。
因為新聞實在太大,Nature的Davide Castelvecchi給PRIMS編輯部發了一封電子郵件求證,而PRIMS很快作出了回應:
望月教授有關宇宙際Teichmuller理論的幾篇論文仍未被期刊接收發表,因此我們很抱歉,RIMS無法對此評論。
The papers of Prof. Motizuki on inter-universal Teichmuller theory have not yet been accepted in a journal, and so we are sorry but RIMS have no comment on it.
措辭很審慎,也有點奇怪。根據最後一句,期刊的回覆似乎站在RIMS,也就是數理解析研究所的立場。這樣的話,難以判斷望月新一的論文是否的確投給了PRIMS。但如果這些論文不在PRIMS手頭上的話,那麼他們又如何知道論文仍未被接收發表,也就是說仍未透過審議過程呢?但望月新一本人就是主編,他自己肯定知道自己論文的情況,所以也不能排除論文沒有投到PRIMS,而是望月新一本人或者知道內情的同事所作的回覆。
這也難怪望月新一不喜歡媒體。在他的主頁底部,有一句話,用很大的藝術字型寫著:本站點的內容和圖片不得用於媒體報道。所以,這篇文章不能有他的照片。看看現在,新聞即使在日本發表,在不當的翻譯下,傳來傳去也惹出了大風波。
但即使望月新一的確將論文投到了PRIMS,一般來說也無需擔心利益衝突的問題。原因之一,是數學界早已有一套相當完備的系統,用以避免利益衝突。在選定編輯和審稿人時,一般來說,與任何一名作者在五年內合作發表過文章的,指導過任何一名作者研究的,還有與任何一名作者共處一個實驗室甚至一個學校的,為了避嫌都不能參與。有些領域研究的人太少,要是全避嫌了可能也不剩什麼人,這時候編輯也會慎之又慎,有時候甚至會為了避嫌,邀請研究領域稍遠,但可能對論文內容有所瞭解的研究人員進行審稿。即使是主編,這套系統也會照常運作,不給情面。
也許你會說,那既然望月新一本人是主編,那麼他不是更應該避嫌,不要將論文投到PRIMS,以免瓜田李下?我覺得他也許就是這樣做的,因為我們還不知道他論文的去向。但也有一種可能,就是他並不在意論文在什麼地方發表。畢竟他已經釋出了自己的新理論,也吸引了專家研讀。證明是否正確,領域內部自有定奪。即使投稿,也不過是一種尋找審讀者確認的方式。在哪個期刊,並不重要。數學界也瞭解現在的情況,所以只是頗有微詞,並沒有群起而攻之。
說一點我個人的想法。我個人完全不擔心望月新一所謂的利益衝突和學術倫理問題,最大的理由就是他沒有動機。他已經功成名就,不需要什麼文章。數學這種東西,對就對,錯就錯,不存在編資料或者實驗造假,一切細節都在文章裡。要是錯了,無論強行發表在什麼期刊上,也終有一天會被髮現,而一發現就無可抵賴,只能重新修補。而且數學家對於證明的疑心很重,甚至到了偏執的地步。別人可能覺得差不多對了,數學家考慮的卻是有什麼地方可能出問題。在這種高標準下,疏失犯錯固情有可原,故意造假則得不償失。另外,正常的學術評價體系也不會過多考慮文章的發表,而是會綜合考慮同行的評價,多發幾篇文章並沒有什麼用。況且,一個造假髮現就會身敗名裂,甚至有人會以死謝罪的國家和體系,我覺得不能跟大部分讀到這篇文章的人身處的環境相比。很多人的擔憂,也許只是從此處自身感受作出的一種投射。
對於數學來說,文章發表並不是研究的終點。尤其是對於像望月新一的新理論那樣重要的結果而言,數學家會前僕後繼地研究它、理解它、挑剔它,嘗試在其上生髮出新的結果,或者找出它的錯誤。廣中平佑當年需要兩百多頁才完成的奇點消解定理,在經過許多數學家的理解和簡化之後,現在有了不少的簡化證明,其中有些只需要二十頁,原來的十分之一,而數學界對奇點消解的理解也遠勝以往。數學是活著的,數學有它的生命,而發表並不是它的終點。
當然,我不是說數學家都白璧無瑕。數學界自有它的陰暗角落,就算是“自認為懂”望月新一新理論的陣營內部,也有各種奇怪的事情在發生,而兩個陣營之間的爭吵也很有難說謙謙君子之處。但證明總在日光之下。
況且,做純數學的人,如果沒有一點熱愛數學的心,恐怕也很難久坐數學研究這一錢少活難的冷板凳。也許望月新一併不介意數學界甚至他自己領域之外的人如何看待他。他只要能做出好的數學,就可以了。
想想佩雷爾曼。
6
證明與理解
從目前的跡象來看,望月新一應該已將論文投向某個學術期刊,而且也應該斷斷續續收到了一些審稿意見,間接證據就是他的論文不斷在更新,當然大多數是他與同事同行討論的結果,但一些澄清概念的註解也很有可能是為了回應審稿的意見而寫下的。
那麼,如果期刊收到像望月新一的論文那麼難讀的投稿,應該怎麼審稿?
世上數學家不少,總有幾個在相關的研究領域鑽研。如果投稿處在期刊的專業範圍內,那麼編輯肯定能找到能夠審核論文的專家。當然,專家是否願意審稿又是另一回事,但只要接受了審稿,那基本的專業素養就有了保證。既然審稿人是專家,就不會完全讀不懂。也許會有一些不太理解的地方,但這時審稿人可以透過編輯向作者反映情況,要求更詳細的解釋。這樣一來二去,慢慢地也就讀懂了,可以作出評判。論文的終審稿通常會比初稿容易理解得多,這就要歸功於審稿人、編輯和作者的共同努力。
當然,論文有兩種難度。有些論文,例如佩雷爾曼對龐加萊猜想的證明,本身不長,但是因為高度抽象,以及作者各種跳步省略,導致文章極其難讀。有些論文,例如Almgren某篇關於幾何測度論的論文,本身就很長,一共1728頁,差不多是望月新一四篇論文合計頁數的三倍。這麼長的文章,即使不需要檢查正確性,慢慢地讀下去也很費勁。
望月新一的論文也許兩種難度兼具,但原則上並非不可逾越。不要低估數學家的耐心。
那有沒有可能作者也沒有辦法解釋,導致專家也不明白呢?
你可能會覺得,作者不也是人麼,只要是人,就肯定有辦法解釋啊。人又不是機器。
對啊,但如果機器也參與了證明呢?
這就是計算機輔助證明,雖然稀少,卻也存在。最有名的例子就是1976年美國數學家阿佩爾和哈肯對四色定理的證明。

法國大區的四色染色,圖片來自Wikipedia
四色定理,說的是任何地圖都能用四種顏色塗抹,使得相鄰的區域顏色不同。這個陳述看起來人畜無害,似乎不難解決,而許多知名的數學家也被它的外表迷惑,比如閔可夫斯基就曾在課堂上誇下海口,一邊說這個問題沒被證明只是因為沒有一流數學家去做,一邊就在黑板上開始推導,推了一節又一節課,最終只能食言。當然,哥德巴赫猜想和費馬大定理看起來也人畜無害,這也不妨礙它們難倒一大片頂尖數學家。但與兩者不同的是,四色定理的證明很難說是重大突破。它屬於組合數學,但這個領域因為著眼點相當分散,能統領一大片不同課題的體系少之又少。
阿佩爾和哈肯的證明被歷史記住,主要因為這是第一個計算機輔助完成的重大證明。他們的證明基於所謂的“放電法”。首先,他們利用計算機,設計了一些“放電規則”,這些規則能用於證明任意的平面地圖必然包含1936種構型之一。這1936種構型,又被稱為放電規則對應的“不可避免構型集”。然後,他們利用計算機證明瞭,所有這1936個構型都是可以約化的。也就是說,所有平面地圖都能被約化,變成區域數更少的平面地圖,而小地圖能用四色染色,當且僅當大地圖同樣如此。如果存在不能用四色染色的平面地圖,取這種地圖中區域數最少的地圖,透過約化,能匯出區域數更少但同樣無法用四色染色的地圖,引發矛盾。阿佩爾和哈肯就是這樣,證明瞭四色定理。
但這篇論文卻讓想要驗證的數學家犯了難。論文由兩種截然不同的體裁合成:數學家熟悉的人工證明,還有計算機熟悉的計算過程。人工證明雖然繁複,但還在數學家熟悉的範疇裡。但計算機的計算過程應該怎麼驗證呢?
雖然具體的演演算法屬於人工證明的部分,但機器畢竟不認識演演算法,它只認識能執行的程式碼,所以還要驗證具體的演演算法實現程式碼是否正確。而從程式碼到具體的運算結果,又是另一回事,雖然原則上可以逐一驗證,但長度實在超出了人類能接受的範疇。但不去驗證具體的計算,又如何能確定所有結果都準確無誤?也許有些編寫上的細節沒有註意到,或者當時計算的硬體有問題?
所以這個證明的驗證,花了很長時間。
驗證所有構型都能被約化的部分相對簡單。雖然計算量大,但這主要用於尋找具體的約化方法,驗證約化成立倒是不費多大功夫。為了檢查,可以重新由不同的人在不同的硬體上用不同的語言重新編寫這部分的程式碼,然後進行計算。一次計算可能有問題,但兩次細節完全不同的計算同時出錯的可能性就低得多。
問題是驗證放電規則和不可避免構型集。計算部分由電腦完成,但驗證卻必須手工進行。如此龐大的證明,一開始有漏洞幾乎是必然的。在幾年後,德國的一位碩士生檢驗了整個證明的40%,發現在放電規則中有一個嚴重錯誤。其他人也陸續發現了一些小問題。阿佩爾和哈肯花了不少時間處理這些問題,最後出版了一本專著,共計七百多頁。隨後,許多數學家陸續嘗試簡化這個證明,提出了許多不同的證明。雖然這些證明都需要計算機的輔助,但畢竟這麼多獨立證明全都出錯的可能性很小,大家也就都接受了四色定理。
另一個受到類似“禮遇”的,是託馬斯·黑爾斯(Thomas Hales)對開普勒猜想的證明。他證明的是,在三維空間中堆砌大小相同的小球時,最密集的方式是面心立方和六方最密堆積。
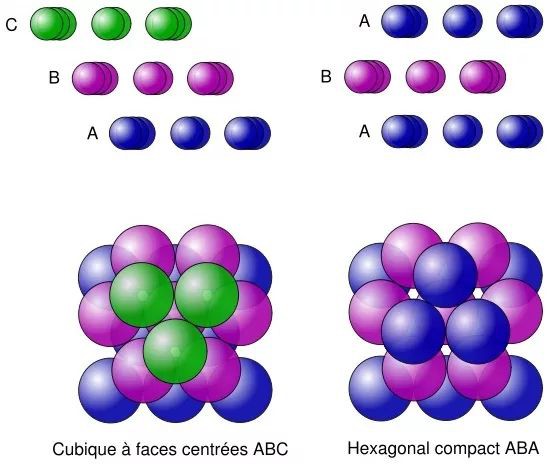
兩種最密堆積,圖片來自Wikipedia
黑爾斯的證明可謂暴力窮舉的典範。他利用計算機,將所有可能的情況一一分類,總數超過五千,然後利用計算機演演算法逐一否定這些可能性,這需要解開共計約十萬個線性規劃問題。如果沒有計算機,這恐怕是不可能完成的任務。證據就是,最終證明共計250頁,卻還要外加3GB的計算機程式和資料。
由於開普勒猜想的重要性,黑爾斯的證明也相當引人註目。他將論文投到了數學界的頂級期刊《數學年鑒》(Annals of Mathematics)。在數學界,只要你說出Annals這個詞,人人都知道你指的是《數學年鑒》。編輯部自然也不敢怠慢,畢竟這是個長久懸而未決的猜想,而計算機在證明中的角色無比重要,編輯也希望能完全確認計算正確性。他們組織了一個12人委員會來審查這篇文章,只有12個人意見完全一致,這篇文章才算透過。為了詳細驗證整個證明的正確性,有些委員還在自己的實驗室裡召開了研討班,準備細細檢查證明的方方面面。
委員會花了4年,結論是他們“99%確定”證明是正確的。他們雖然完成了大部分證明的檢查,但仍未到徹底的地步。以數學家的標準來說,這還是不太令人滿意,但證明太長太麻煩,委員們實在乾不動了。最後,《數學年鑒》發表了這篇審稿標準史無前例,審稿結果也史無前例的文章。
這些計算機輔助證明,即使計算機只起到了輔助計算的作用,也足以讓希望確認證明正誤的數學家煩惱不已。這麼長的計算,人花一輩子也不可能完全驗證,怎麼才能確定計算沒有出錯?
既然人不能驗證,那麼機器怎麼樣?
只要將證明完全形式化,寫成機器能明白的格式,那麼就可以讓機器去驗證整個證明。好在驗證總不會比計算難,既然機器能完成計算,那麼也能完成證明。於是,要確認形式化證明的正確性,只需要先讓機器去驗證,然後人工檢查機器驗證程式碼的正確性。這樣的程式碼通常很短,而且可以用於許多證明,可以說用力少而建功多。
問題在於,證明的精華部分是由人類完成的,而人類的語言機器顯然讀不懂。要想讓機器驗證證明,就要把這部分完全形式化。這是個艱巨的工作。
對於四色定理和開普勒猜想的證明,因為它們非常重要,所以即使明知很難,數學家還是去做了。2005年,Werner和Gonthier給出了四色定理的一個完全形式化的證明,並用軟體Coq完成了驗證。從2003年開始,黑爾斯開始了一個合作專案Flyspeck,旨在將他自己的證明完全形式化,然後用機器來檢驗,從而確立證明的正確性。與21位合作者花了十一年多的時間,他終於完成這個專案,而現在開普勒猜想已被公認獲得證明。(關於形式證明,請參見木遙的《形式證明:機器的光榮與人的夢想》)
所以說,即使讀不懂,還是有辦法審稿。當然,需要如此大費周章的論文少之又少,也只有非常重要的論文才會獲得這種待遇。但數學家對證明正確性的執著,由此可見一斑。
但對很多數學家來說,知道一個證明站得住腳還不夠,他們希望能*理解*整個證明。對於四色定理和開普勒猜想的證明,他們也許會說:“好,我知道那是對的,但它*為什麼*對?”
這種對理解的渴求,也是推動數學前進的動力。數學家追求證明,但從來不單追求證明。他們的真正目的,是透過證明去理解為什麼這個定理是對的,為什麼那個理論要以如此方式建立。機器證明也是數學,但談不上是好的數學,或者更準確地說,談不上是美妙的數學。
也許終有一天,人工智慧也會懂得做數學,它們也許會擁有能大幅拋離我們的能力。就像薑峰楠(Ted Chiang)的短篇科幻《人類科學之演化》(The Evolution of Human Science,首發於《自然》期刊)那樣,也許有一天,人工智慧做的數學會達到人類無法理解的地步,僅僅皮毛也足以讓人類最頂尖的數學家鑽研一生。當然,原著中擁有超人能力的並非人工智慧,而是植入晶片的人類,但道理是一樣的。
然而,即使人工智慧超越了我們,對數學的理解以及它給我們帶來的美感也不會消失。我們做數學,為的不僅是追求真理,還為了理解這些真理。
而望月新一的證明,只是歷史長河中前僕後繼的又一步。
7
後記
我一直覺得,寫這篇文章的不應該是我。我做的是組合數學,對於代數幾何所知甚少,寫關於望月新一的文章,簡直是趕鴨子上架。
但瞭解更多的人在哪裡?
比我更懂的人肯定多得是。任何一個做代數幾何的博士生,肯定都比我更適合寫這篇文章。但似乎沒有聽見他們的聲音。
我理解他們。這畢竟是一個高度抽象的學科,要向研究方向不同的同事解釋尚且很有難度,更何況向一般人解釋?
這也許也是望月新一拒絕媒體的理由。媒體肯定不懂他的理論,只知道這可能是一個重大突破,可以搞個大新聞。但這些媒體何嘗願意瞭解他的理論?寫成報道,焦點多半在個人的私生活上,要麼就是各種八卦。看的人是很多,但看完之後,給人們又留下了什麼教益?
但這個事情畢竟不能不做。正如他的新理論也需要知音來幫助宣講,數學本身也要靠科普才能傳播,人們才會認識到數學的重要性,而不是問出“微積分有什麼用,又不能買菜”這種問題。懷有惡意的媒體固然會斷章取義,但讓更多人更瞭解數學的美妙也是件好事,值得再三權衡。
這篇文章,由於本人知識所限,難免有許多疏漏,權當拋磚引玉。希望與遠阿貝爾幾何關係更密切的專業人士,能寫出更深入準確的文章,讓大家分享數學最前沿的這一大事。
參考文獻:
1、Ivan Fesenko, Fukugen, Inference Review, http://inference-review.com/article/fukugen
2、Mochizuki Shinichi, Inter-universal Teichmuller Theory I: Construction of Hodge Theaters, http://www.kurims.kyoto-u.ac.jp/~motizuki/Inter-universal%20Teichmuller%20Theory%20I.pdf
3、Mochizuki Shinichi, The Mathematics of Mutually Alien Copies: From Gaussian Integrals to Inter-universal Teichmüller Theory, http://www.kurims.kyoto-u.ac.jp/~motizuki/Alien%20Copies,%20Gaussians,%20and%20Inter-universal%20Teichmuller%20Theory.pdf
【關於投稿】
如果大家有原創好文投稿,請直接給公號傳送留言。
① 留言格式:
【投稿】+《 文章標題》+ 文章連結
② 示例:
【投稿】《不要自稱是程式員,我十多年的 IT 職場總結》:http://blog.jobbole.com/94148/
③ 最後請附上您的個人簡介哈~
覺得本文有幫助?請分享給更多人
關註「演演算法愛好者」,修煉程式設計內功
 知識星球
知識星球
