(給演演算法愛好者加星標,修煉程式設計內功)
轉自:阮一峰的網路日誌
統計學裡面,正態分佈(normal distribution)最常見。男女身高、壽命、血壓、考試成績、測量誤差等等,都屬於正態分佈。
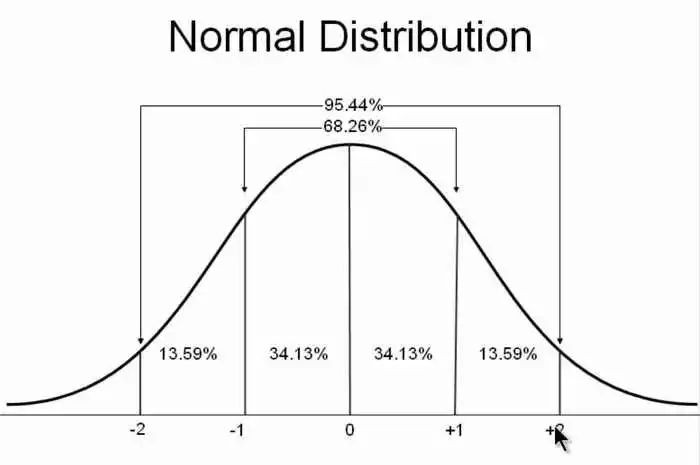
以前,我認為中間狀態是事物的常態,過高和過低都屬於少數,這導致了正態分佈的普遍性。最近,讀到了 John D. Cook 的文章,才知道我的這種想法是錯的。
正態分佈為什麼常見?真正原因是中心極限定理(central limit theorem)。
“多個獨立統計量的和的平均值,符合正態分佈。”
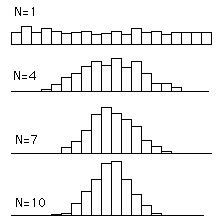
上圖中,隨著統計量個數的增加,它們和的平均值越來越符合正態分佈。
根據中心極限定理,如果一個事物受到多種因素的影響,不管每個因素本身是什麼分佈,它們加總後,結果的平均值就是正態分佈。
舉例來說,人的身高既有先天因素(基因),也有後天因素(營養)。每一種因素對身高的影響都是一個統計量,不管這些統計量本身是什麼分佈,它們和的平均值符合正態分佈。(註意:男性身高和女性身高都是正態分佈,但男女混合人群的身高不是正態分佈。)
許多事物都受到多種因素的影響,這導致了正態分佈的常見。
讀到這裡,讀者可能馬上就會提出一個問題:正態分佈是對稱的(高個子與矮個子的比例相同),但是很多真實世界的分佈是不對稱的。

比如,財富的分佈就是不對稱的,富人的有錢程度(可能比平均值高出上萬倍),遠遠超出窮人的貧窮程度(平均值的十分之一就是赤貧了),即財富分佈曲線有右側的長尾。相比來說,身高的差異就小得多,最高和最矮的人與平均身高的差距,都在30%多。
這是為什麼呢,財富明明也受到多種因素的影響,怎麼就不是正態分佈呢?
原來,正態分佈只適合各種因素累加的情況,如果這些因素不是彼此獨立的,會互相加強影響,那麼就不是正態分佈了。一個人是否能夠掙大錢,由多種因素決定:
家庭
教育
運氣
工作
…
這些因素都不是獨立的,會彼此加強。如果出生在上層家庭,那麼你就有更大的機會接受良好的教育、找到高薪的工作、遇見好機會,反之亦然。也就是說,這不是 1 + 1 = 2 的效果,而是 1 + 1 > 2。
統計學家發現,如果各種因素對結果的影響不是相加,而是相乘,那麼最終結果不是正態分佈,而是對數正態分佈(log normal distribution),即x的對數值log(x)滿足正態分佈。
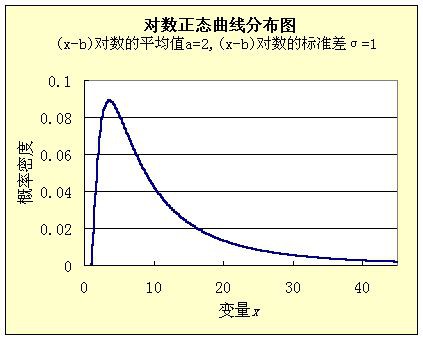
這就是說,財富的對數值滿足正態分佈。如果平均財富是10,000元,那麼1000元~10,000元之間的窮人(比平均值低一個數量級,寬度為9000)與10,000元~100,000元之間的富人(比平均值高一個數量級,寬度為90,000)人數一樣多。因此,財富曲線左側的範圍比較窄,右側出現長尾。
參考連結
Why isn’t everything normally distributed?,by John D. Cook
https://www.johndcook.com/blog/2015/03/09/why-isnt-everything-normally-distributed/
Achievement is not normal, by John D. Cook
https://www.johndcook.com/blog/2015/03/09/why-isnt-everything-normally-distributed/
推薦閱讀
(點選標題可跳轉閱讀)
遊戲主機編年史
影象主題色提取演演算法
推薦系統概述
覺得本文有幫助?請分享給更多人
關註「演演算法愛好者」加星標,修煉程式設計內功
 知識星球
知識星球