知識星球作者丨蘇劍林
單位丨廣州火焰資訊科技有限公司
研究方向丨NLP，神經網路
個人主頁丨kexue.fm
在本文中，我們再次對 Capsule 進行一次分析。
整體上來看，Capsule 演演算法的細節不是很複雜，對照著它的流程把 Capsule 用框架實現它基本是沒問題的。所以，困難的問題是理解 Capsule 究竟做了什麼，以及為什麼要這樣做，尤其是 Dynamic Routing 那幾步。
為什麼我要反覆對 Capsule 進行分析？這絕非單純的“炒冷飯”，而是為了得到對 Capsule 原理的理解。
眾所周知，Capsule 給人的感覺就是“似乎有太多人為約定的內容”，沒有一種“雖然我不懂，但我相信應該就是這樣”的直觀感受。我希望盡可能將 Capsule 的來龍去脈思考清楚，使我們能覺得 Capsule 是一個自然、流暢的模型，甚至對它舉一反三。
在揭開迷霧，來一頓美味的「Capsule」盛宴中，筆者先分析了動態路由的結果，然後指出輸出是輸入的某種聚類，這個“從結果到原因”的過程多多少少有些望文生義的猜測成分。
這次則反過來，直接確認輸出是輸入的聚類，然後反推動態路由應該是怎樣的，其中含糊的成分大大減少。兩篇文章之間有一定的互補作用。
Capsule框架
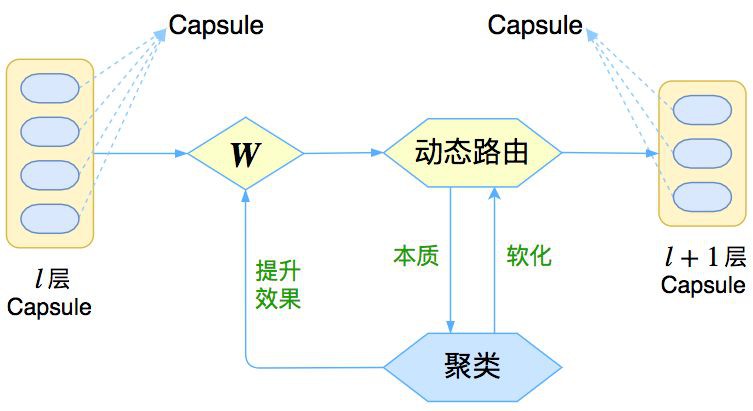
△ 圖1：Capsule框架的簡明示意圖
與其說 Capsule 是一個具體的模型，倒不如說 Capsule 是一個建模的框架，而框架內每個步驟的內容，是可以自己靈活替換的，而 Hinton 所發表的論文，只是一個使用案例。
這是一個怎樣的框架呢？
特徵表達
Capsule 模型中，每個特徵都是用一個向量（即 Capsule，膠囊）來表示的。
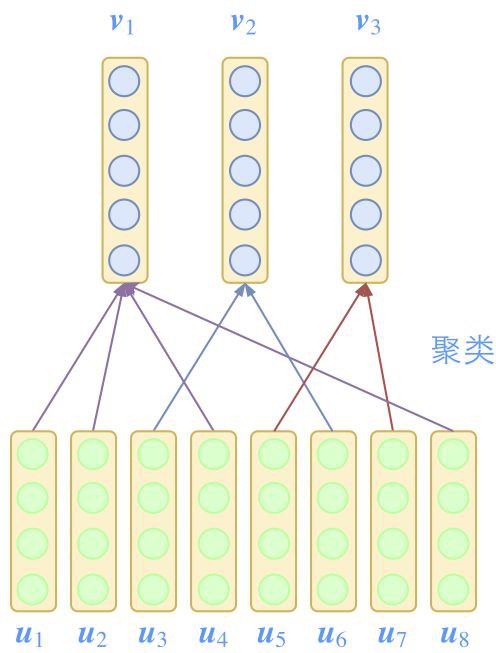
△ 圖2：Capsule的每個特徵都是向量，並且透過聚類來遞進
當然，對於關註新聞的讀者來說，這已經不是什麼新訊息。可能讀者會有疑問：用向量來表示特徵有什麼稀奇的，本來神經網路的特徵輸入不就是一個向量嗎？
原來神經網路（MLP）的每一層輸入是一個向量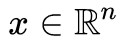
，然後輸出是
，我們就將 x 的每一個分量都看成一個特徵，那麼每個特徵都是標量了。
而所謂的特徵向量化後，那麼每一層的輸入變成了
，然後輸出是
，這時候的輸入 x 也看成是 n 個特徵，但每個特徵都是一個 dx 維向量；輸出 y 則看成是 k 個特徵，每個特徵是一個 dy 維向量。
換一個角度看，其實就是說 MLP 每一層的輸入輸出由單個的向量變成了向量的集合（矩陣）。
或者我們可以將它換一個名稱，叫做“特徵的分散式表示”。也許有讀者看到了“分散式表示”，會想起 NLP 中的詞向量。
沒錯，詞向量一開始確實叫做“分散式表示”（Distributed Representation），而筆者看到 Capsule 的這一特點，第一反應也就是詞向量。
我們可以用詞向量代替 one hot 來表示一個詞，這樣表達的資訊就更為豐富了，而且所有的詞都位於同一向量空間，方便後續處理。
此外，事實上影象中早也有這樣的例子，眾所周知彩色影象一般有 RGB 三個通道，每個通道 256 個選擇，所以一共可以表達 256 的三次方，即 16777216 種顏色（約 1700 萬）。
為什麼不直接用 1700 萬個數字來分別表示這 1700 種顏色，而要分開 3 組，每組 256 個數字呢？
這其實也是一種分散式表示，這樣可以更好地表達色彩的多樣性。比如紅色的相近顏色是什麼色？也許有人說橙色，也有人說紫色，也有可能是粉紅，單一一個數字難以表達多種的相似性，而分組後則可以。
更進一步說，我們在對影象不斷進行摺積操作時，所得結果的通道維度，其實就是影象特徵的一種分散式表示了。
特徵組合
Capsule 的第二個特點，是透過聚類來組合特徵。
組合與表達
透過將底層特徵組合為上層的特徵，是跟我們的認知規律是相符的。在NLP中，我們有“字–>詞–>句–>段”的層層組合；在影象中，我們也有“點–>線–>面–>體”的層層組合。
面對新事物（上層特徵），我們總會將它分解為我們熟悉的一些事物（底層特徵），然後腦海裡將這些事物對映到這個新事物（特徵組合）。
對於我們來說，這個分解和組合的過程，不一定有什麼目的，而只是為了用我們自己的方式去理解這個新事物（在大腦中形成良好的特徵表達）。
這也就能理解 Hinton 詬病深度學習、發展 Capsule 的原因之一了，因為他覺得現在深度學習的模型針對性太強，比如 MNIST 分類模型就只能做單個數字的識別，多個數字的識別就要重新構建資料集、重新設計並訓練模型。
而事實上，我們的根本目的並不是單純地做任務，而是透過任務形成良好的、普適的特徵表達，這樣才有可能形成真正的人工智慧。
特徵間聚類
那麼，怎麼完成這個組合的過程呢？試想一下，兩個字為什麼能成為一個詞，是因為這兩個字經常“扎堆”出現，而且這個“堆”只有它們倆。這就告訴我們，特徵的聚合是因為它們有聚類傾向，所以 Capsule 把聚類演演算法融入到模型中。
要註意，我們以前所說的聚類，都是指樣本間的聚類，比如將 MNIST 的圖片自動聚類成 10 個類別，或者將 Word2Vec 訓練而來的詞向量聚類成若干類，聚類的物件就是一個樣本（輸入）。
而 Capsule 則設想將輸入本身表示為若干個特徵向量，然後對這些向量進行聚類（特徵間的聚類），得到若干中心向量，接著再對這些中心向量聚類，層層遞進，從而完成層層抽象的過程。這是一種特徵間的聚類。
現在問題就來了。既然是聚類，是按照什麼方法來聚類的呢？然後又是怎麼根據這個聚類方法來匯出那個神奇的 Dynamic Routing 的呢？後面我們會從K-Means出發來尋根問底，現在讓我們先把主要思路講完。
特徵顯著性
透過特徵的組合可以得到上層特徵，那如何對比特徵的強弱程度呢？
Capsule 的答案是：模長。這就好比在茫茫向量如何找出“突出”的那個？只需要看看誰更高就行了。因此透過特徵向量的模長來衡量它自己的“突出程度”，顯然也是比較自然的選擇。
此外，一個有界的度量也是我們希望的，因此我們對特徵向量做一個壓縮：
壓縮的方案並不唯一，這裡就不展開了。不過我在實驗過程中，發現將 1 替換為 0.5 能提升效能。
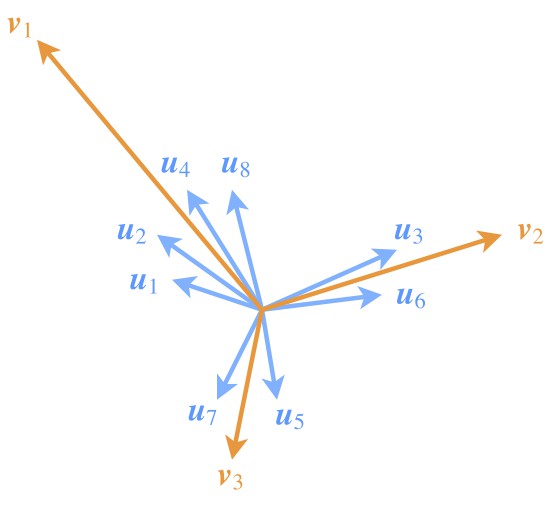
△ 圖3：Capsule透過特徵向量的聚類，來刻畫特徵的組合特性
為了突出模長的這一含義，也需要在設計模型的時候有所配合。如圖，儘管 v1 所代表的類所包含的特徵向量 u1,u2,u4,u8 的模長均比較小，但因為成員多（“小弟多”），因此 v1 的模長也能佔優（“勢力大”）。
這說明，一個類要突出，跟類內向量的數目、每個類內向量本身的模長都有關聯。後面我們也會看到 Capsule 是如何體現這一點的。
K-Means新探
既然本文不斷強調 Capsule 是透過聚類來抽象特徵的，那麼就有必要來細談一下聚類演演算法了。Capsule 所使用的聚類演演算法，其實是 K-Means 的變種。
聚類演演算法有很多，理論上每種聚類演演算法都是可能的，然而要將聚類演演算法嵌入到 Capsule 中，還需要費上一點周折。
聚類標的
K-Means 聚類本質上是一種“中心聚類方法”——聚類就是找類別中心。為了定義中心，我們就需要一個相近程度的度量，常用的是歐氏距離，但這並不是唯一的選擇。
所以這裡我們乾脆在一個更加一般的框架下介紹 K-Means：K-Means 希望把已有的資料 u1,u2,…,un 無監督地劃分為 k 類，聚類的方法是找出 k 個聚類中心 v1,v2,…,vk，使得類內間隔最小：
這裡 d 代表了相近程度的度量，所以這個式子的意思很簡單，就是說每個 ui 只屬於跟它最相近的那一類，然後將所有類內距離加起來，最小化這個類內距離：
顯然，聚類的結果依賴於 d 的具體形式，這其實就告訴我們：無監督學習和有監督學習的差別，在於我們跟模型“交流”的方法不同。
有監督學習中，我們透過標註資料向模型傳達我們的意願；在無監督學習中，我們則透過設計適當的度量 d 來完成這個過程。
求解過程
怎麼去最小化 L 來求出各個中心呢？如果讀者不希望細細瞭解推導過程，可以跳過這一節，直接看下一節。
因為 L 中有 min 這個操作，所以直接求它的梯度會有困難（不是不能求，而是在臨界點附近不好處理），事實上有很多類似的問題沒能得到很好的解決，都是因為它們的 loss 中有 min。
然而，這裡我們可以“軟化”這個 L，使得它可以求導。因為我們有一個很漂亮的公式：
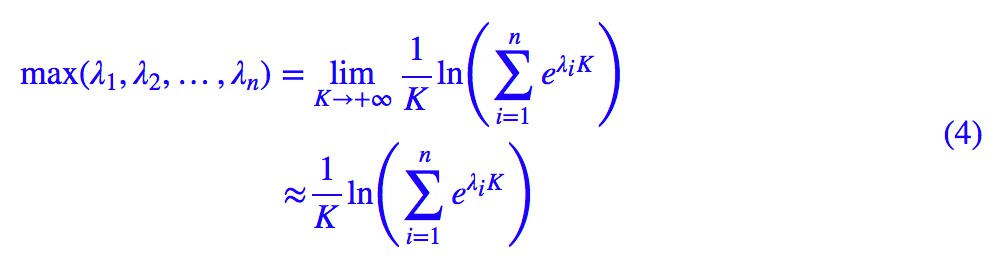
如果取 K=1，顯然括號裡邊就是 softmax 的分母，這也就是 softmax 的由來了——它是“soft”加“max”——“軟的最大值”。
而我們有：
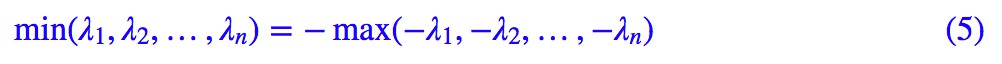
因此我們就得到：
現在這個近似的 loss 在全域性都光滑可導了，因此我們可以嘗試求它的梯度。
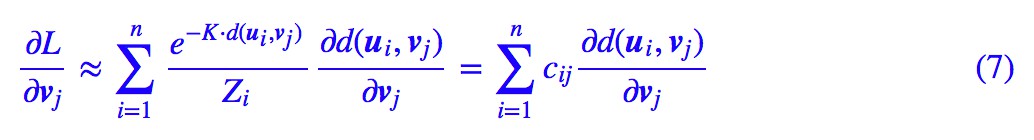
這裡：
我們已經指明瞭是對 j 所在的維度來歸一化。為了求出一個極小值，我們希望讓 ∂L/∂vj=0，但得到的方程並不是簡單可解的。因此，可以引入一個迭代過程，假設
是 vj 的第 r 次迭代的結果，那麼我們可以讓：
如果可以從上述方程解出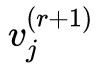
，那麼就可以從中得到一個迭代格式。
歐氏距離
現在就可以把我們選擇的度量代入（8）式進行計算了。我們可以看一個最基本的例子：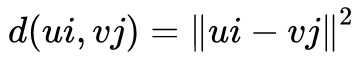
，這時候就有：
從而我們可以解出：
如果取 K→+∞，那麼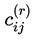
非 0 即 1，所以上式就是說（讀者可以自己證明一下）
是距離最近的那些 ui 的平均值。
這就得到了我們平時說的 K-Means 聚類演演算法。
內積相似度
歐氏距離並不適合用在 Capsule 中，這是因為歐氏距離得到的中心向量是類內的向量的平均，這樣類內向量越多，也不會導致中心向量的模越長，這不滿足我們前面說的“小弟越多，勢力越大”的設計。
什麼距離比較適合呢？在論文 Dynamic Routing Between Capsules 中有一段話：
The initial coupling coefficients are then iteratively refined by measuring the agreement between the current output vjvj of each capsule, jj, in the layer above and the prediction û j|i made by capsule ii.
The agreement is simply the scalar product aij=vj⋅u^j|i …
對應到本文，大概的意思是用內積⟨ui,vj⟩作為相似度的度量，也就是說，d(ui,vj)=−⟨ui,vj⟩。但仔細思考就會發現問題，因為這樣的 d 是無下界的。
無下界的函式我們不能用來做 loss，所以我一直被這裡困惑著。直到有一天，我覺得可以將 vj 先歸一化，然後再算內積，這樣一來實際上是：
現在對於固定的 ui，不管 vj 怎麼變，d(ui,vj) 就有下界了。所以這樣的 d 是可以用來作為 loss，代入（8）式算，最終得到的結果是：
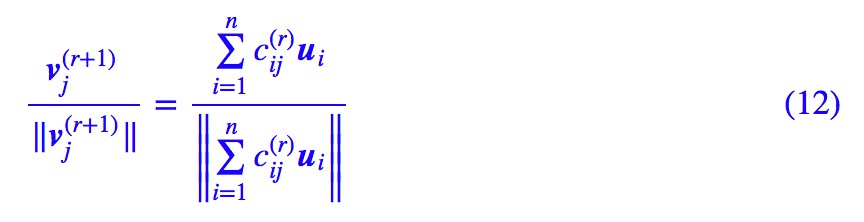
註意這結果只能說明和
的方向是一樣的，但不能說明它們兩個是相等的。然而，我們確實可以簡單地取：
如果取 K→+∞ 的極限，那麼就是說是距離最近的那些 ui 的和。
由於現在是求和，就可以體現出“小弟越多，勢力越大”的特點了。註意，這裡和歐氏距離那都出現了“最近”，兩個最近的含義並不一樣，因為所選用的 d 不一樣。
動態路由
經過漫長的準備，Dynamic Routing 演演算法已經呼之欲出了。
按照第一部分，我們說 Capsule 中每一層是透過特徵間聚類來完成特徵的組合與抽象，聚類需要反覆迭代，是一個隱式的過程。我們需要為每一層找到光滑的、顯式的運算式：
才能完成模型的訓練。動態路由就是透過迭代來寫出這個（近似的）顯式運算式的過程。
基本步驟
假設 Capsule 的輸入特徵分別為 u1,u2,…,un，然後下一層的特徵向量就是 v1,v2,…,vk，它就是前一層 n 個向量聚為 k 類的聚類中心，聚類的度量是前面的歸一化內積，於是我們就可以寫出迭代過程：
這個版本是容易理解，但由於存在 argmax 這個操作，我們用不了梯度下降，而梯度下降是目前求模型其他引數的唯一方法。為瞭解決這個問題，我們只好不取 K→+∞ 的極限，取一個常數 K>0，然後將演演算法變為：
然而這樣又新引入了一個引數 K，咋看上去 K 太大了就梯度消失，K 太小了就不夠準確，很難確定。不過後面我們將會看到，直接讓 K=1 即可，因為 K=1 的解空間已經包含了任意 K 的解。最終我們可以得到：
有意思的是，最後匯出的結果，不僅跟 Hinton 的原始論文 Dynamic Routing Between Capsules 有所出入，跟我前一篇介紹也有出入。
其中，最明顯的差別是在迭代過程中用 vj/‖vj‖ 替換了 squash(vj)，僅在最後輸出時才進行 squash。實驗表明這有助於提升特徵的表達能力，它在我的前一文的數字實驗（單數字訓練，雙數字預測）中，能達到 95% 以上的準確率（原來是 91%）。
三種癥狀
這樣就完了？遠遠還沒有。我們還要解決好幾個問題。
1. 如何做好類別初始化？ 因為聚類結果跟初始化有關，而且好的初始化往往是聚類成功的一大半。現在我們要將聚類這個過程嵌入到模型中，作為模型的一部分，那麼各個
應該怎麼選取呢？
如果同一初始化，那麼無法完成聚類過程；如果隨機初始化，那又不能得到確定的聚類結果，就算類中心向量不變，但是類的順序也可能變化。
2. 如何識別特徵順序？我們知道，聚類的結果跟樣本的順序是無關的，也就是說，如果將輸入向量的順序打亂，聚類的結果還是一樣的。
對於樣本間的聚類，這是一個優點；然而如果是特徵間的聚類，那麼就有可能不妥了，因為不同順序的特徵組合可能代表不同的含義（就好比詞序不同，句子含義也會不同），如果都給出一樣的結果，那麼就喪失了特徵的序資訊了；
3. 如何保證特徵表達能力？動態路由將上層 Capsule 作為底層 Capsule 的聚類結果，每個類可能包含多個特徵向量，但如果僅僅用類中心向量整個類的整體特徵（上層特徵），會不會降低了上層 Capsule 的特徵表達能力？
一個對策
有意思的是，以上三個問題都可以由同一個方法解決：加變換矩陣。
首先，為了模型的簡潔性，我們將所有 ui 的和平均分配到每個類中作為。那怎麼分辨出各個不同的類呢？我們在輸出到每個類之前，給每個類都配一個變換矩陣 Wj，用來分辨不同的類，這時候動態路由變成了：
這就是我前一篇介紹中所說的共享權重版的 Capsule。細細斟酌就會發現，引入訓練矩陣 Wj 是個非常妙的招數，它不僅讓聚類演演算法在同一初始化時仍能分辨出不同的類，而且透過 Wj 可以改變 ui 的維度，從而也就改變了聚類後的中心向量的維度，這樣也就能保證中心向量的特徵表達能力。
此外還有一個好處，那就是⟨Wjui,Kvj⟩=⟨(KWj)ui,vj⟩，也就是說它相當於把前面的引數 K 也包含了，從而我們可以放心設 K=1 而不用擔心準確性不夠——如果有必要，模型會自己去調整 Wj 達到調整 K 的效果。
現在只剩下最後一個問題了：識別輸入特徵的順序。跟識別每一個類一樣，我們也可以給每個輸入都配一個變換矩陣 W̃i，用來分辨不同位置的輸入，這樣一來動態路由變為：
如果覺得這樣太累贅，那麼可以把 WjW̃i 替換成一個整體矩陣 Wji，也就是對每對指標 (i,j) 都配上一個變換矩陣，這樣的好處是整體更簡單明瞭了，缺點是矩陣數目從 n+k 個變成了 nk 個：
這便是全連線版的動態路由。然而並不是每次我們都要分辨不同位置的輸入，對於變長的輸入，我們就很難給每個位置的輸入都分配一個變換矩陣，這時候共享版的動態路由就能派上用場了。總的來說，全連線版和共享版動態路由都有其用武之地。
△ 圖4：Capsule的變換矩陣可能的所在之處
結語
筆者透過這兩篇“浩浩蕩盪”（哆裡哆嗦）的文章，來試圖解讀 Hinton 大力發展的 Capsule 模型，然而作者水平有限，其中不當之處，還請讀者海涵。
個人認為，Capsule 的確是新穎的、有前景的的研究內容。也許它不一定（但也是有可能的）是未來的發展方向，但細細品味它，仍足以讓我們獲益良多。
Hinton 大膽地將聚類的迭代過程融入到神經網路中，因此誕生了 Capsule，那是不是說，可以考慮將其他比較直觀的演演算法也融入到裡邊，從而造就其他有意思的玩意？讓我們拭目以待。
#榜 單 公 布 #
2017年度最值得讀的AI論文 | NLP篇 · 評選結果公佈
2017年度最值得讀的AI論文 | CV篇 · 評選結果公佈
我是彩蛋
解鎖新功能：熱門職位推薦！
PaperWeekly小程式升級啦
今日arXiv√猜你喜歡√熱門職位√
找全職找實習都不是問題
解鎖方式
1. 識別下方二維碼開啟小程式
2. 用PaperWeekly社群賬號進行登陸
3. 登陸後即可解鎖所有功能
職位釋出
請新增小助手微信（pwbot01）進行諮詢
長按識別二維碼，使用小程式
*點選閱讀原文即可註冊
關於PaperWeekly
PaperWeekly 是一個推薦、解讀、討論、報道人工智慧前沿論文成果的學術平臺。如果你研究或從事 AI 領域，歡迎在公眾號後臺點選「交流群」，小助手將把你帶入 PaperWeekly 的交流群裡。
▽ 點選 | 閱讀原文 | 進入作者部落格